推广到n维空间，体积表达式是什么样？

nyy

二维空间，正三角形的体积=sqrt(3)/4*a^2
三维空间，正四面体的体积=sqrt(2)/12*a^3  （a是棱的长度）

推广到n维空间，体积表达式是什么样？

mathe

容易看出n维中，重心将一条高划分为n:1俩部分。而重心到一个n-1维"超面"的投影投影是其重心，
容易看出长度为$\frac{(n)h_n}{n+1}, \frac{h_n}{n+1}, \frac{(n-1)h_{n-1}}n$的三条线段构成直角三角形。

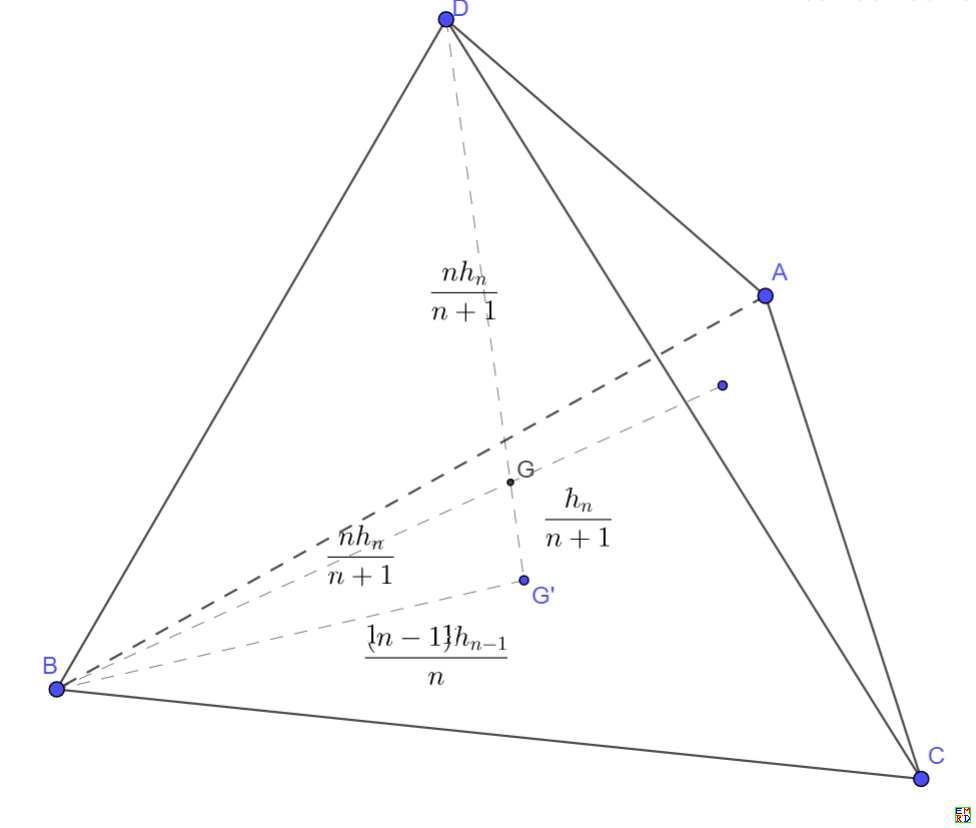
于是我们得到递推式
\(\left(\frac{n*h_n}{n+1}\right)^2= \left(\frac{h_n}{n+1}\right)^2+\left(\frac{(n-1)h_{n-1}}{n}\right)^2\)
即\(h_n^2=\frac{n^2-1}{n^2}h_{n-1}^2\)
而且我们可以看成\(h_1^2=1\),于是得到\(h_n^2=\frac{n+1}{2n}\)
另外\(V_n=\frac{V_{n-1}h_n}n\)，所以我们可以有\(V_n^2=\frac{V_{n-1}^2 h_n^2}{n^2}=\frac{(n+1)V_{n-1}^2}{2n^3}\)，其中\(V_1=1\)
可以得到\(V_n^2 = \frac{(n+1)}{2^{n}n!^2}\)即\(V_n=\frac{\sqrt{n+1}}{2^{n/2}n!}\)
比如n=2,就得到单位边长正三角形面积公式为\(V_2=\frac{\sqrt{3}}4\), n=3就得到单位边长正四面体体积为\(V_3=\frac{\sqrt{2}}{12}\)

nyy

mathe 发表于 2024-4-12 09:22
容易看出n维中，重心将一条高划分为n:1俩部分。而重心到一个n-1维"超面"的投影投影是其重心，
容易看出长度 ...

能用gamma函数写成统一的形式吗？