- 注册时间
- 2016-5-4
- 最后登录
- 1970-1-1
- 威望
- 星
- 金币
- 枚
- 贡献
- 分
- 经验
- 点
- 鲜花
- 朵
- 魅力
- 点
- 上传
- 次
- 下载
- 次
- 积分
- 270
- 在线时间
- 小时
|
 发表于 2023-9-22 14:29:10
来自手机
|
显示全部楼层
发表于 2023-9-22 14:29:10
来自手机
|
显示全部楼层
本帖最后由 yuange1975 于 2023-9-22 20:44 编辑
前天爬山手机上写代码调试出来,今天有空整理了一下。
懒得写分析文章了,代码很简单,有兴趣的自己看代码吧。小小的打一个广告,有兴趣的可以加入我的知识星球《袁哥的技术天地》,主要是网络安全、数学、投资等方面的一些经验的随意分享。
两互相垂直平面切一球,切成四部分,依次体积为abcd。已知abc,求d=?
这题情形现实中还是很常见的,切球形西瓜、土豆等。
就是图1的圆的问题推广成球的问题。球半径R,两垂直平面交点P坐标(R*x,R*y)。
n为精度位数,可以设置成需要的求解精度要求。
求得如图1的数据d=15.2684403090431785。
abcd按逆时针顺序排列,就是分别是坐标体系里的第一二三四象限。
有三个方程:
3(a+b)/(pi*R^3)=y^3-3y+2
3(b+c)/(pi*R^3)=-x^3+3x+2
r=sqrt(1-x*x-y*y)
rx=sqrt(1-x*x)
ry=sqrt(1-y*y)
a=f(x,y)=(2*x*y*r+2*acos(x/rx*y/ry)+(x**3-3*x)*acos(y/rx)+(y**3-3*y)*acos(x/ry)/3*R^3
求d的方程
3(a+b+c+d)=4*pi*R^3
P点坐标(x*R,y*R)(x^2+y^2<=1)切的第一块a块的体积公式f(x,y)。b=f(-x,y)和c=f(-x,-y)、d=f(x,-y)都有这样的公式,但是这个公式太复杂。a+b、b+c可以消去一些复杂项,公式变得非常简单。就取一个复杂的a就行,另外两个用简单的方程。
解这3个方程组得到xyR,带入就得到d=4/3*pi*R^3-(a+b+c)。
Python 代码如下:
- # 两互相直平面切一球,切成四部分,依次体积为abcd。
- # 已知abc,求d=?
- # copy by yuange 2023.9.20
- # n 精度位数
- from mpmath import *
- n=20
- mp.prec=128
- mp.dps=n+1
- rn="\r\n"
- '''
- 3(a+b)/(piR^3)=Y^3-3Y+2
- 3(b+c)/(piR^3)=(-X^3+3X+2)
- Y^3-3Y+2=(a+b)/(b+c)*(-X^3+3X+2)
- a=R^3*vv(x,y)
- '''
- stepn=16
- num=1000
- mpf1=mpf("1")
- mpf0=mpf("0")
- er=pow(mpf("0.1"),n)
-
- def vv(x,y):
- r=sqrt(1-x*x-y*y)
- v0=(2*x*y*r+2*acos(x*y/sqrt(r*r+x*x*y*y))+(x**3-3*x)*acos(y/sqrt(r*r+y*y))+(y**3-3*y)*acos(x/sqrt(r*r+x*x)))/3
- return v0
- def qiu(a,b,c):
- step=mpf1/stepn
- y=0-mpf1
- stop=0
- sign=0
- if c>=b :
- y=mpf0
- stop=1
- fx=lambda x :-x**3+3*x+2-mpf1*(b+c)/(a+b)*(y**3-3*y+2)
- for i in range(num):
- fy=(y**3-3*y+2)*(b+c)/(a+b)-2
- if abs(fy)>2 :
- y+=step
- continue
- x=findroot(fx,0)
- #print(rn,"x,y=",x,y)
- if x*x+y*y > 1+1e-5 :
- y+=step
- if y > 1 :break
- continue
- a1=vv(x,y)
- R1=3*(a+b)/pi/(y**3-3*y+2)
- R2=a/a1
- #print(rn,"R1,R2=",R1,R2,R1-R2,step,a1)
- if abs(R1-R2) < er :
- R=cbrt(R1)
- d=4*pi*R1/3-a-b-c
- #print(rn,"ok!X,Y,R,d=",x*R,y*R,R,d)
- return x,y,R,d
- break
- if (R1-R2)>0 :
- y-=step
- step=step/stepn
- #print(rn,"step=",step)
- continue
- y+=step
- if y>stop+0.1 :
- break
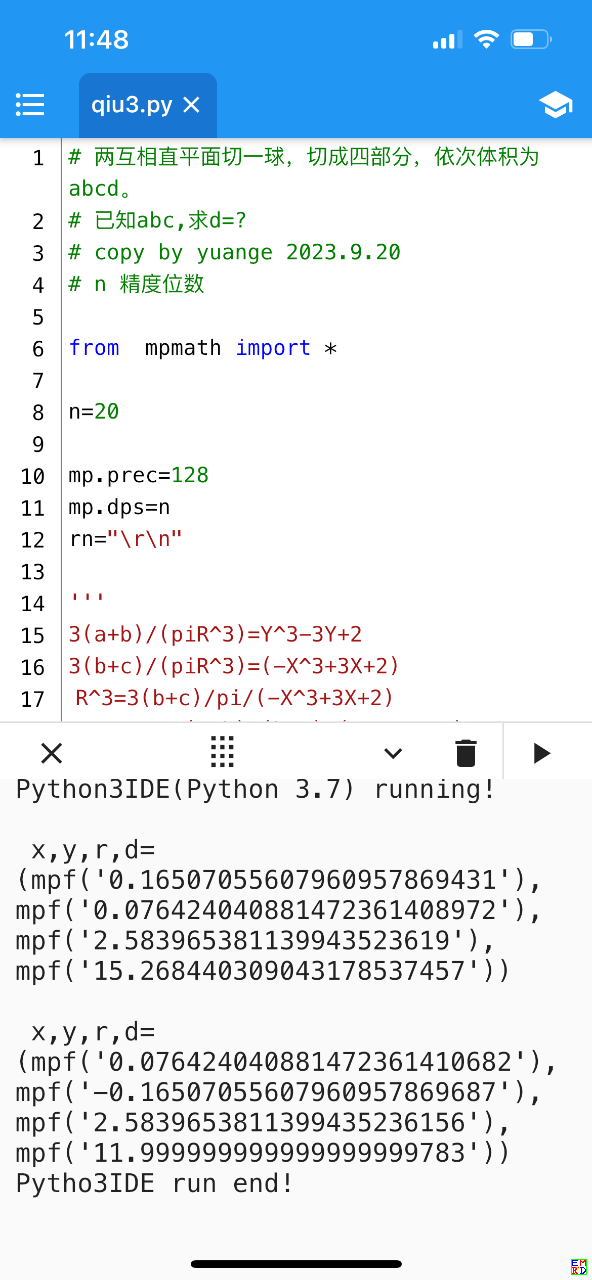
- x,y,r,d=qiu(12,20,25)
- print(rn,"x,y,r,d=",(x,y,r,d))
- x,y,r,d=qiu(20,25,d)
- print(rn,"x,y,r,d=",(x,y,r,d))
|
-
|