- 注册时间
- 2008-11-26
- 最后登录
- 1970-1-1
- 威望
- 星
- 金币
- 枚
- 贡献
- 分
- 经验
- 点
- 鲜花
- 朵
- 魅力
- 点
- 上传
- 次
- 下载
- 次
- 积分
- 149506
- 在线时间
- 小时
|
马上注册,结交更多好友,享用更多功能,让你轻松玩转社区。
您需要 登录 才可以下载或查看,没有账号?欢迎注册
×
- Clear["Global`*"];
- aa=D[ArcTan[x],{x,105}]
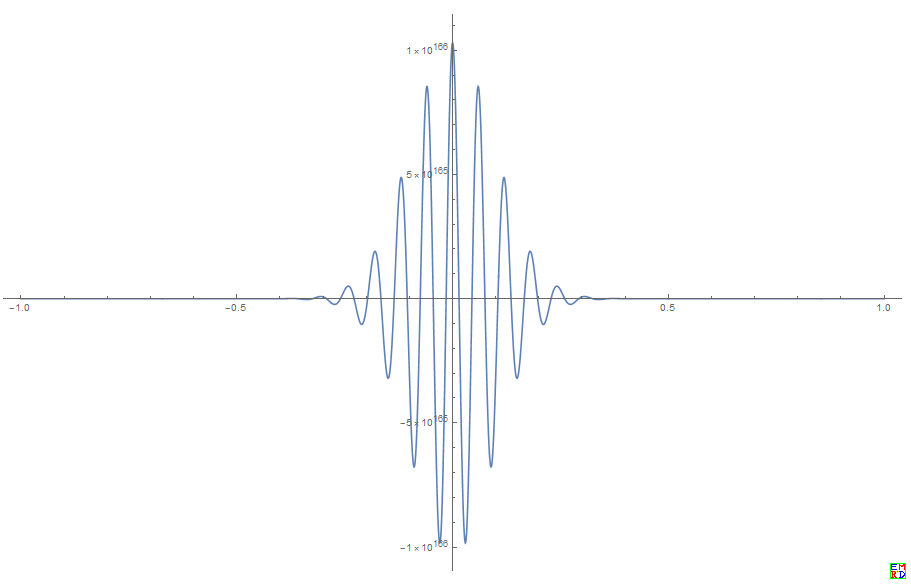
- bb=Plot[aa,{x,-1,1},PlotRange->All]
\[\frac{\pi}{4} = 4 \arctan\frac{1}{5} - \arctan\frac{1}{239}\]
利用马青公式计算圆周率的时候,由于只能利用前n项计算圆周率,后面项舍弃,所以我想利用拉格朗日余项的大小来确定需要计算多少项。
但是拉格朗日余项公式需要利用n阶导数的绝对值在[0,0.2]的大小来估算余项的大小,从而确定计算多少项。
利用上面的mathematica代码,我计算得到。
\[\frac{10299016745145627623848583864765044283053772454999072182325491776887871732475287174542709871683888003235965704141638377695179741979175588724736000000000000000000000000 \left(105 x^{104}-187460 x^{102}+96560646 x^{100}-22760723700 x^{98}+3005047770725 x^{96}-249145778809200 x^{94}+13961746143269400 x^{92}-556608279578340080 x^{90}+16391295291994500150 x^{88}-366934961273420740200 x^{86}+6386415635496918121100 x^{84}-87996224922301409368200 x^{82}+974118209889876601705974 x^{80}-8769839154564131229033840 x^{78}+64866568919103660297508920 x^{76}-397569293375151466339570800 x^{74}+2033777767814932027619660475 x^{72}-8736699116865489516967818780 x^{70}+31680372923769004779995919450 x^{68}-97392563455257480281822813100 x^{66}+254764693428691823420134065975 x^{64}-568776989980335233682159775200 x^{62}+1086421503083650431205014277680 x^{60}-1778877021700334193554926245600 x^{58}+2500411323869602399614194799300 x^{56}-3020104657850343290514399992880 x^{54}+3136262529306125724764953838760 x^{52}-2800460682733954687567898175216 x^{50}+2149476401221237150545535880100 x^{48}-1417071525761283171136975144800 x^{46}+801458485881381465643043319600 x^{44}-388212866177054207116394767200 x^{42}+160697729701174842465007641615 x^{40}-56691193653060324343150592700 x^{38}+16988026060571785171881869850 x^{36}-4306823508313973705547516300 x^{34}+919378990930037765910257475 x^{32}-164328641261729272753689264 x^{30}+24430266216285794138022840 x^{28}-2997286799661158774479920 x^{26}+300653768484529815341350 x^{24}-24384496062806414644200 x^{22}+1577820333475709182860 x^{20}-80135221427528667400 x^{18}+3130921572628162950 x^{16}-91748617512913200 x^{14}+1951641934005400 x^{12}-28848458598960 x^{10}+278818865325 x^8-1609344100 x^6+4780230 x^4-5460 x^2+1\right)}{\left(x^2+1\right)^{105}}\]
(1/((1 + x^2)^105))\
1029901674514562762384858386476504428305377245499907218232549177688787\
1732475287174542709871683888003235965704141638377695179741979175588724\
736000000000000000000000000 (1 - 5460 x^2 + 4780230 x^4 -
1609344100 x^6 + 278818865325 x^8 - 28848458598960 x^10 +
1951641934005400 x^12 - 91748617512913200 x^14 +
3130921572628162950 x^16 - 80135221427528667400 x^18 +
1577820333475709182860 x^20 - 24384496062806414644200 x^22 +
300653768484529815341350 x^24 - 2997286799661158774479920 x^26 +
24430266216285794138022840 x^28 -
164328641261729272753689264 x^30 +
919378990930037765910257475 x^32 -
4306823508313973705547516300 x^34 +
16988026060571785171881869850 x^36 -
56691193653060324343150592700 x^38 +
160697729701174842465007641615 x^40 -
388212866177054207116394767200 x^42 +
801458485881381465643043319600 x^44 -
1417071525761283171136975144800 x^46 +
2149476401221237150545535880100 x^48 -
2800460682733954687567898175216 x^50 +
3136262529306125724764953838760 x^52 -
3020104657850343290514399992880 x^54 +
2500411323869602399614194799300 x^56 -
1778877021700334193554926245600 x^58 +
1086421503083650431205014277680 x^60 -
568776989980335233682159775200 x^62 +
254764693428691823420134065975 x^64 -
97392563455257480281822813100 x^66 +
31680372923769004779995919450 x^68 -
8736699116865489516967818780 x^70 +
2033777767814932027619660475 x^72 -
397569293375151466339570800 x^74 +
64866568919103660297508920 x^76 - 8769839154564131229033840 x^78 +
974118209889876601705974 x^80 - 87996224922301409368200 x^82 +
6386415635496918121100 x^84 - 366934961273420740200 x^86 +
16391295291994500150 x^88 - 556608279578340080 x^90 +
13961746143269400 x^92 - 249145778809200 x^94 +
3005047770725 x^96 - 22760723700 x^98 + 96560646 x^100 -
187460 x^102 + 105 x^104)
根据这个函数的图像,我觉得当求导的阶数越高,然后在[0,1]之间的极值点越多,所以我觉得很难求解出导数在这个区间的极值,但是如果要能证明绝对值的最大值一定在x=0取到的时候,就比较简单了,但是我觉得不是简单的事,
有谁能证明吗?
不一定限于上面代码中的n=105阶导数,有谁能证明吗?或者就给出一个上界也行,不一定是上确界。
|
-

-
|