三、“最后的晚餐”棋不可能有少于15步解法的证明
要证明“最后的晚餐”棋不可能有少于15步解法初看好像不难,只要将所有少于15步的走法都计算一遍,检查是否有结局就可以了。但由于所有少于15步走法约有1千万亿个,而现在一般的计算机每小时能计算处理约10亿个“最后的晚餐”棋的棋局,一台计算机至少连续不断计算100年时间才能得出结论,所以这样直接计算来证明“最后的晚餐”棋不可能有少于15步解法是不现实的。
为了用计算机证明这个问题,本人采用以下两个方法大大减少了 “最后的晚餐”棋的棋局计算:
1.同构法
在给出同构法之前,先给出“最后的晚餐”棋中的几个定义:
按“最后的晚餐”棋规则走完k(k≥0)步后的图形称为棋局,一个棋局可以用一组有序数列(a1,a2,a3,···,a37)表示,其中当交点编号i上有子时ai=1;反之当交点编号i上无子时ai=0。
令Gp={T,T2,T3,T4,S,ST,ST2,ST3},其中T为将棋局绕中心(交点编号19)逆时针旋转90°(交点编号位置不变化)的变换,S为将棋局绕水平中心线(通过交点编号2、36)旋转180°(交点编号位置不变化)的变换。
可以证明,Gp构成棋局变换的对称群。
棋局P与棋局Q称为同构棋局,如果存在g∈Gp,使得P在g的作用下为Q,即g(P)=Q。
举个例子来形象化说明同构棋局(参见图三),若棋局P0为:
P0=(1,1,1,1,1,0,1,1,1,0,0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1)
则与其同构的8个棋局分别为:
P1=(1,1,1,1,1,1,0,1,1,1,1,1,0,1,1,1,1,1,1,1,0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1)
P2=(1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0,0,1,1,1,0,1,1,1,1,1)
P3=(1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0,1,1,1,1,1,1,1,0,1,1,1,1,1,0,1,1,1,1,1,1)
P4=(1,1,1,1,1,0,1,1,1,0,0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1)
P5=(1,1,1,1,1,0,1,1,1,1,1,1,0,0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1)
P6=(1,1,1,1,0,1,1,1,1,1,0,1,1,1,1,1,0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1)
P7=(1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0,0,1,1,1,1,1,1,0,1,1,1,1,1)
P8=(1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0,1,1,1,1,1,0,1,1,1,1,1,0,1,1,1,1)
 由同构棋局的定义及Gp是群,容易证明同构棋局有以下两条性质:
1)若棋局P与棋局Q为同构棋局,则棋局Q与棋局P也为同构棋局。
2)若棋局P与棋局Q为同构棋局,棋局Q与棋局R为同构棋局,则棋局P与棋局R为同构棋局。
由以上两条性质可以推出:若棋局P与棋局Q为同构棋局,且P再走j步不可能到结局,则Q再走j步也不可能到结局。
同构法的过程如下:
a)在每走一步后的所有棋局中,检查是否有同构棋局,如果有同构棋局,则去掉其中的一个棋局,反复这个过程,直到保留下的都是互不同构的棋局。
b)仅在保留下的互不同构的棋局中再可走下一步。
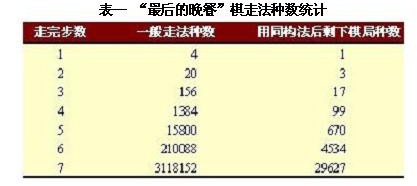
表一给出了第1步到第7步用同构法与不用同构法的走法个数。同构法在实际计算中只用到第7步,因为当大于7步时,内存需要量太大并且计算时间很长,这时再用同构法已没有多大意义了。
用归纳法可以证明,任意一个走完7步后的棋局总与一个用同构法保留下的棋局为同构棋局。所以采用同构法后,“最后的晚餐”棋不可能有少于15步解法可归结为29627个棋局走7步中是否有结局问题。
由同构棋局的定义及Gp是群,容易证明同构棋局有以下两条性质:
1)若棋局P与棋局Q为同构棋局,则棋局Q与棋局P也为同构棋局。
2)若棋局P与棋局Q为同构棋局,棋局Q与棋局R为同构棋局,则棋局P与棋局R为同构棋局。
由以上两条性质可以推出:若棋局P与棋局Q为同构棋局,且P再走j步不可能到结局,则Q再走j步也不可能到结局。
同构法的过程如下:
a)在每走一步后的所有棋局中,检查是否有同构棋局,如果有同构棋局,则去掉其中的一个棋局,反复这个过程,直到保留下的都是互不同构的棋局。
b)仅在保留下的互不同构的棋局中再可走下一步。
表一给出了第1步到第7步用同构法与不用同构法的走法个数。同构法在实际计算中只用到第7步,因为当大于7步时,内存需要量太大并且计算时间很长,这时再用同构法已没有多大意义了。
用归纳法可以证明,任意一个走完7步后的棋局总与一个用同构法保留下的棋局为同构棋局。所以采用同构法后,“最后的晚餐”棋不可能有少于15步解法可归结为29627个棋局走7步中是否有结局问题。
 2.数子法
在给出数子法之前,先给出“可行”棋局的定义:
“最后的晚餐”棋的某一棋局称为“可行”棋局,如果满足以下三个条件:
1)如棋局中共有n个子,则n>12,当n=13时必为结局。
2)如棋局为走第j步过程中的棋局,其中在结局中有子的交点处共有m个子,则j-m<3。
3)如棋局为走完第j步的棋局,其中在结局中有子的交点处共有m个子,则j-m<2。
不难证明,如果“最后的晚餐”棋存在少于15步解法,则解法中的每一步的棋局都是“可行”棋局。
数子法的过程如下:
a)对于“可行”棋局可以继续走下一步。
b)对于非“可行”棋局不再走下一步。
以上是用计算机证明“最后的晚餐”棋最少步数的思路,按此方法本人编制了相应计算程序,在三台普通个人计算机上共耗费约100小时,完成了约4000亿个逻辑判断,最后终于得出:在程序计算中,少于15步的所有走法中没有出现结局,再根据“同构”棋局及“可行”棋局的性质就可得出“最后的晚餐”棋不存在少于15步解法。
在计算证明中还得出了对“最后的晚餐”棋感兴趣者想知道的结论:
在“最后的晚餐”棋的“可行”棋局中,一步最多有138种不同走法;一步中最多可以连跳9次。
以上证明的计算正确性是在计算程序和计算过程没有错误的前提下得出的,对此感兴趣者也可自行编程来验证这个问题。但至少说明了用这种方法证明“最后的晚餐”棋不可能有少于15步的解法是可行的。
《待续3》
2.数子法
在给出数子法之前,先给出“可行”棋局的定义:
“最后的晚餐”棋的某一棋局称为“可行”棋局,如果满足以下三个条件:
1)如棋局中共有n个子,则n>12,当n=13时必为结局。
2)如棋局为走第j步过程中的棋局,其中在结局中有子的交点处共有m个子,则j-m<3。
3)如棋局为走完第j步的棋局,其中在结局中有子的交点处共有m个子,则j-m<2。
不难证明,如果“最后的晚餐”棋存在少于15步解法,则解法中的每一步的棋局都是“可行”棋局。
数子法的过程如下:
a)对于“可行”棋局可以继续走下一步。
b)对于非“可行”棋局不再走下一步。
以上是用计算机证明“最后的晚餐”棋最少步数的思路,按此方法本人编制了相应计算程序,在三台普通个人计算机上共耗费约100小时,完成了约4000亿个逻辑判断,最后终于得出:在程序计算中,少于15步的所有走法中没有出现结局,再根据“同构”棋局及“可行”棋局的性质就可得出“最后的晚餐”棋不存在少于15步解法。
在计算证明中还得出了对“最后的晚餐”棋感兴趣者想知道的结论:
在“最后的晚餐”棋的“可行”棋局中,一步最多有138种不同走法;一步中最多可以连跳9次。
以上证明的计算正确性是在计算程序和计算过程没有错误的前提下得出的,对此感兴趣者也可自行编程来验证这个问题。但至少说明了用这种方法证明“最后的晚餐”棋不可能有少于15步的解法是可行的。
《待续3》 |