KeyTo9无限升级的概率

lsr314 · 发表于 2018-11-16 10:45:15

本帖最后由 lsr314 于 2018-11-16 12:54 编辑

提供一个思路，结论很可能是：KeyTo9可以无限升级的概率是$0$.
考虑经过$n$次升级以后，KeyTo9当前的力量值的期望$E_n$,有递推式$E_0=2,E_(n+1)≈E_n+int_1^(E_n)x*1/x^2dx=E_n+lnE_n.$
近似地有,$E_n≈nlnn.$下一次打得过怪物的概率大约是$1-1/E_n$,于是能无限升级的概率大约是$q=\prod_2^∞(1-1/(nlnn))$
由于和式$\sum_(n=2)^∞1/(nlnn)$是发散的，所以$q=0$.也就是说，KeyTo9可以无限升级的概率是$0$.
$E_n$的递推式不知是否严谨，但是大方向（在渐进的意义上）是没错的，数值验证的结果和渐进式$nlnn$基本一致。
虽然这个结果不够严谨，但是想得到KeyTo9可以无限升级的结论基本上不可能。

mathe · 发表于 2018-11-24 12:16:14

这道题目可以试着用三次样条曲线逼近来求解，
设$\widehat{f_n}(x)$根据函数取值被均分为$N$份，其中又$\widehat{f_n}(x_{n,h})=\frac h N, 0\le h\le N-1, x_{n,0}=1, t_{n,h}=\widehat{f_n}'(x_{n,h})$
由于对于每个分段$x_{n,h}\le x\le x_{n,h+1}$,我们已经知道两个端点函数和其一阶导数的取值，可以唯一确定一个三次函数$\widehat{f_n}(x)=a_{n,h}+b_{n,h}x+c_{n,h}x^2+d_{n,h}x^3, x_{n,h}\le x\le x_{n,h+1}$，其中唯一问题在于最后一段区间$(x_{n,N-1},\infty)$,我们可以假设这段区间上函数取值形如$1-\frac1{u_n+v_n x}$,利用函数在$x_{n,N-1}$处的取值和一阶导数取值可以唯一确定参数$u_n,v_n$
然后利用积分定义容易计算出$\widehat{f_{n+1}}(x_{n,h})$，由此可以确定每个$x_{n+1,h}$所落的区间，由于每个区间里是一个三次函数，解超越方程$\widehat{f_{n+1}}(x_{n+1,h})=\frac h N$可以求得$x_{n+1,h}$。
下面我们还需要计算$\widehat{f_{n+1}}'(x_{n+1,h})$,由于$\widehat{f_{n+1}}(x)=\int_1^x \frac{\widehat{f_n}(x+t)}{t^2}dt$,两边求导得到$\widehat{f_{n+1}}’(x)=\frac{\widehat{f_n}(2x)}{x^2}+\int_1^x \frac{\widehat{f_n}'(x+t)}{t^2}dt$,由此就可以计算出$\widehat{f_{n+1}}'(x_{n+1,h})$
反复迭代上面过程，直到$(x_{n+1,h})$几乎不发生变化，就得到收敛的结果。如果迭代一直无法收敛，说明无解，这时对于给定的$h>0$有,$\lim_{n->\infty} x_{n,h}=\infty$

这个算法中，计算$a_{n,h}, b_{n,h}, c_{n,h}, d_{n,h}$需要解一个四元一次方程组，确定$u_n,v_n$更简单，解二元一次方程组。
其中解方程$\widehat{f_{n+1}}(x_{n+1,h})=\frac h N$是一个超越方程，由于单调，二分法即可，但是这部分计算量有点大
而计算牵涉到的各个定积分，只有最后一个无穷大的区间比较麻烦,我们需要事先推导公式
$\int \frac{dx}{x^2(u+vx)}=\frac{u+vx\ln(x)-vx\ln(u+vx)}{u^2x}$和$\int \frac{dx}{x^2(u+vx)^2}=-\frac{\frac{uv}{u+vx}+\frac u x-2v\ln(u+vx)+2v\ln(x)}{u^3}$

KeyTo9_Fans · 发表于 2018-12-16 14:31:37

我用C++写了随机抽样和等间距抽样程序，各跑了$1$天，结果如下：

其中标红的部分表示这些数字与准确值不符。

#####

根据以上结果，我的结论是：

—————————————————————————————————
在计算量相同的前提下，等间距抽样比随机抽样的计算结果更准确。
—————————————————————————————————

因此我接下来将会长时间运行等间距抽样程序，计算更大的$n$的近似解。

（之前已经运行了一段时间，但是很不幸实验室停电，我的程序又没有断点续跑功能，所以只好从头开始运行）

请大家静候佳音~

#####

wayne更新了他的计算结果，这是更新之后的表格：

根据以上结果，我的结论是：

————————————————————————
在计算量相同的前提下，wayne的计算结果更准确。
————————————————————————

不知道wayne用的是什么算法呢？

精度如此之高，很想学习一下呀~

我的初步猜测是：

wayne先求出准确值的表达式，然后以浮点运算的精度对该表达式进行求值。

.·.·. · 发表于 2018-12-16 20:33:26

KeyTo9_Fans 发表于 2018-12-16 14:31
我用C++写了随机抽样和等间距抽样程序，各跑了$1$天，结果如下：

听说有个叫Antithetic variable的方法
其实大家都知道等间距抽样是好的
但没人知道等间距抽样产生的误差究竟有多大
大家都知道随机不好，
但是大家可以通过随机数据的方差来估计我们的估计误差

Antithetic variable的想法是把这两个东西结合，一方面借用等间距抽样的精度，一方面加入随机抽样的随机性

做法大约是，对$X~F^{-1}(u_1,u_2,u_3,...)$，生成一个对偶变量$X'~F^{-1}(1-u_1,1-u_2,1-u_3,...)$
理论上，如果$X$跟$X'$的相关系数小于0，这样是可以减小误差的
……
具体实现……我只做过最基本的练习题
仅供参考

KeyTo9_Fans · 发表于 2019-1-23 00:46:17

运行时间够久了，见好就收~

我们先来看看随机抽样的结果（然后再看等间距抽样的结果）：

$K29$打$65$只怪$2^34$次，求得存活概率如下：

#include<cmath>
#include<cstdio>
//K29打65只怪2^34次，求得存活概率如下：
double a[66]={
1.0000000000000000,//打0只怪活下来的概率
0.5000000000000000,//打1只怪活下来的概率
0.3513662144559050,//打2只怪活下来的概率
0.2815932136360760,//打3只怪活下来的概率
0.2411939870610670,//打4只怪活下来的概率
0.2147788174076160,//打5只怪活下来的概率
0.1960844954887230,//打6只怪活下来的概率
0.1821000514218010,//打7只怪活下来的概率
0.1712025004164640,//打8只怪活下来的概率
0.1624406088519320,//打9只怪活下来的概率
0.1552199392076540,//... ...
0.1491497625889210,//依次类推
0.1439625207812350,
0.1394686720757390,
0.1355300925893690,
0.1320436452922420,
0.1289307025903360,
0.1261302243508660,
0.1235940617072260,
0.1212836967574740,
0.1191679256057280,
0.1172211841158430,
0.1154223169766410,
0.1137536521266190,
0.1122003071339890,
0.1107496512486020,
0.1093908885908010,
0.1081147336432270,
0.1069131496347130,
0.1057791462666320,
0.1047066098055320,
0.1036901669383610,
0.1027250761863060,
0.1018071345305470,
0.1009326024326260,
0.1000981399239770,
0.0993007552925089,
0.0985377579887405,
0.0978067226882315,
0.0971054555833467,
0.0964319675118892,
0.0957844501656179,
0.0951612551987818,
0.0945608768872055,
0.0939819361677082,
0.0934231677708489,
0.0928834082812828,
0.0923615863941826,
0.0918567135572522,
0.0913678756458316,
0.0908942256862503,
0.0904349785084306,
0.0899894045116523,
0.0895568245676279,
0.0891366064208952,
0.0887281593404700,
0.0883309318481240,
0.0879444083041124,
0.0875681055585488,
0.0872015702317939,
0.0868443768406531,
0.0864961255573120,
0.0861564401382168,
0.0858249661582232,
0.0855013695008716,
0.0851853349845766//打65只怪活下来的概率
},b[66];
int main()
{
//根据前65只怪的存活概率，用如下方法拟合数据：
for(int i=0;i<66;i++)
printf("%lf\n",exp(5/a[i]/13));
return 0;
}
/*
拟合结果如下：
1.469049
2.158106
2.988072
3.919071
4.926510
5.993952
7.109826
8.265665
9.455082
10.673129
11.915899
13.180249
14.463605
15.763842
17.079171
18.408082
19.749281
21.101655
22.464235
23.836174
25.216728
26.605239
28.001121
29.403849
30.812955
32.228014
33.648644
35.074497
36.505258
37.940638
39.380370
40.824214
42.271945
43.723356
45.178258
46.636474
48.097839
49.562202
51.029420
52.499361
53.971899
55.446918
56.924310
58.403970
59.885803
61.369719
62.855633
64.343464
65.833135
67.324574
68.817712
70.312484
71.808830
73.306690
74.806009
76.306737
77.808821
79.312215
80.816871
82.322747
83.829802
85.337997
86.847291
88.357651
89.869040
91.381425
--------------------------------
Process exited after 0.4522 seconds with return value 0
请按任意键继续. . .
*/

复制代码

也就是说，$K29$打了$i$只怪之后，还活着的概率记为$a(i)$，

那么$e^{5/{13a(i)}}$是一个公差约为$1.5~1.6$的等差数列。

#####

我们还可以继续“玩玩”这个“等差数列”，玩法如下。

首先相邻两项作差，得到具体的“公差”，如下所示：

0.689056
0.829966
0.930999
1.007440
1.067442
1.115874
1.155839
1.189417
1.218047
1.242770
1.264349
1.283357
1.300237
1.315329
1.328911
1.341199
1.352373
1.362580
1.371939
1.380554
1.388511
1.395881
1.402729
1.409106
1.415059
1.420630
1.425853
1.430761
1.435380
1.439733
1.443844
1.447731
1.451411
1.454902
1.458216
1.461365
1.464363
1.467218
1.469940
1.472538
1.475019
1.477391
1.479660
1.481833
1.483916
1.485914
1.487831
1.489671
1.491438
1.493138
1.494773
1.496345
1.497861
1.499319
1.500727
1.502085
1.503393
1.504656
1.505876
1.507055
1.508194
1.509295
1.510359
1.511389
1.512385

复制代码

所以最终的“公差”确实是$1.5~1.6$之间。

然后再相邻两项作差，得到“零”数列：

0.140910
0.101033
0.076440
0.060002
0.048432
0.039965
0.033577
0.028630
0.024723
0.021579
0.019007
0.016880
0.015093
0.013581
0.012289
0.011174
0.010206
0.009360
0.008615
0.007957
0.007370
0.006847
0.006377
0.005953
0.005571
0.005223
0.004908
0.004618
0.004353
0.004111
0.003887
0.003681
0.003490
0.003314
0.003149
0.002998
0.002855
0.002722
0.002598
0.002481
0.002372
0.002269
0.002173
0.002083
0.001998
0.001917
0.001840
0.001767
0.001700
0.001634
0.001573
0.001515
0.001459
0.001408
0.001358
0.001309
0.001263
0.001220
0.001179
0.001139
0.001101
0.001065
0.001030
0.000996

复制代码

但这个数列只是趋于零而已，不是真正的“零”数列，

因此我们可以对这个数列的每一项求个倒数，结果如下：

7.0967
9.8978
13.0821
16.6660
20.6475
25.0216
29.7821
34.9279
40.4478
46.3406
52.6111
59.2425
66.2571
73.6308
81.3754
89.4931
97.9794
106.8422
116.0739
125.6790
135.6857
146.0396
156.8104
167.9741
179.5053
191.4649
203.7347
216.5268
229.7178
243.2414
257.2820
271.6839
286.5231
301.7067
317.5212
333.5847
350.2832
367.3291
384.9104
403.0506
421.6116
440.7406
460.1617
480.1155
500.4837
521.6662
543.5428
565.8467
588.2837
611.8185
635.7909
659.9431
685.5477
710.3810
736.5950
764.0615
791.8608
819.5495
848.3488
878.1051
908.4435
939.3187
971.1089
1004.3377

复制代码

未完待续……

#####

对不起，我的拟合方法有误，最终没能成功拟合这批数据

等我找到bug以后，再重新拟合一次，请大家静候佳音~

KeyTo9_Fans · 发表于 2019-1-23 05:15:51

虽然拟合失败，但是我敢肯定，$11#$（$11$楼） lsr314 的猜想是对的！

因为根据楼上（$15$楼）的数据拟合表达式，

如果$e^{x/{a(i)}}$（Fans硬说$x$是$5/13$，其实不是，是Fans猜错了）真的是一个递增的“等差”数列的话，

那么当$i->\infty$时，我们有$e^{x/{a(i)}}=ki+l+o(1)$（常数$k>0$，常数$l=?$待定，$o(1)$是无穷小量），

等式两边取对数，也就是$x/{a(i)}=ln(ki+l+o(1))$，

等式两边乘上$a(i)$，也就是$x=a(i)ln(ki+l+o(1))$，

注意：我们现在要的是$a(i)$，不是$x$，因此上式还要重新写一下（等式两边除下$ln(ki+l+o(1))$），最终写成：

$x/{ln(ki+l+o(1))}=a(i)$

所以当$i->\infty$时，把$\infty$代入上式，得到$a(i)$的极限值是$x/{ln(k\infty+l+o(1))}=0$。

所以 lsr314 猜想正确！加$5$分（威望$+5$，金币$+5$，贡献$+5$，经验$+5$，鲜花$+5$）~

#####

我这还有更多的数据证实这一猜想：

$1$、$K29$打$2^20$只怪$2^22$次的结果如下：

$(1)$、$a(1024)\approx 0.05234$，$1024$就是$2^10$

$(2)$、$a(1048576)\approx 0.02771$，$1048576$就是$2^20$

$2$、$K29$打$2^31$只怪（$2147483648$只怪）$27647$次的结果如下：

27647 //K29一共玩了27647局打怪游戏
0 522 //有522局没死，存活率为522/27647=0.01888...
1 13787 //有13787局被第1只怪打死了，死亡率为13787/27647=0.49867978...
2 4026 //有4026局被第2只怪打死了，死亡率为4026/27647=0.145621586...
3 1982 //……
4 1095 //依次类推~
5 772
6 504
7 405
8 323
9 231
10 204
11 195
12 151
13 124
14 142
15 92
16 84
17 61
18 74
19 59
20 56
21 51
22 44
23 46
24 37
25 32
26 44
27 34
28 40
29 30
30 24
31 37
32 23
（中间省略1331行……）
532168159 1
561727309 1
621241415 1
674399774 1
678850449 1
691751747 1
705548945 1
755139105 1
803611478 1
818034077 1
826452865 1
846223733 1
927544180 1
1020773376 1
1117344357 1
1186318796 1
1234066443 1
1276775823 1
1298175312 1
1305349955 1
1308995527 1
1345644892 1
1368593503 1
1437321579 1
1491328979 1
1552309585 1
1608395272 1
1624049067 1
1694713319 1
1937987860 1
2055735143 1 //运气最差的1次死在第2055735143个怪上

复制代码

想知道上述代码的中间部分是什么样子的吗？

那就下载这个附件看看完整的版本吧~

k29_2.txt (11.89 KB, 下载次数: 0)

KeyTo9_Fans · 发表于 2019-1-23 07:14:59

上天给了Fans一次猜$x$的机会，

但是Fans没有珍惜，直到剧情编不下去了，才后悔不已。

如果上天再给Fans一次机会，

那么Fans会毫不犹豫地把憋了很久的心里话大声地说出来：$x=2/5=0.4$！！！

上天让Fans为自己说的话负责到底，

Fans说：不行啊，我先负责$1$万年再说吧~

#####

玩笑开到这，已经够了。我们推倒重来吧。

#include<cmath>
#include<cstdio>
//K29打65只怪2^34次，求得存活概率如下：
double a[66]={
1.0000000000000000,//打0只怪活下来的概率
0.5000000000000000,//打1只怪活下来的概率
0.3513662144559050,//打2只怪活下来的概率
0.2815932136360760,//打3只怪活下来的概率
0.2411939870610670,//打4只怪活下来的概率
0.2147788174076160,//打5只怪活下来的概率
0.1960844954887230,//打6只怪活下来的概率
0.1821000514218010,//打7只怪活下来的概率
0.1712025004164640,//打8只怪活下来的概率
0.1624406088519320,//打9只怪活下来的概率
0.1552199392076540,//... ...
0.1491497625889210,//依次类推
0.1439625207812350,
0.1394686720757390,
0.1355300925893690,
0.1320436452922420,
0.1289307025903360,
0.1261302243508660,
0.1235940617072260,
0.1212836967574740,
0.1191679256057280,
0.1172211841158430,
0.1154223169766410,
0.1137536521266190,
0.1122003071339890,
0.1107496512486020,
0.1093908885908010,
0.1081147336432270,
0.1069131496347130,
0.1057791462666320,
0.1047066098055320,
0.1036901669383610,
0.1027250761863060,
0.1018071345305470,
0.1009326024326260,
0.1000981399239770,
0.0993007552925089,
0.0985377579887405,
0.0978067226882315,
0.0971054555833467,
0.0964319675118892,
0.0957844501656179,
0.0951612551987818,
0.0945608768872055,
0.0939819361677082,
0.0934231677708489,
0.0928834082812828,
0.0923615863941826,
0.0918567135572522,
0.0913678756458316,
0.0908942256862503,
0.0904349785084306,
0.0899894045116523,
0.0895568245676279,
0.0891366064208952,
0.0887281593404700,
0.0883309318481240,
0.0879444083041124,
0.0875681055585488,
0.0872015702317939,
0.0868443768406531,
0.0864961255573120,
0.0861564401382168,
0.0858249661582232,
0.0855013695008716,
0.0851853349845766//打65只怪活下来的概率
},b[66];
int main()
{
//根据前65只怪的存活概率，用如下方法拟合数据：
for(int i=0;i<66;i++)
printf("%lf\n",exp(2/a[i]/5));
return 0;
}
/*
拟合结果如下：
1.491825
2.225541
3.121811
4.139143
5.250987
6.439050
7.690124
8.994333
10.344081
11.733388
13.157455
14.612366
16.094876
17.602265
19.132225
20.682779
22.252220
23.839063
25.442002
27.059889
28.691700
30.336527
31.993550
33.662034
35.341313
37.030782
38.729891
40.438134
42.155053
43.880221
45.613247
47.353769
49.101450
50.855980
52.617070
54.384449
56.157865
57.937082
59.721879
61.512046
63.307390
65.107723
66.912874
68.722676
70.536975
72.355625
74.178488
76.005430
77.836325
79.671053
81.509501
83.351561
85.197129
87.046108
88.898401
90.753920
92.612581
94.474299
96.338995
98.206594
100.077024
101.950214
103.826097
105.704610
107.585689
109.469275
--------------------------------
Process exited after 0.6761 seconds with return value 0
请按任意键继续. . .
*/

复制代码

需要注意的是，上述代码从第$79$行开始，做了一些改动（具体什么改动？其实就是开头那段玩笑，把$5/13$改成$2/5$了~）。

现在我要为自己说的话负责到底：

上述代码表明，$e^{2/{5a(i)}}$“像”一个等差数列。

怎么像呢？那就准确地说：$e^{2/{5a(i)}}$是一个等差数列与一个无穷小量的和。

我们首先差分一下，得到等差数列的公差与一个无穷小量的和：

0.733716
0.896270
1.017332
1.111844
1.188063
1.251074
1.304208
1.349749
1.389307
1.424067
1.454911
1.482510
1.507389
1.529959
1.550554
1.569442
1.586842
1.602940
1.617886
1.631812
1.644827
1.657023
1.668484
1.679279
1.689469
1.699108
1.708243
1.716919
1.725168
1.733025
1.740522
1.747682
1.754530
1.761089
1.767379
1.773416
1.779217
1.784796
1.790168
1.795343
1.800334
1.805150
1.809802
1.814299
1.818650
1.822862
1.826942
1.830895
1.834728
1.838449
1.842060
1.845568
1.848978
1.852293
1.855520
1.858661
1.861718
1.864696
1.867599
1.870430
1.873190
1.875883
1.878513
1.881080
1.883586

复制代码

再差分一次，就没有公差了，就只剩下一个无穷小量了，结果如下：

0.162554
0.121061
0.094513
0.076219
0.063011
0.053135
0.045540
0.039558
0.034760
0.030844
0.027598
0.024880
0.022570
0.020595
0.018888
0.017401
0.016097
0.014947
0.013926
0.013015
0.012196
0.011461
0.010795
0.010190
0.009639
0.009135
0.008675
0.008249
0.007857
0.007496
0.007160
0.006849
0.006559
0.006290
0.006036
0.005801
0.005579
0.005371
0.005176
0.004991
0.004817
0.004652
0.004497
0.004351
0.004212
0.004080
0.003953
0.003833
0.003721
0.003611
0.003508
0.003410
0.003315
0.003227
0.003141
0.003057
0.002978
0.002903
0.002831
0.002761
0.002693
0.002629
0.002567
0.002506

复制代码

经过仔细观察，Fans认为：这个无穷小量很可能是某个$3$次函数的倒数，

所以接下来把这个数列倒一下，变成一个$3$次的函数，结果如下：

6.1518
8.2603
10.5806
13.1202
15.8703
18.8201
21.9587
25.2791
28.7686
32.4210
36.2340
40.1933
44.3065
48.5563
52.9448
57.4688
62.1223
66.9052
71.8103
76.8361
81.9914
87.2492
92.6360
98.1379
103.7414
109.4678
115.2677
121.2200
127.2734
133.4011
139.6673
146.0128
152.4617
158.9797
165.6602
172.3730
179.2416
186.1699
193.2148
200.3794
207.6184
214.9729
222.3598
229.8469
237.3982
245.1207
252.9752
260.8870
268.7790
276.8974
285.0685
293.2282
301.6832
309.8970
318.3804
327.0922
335.8168
344.4576
353.2829
362.2523
371.2816
380.3596
389.5607
398.9827

复制代码

上次的剧情就编到这，Fans就编不下去了。

这次Fans把$x$的值改过来了，所以剧情可以继续了~

因为是$3$次函数，所以接下来做个开立方运算，

开了立方之后，这个函数就变成$1$次函数了，结果如下：

1.832317
2.021458
2.195348
2.358558
2.513013
2.659953
2.800285
2.934859
3.064122
3.188665
3.309065
3.425453
3.538527
3.648228
3.754981
3.859023
3.960492
4.059632
4.156510
4.251300
4.344330
4.435275
4.524736
4.612598
4.698768
4.783680
4.866715
4.949083
5.030130
5.109595
5.188378
5.265791
5.342201
5.417271
5.492112
5.565315
5.638275
5.710005
5.781140
5.851731
5.921367
5.990474
6.058318
6.125566
6.191927
6.258352
6.324497
6.389754
6.453546
6.517879
6.581371
6.643576
6.706826
6.767150
6.828345
6.890066
6.950789
7.009901
7.069264
7.128591
7.187334
7.245440
7.303399
7.361811

复制代码

因为是$1$次函数，所以可以把这个函数看成一个等差数列与一个无穷小量的和。

于是接下来差分一下，看看这个等差数列的公差到底是多少：

0.189141
0.173890
0.163209
0.154455
0.146940
0.140332
0.134575
0.129263
0.124542
0.120400
0.116389
0.113073
0.109701
0.106753
0.104042
0.101469
0.099140
0.096878
0.094790
0.093030
0.090945
0.089461
0.087862
0.086171
0.084911
0.083035
0.082368
0.081047
0.079465
0.078783
0.077413
0.076410
0.075070
0.074841
0.073203
0.072960
0.071730
0.071135
0.070591
0.069636
0.069108
0.067844
0.067248
0.066361
0.066425
0.066145
0.065257
0.063792
0.064333
0.063493
0.062204
0.063250
0.060323
0.061195
0.061721
0.060723
0.059112
0.059363
0.059327
0.058742
0.058107
0.057959
0.058412

复制代码

这样就很清楚了，这个等差数列的公差介于$0.05$到$0.06$之间。

如果再差分一次，那么这个等差数列就连公差都抵消掉了，就只剩下一个无穷小量了。

所以我们再来差分一下，看看这个无穷小量到底是个什么东西：

-0.01525097
-0.01068094
-0.00875411
-0.00751544
-0.00660746
-0.00575766
-0.00531161
-0.00472049
-0.00414279
-0.00401098
-0.00331540
-0.00337213
-0.00294795
-0.00271077
-0.00257343
-0.00232920
-0.00226204
-0.00208770
-0.00176001
-0.00208529
-0.00148385
-0.00159924
-0.00169120
-0.00125916
-0.00187625
-0.00066710
-0.00132092
-0.00158207
-0.00068221
-0.00136978
-0.00100261
-0.00134044
-0.00022892
-0.00163824
-0.00024305
-0.00122928
-0.00059582
-0.00054408
-0.00095459
-0.00052825
-0.00126385
-0.00059620
-0.00088675
0.00006387
-0.00027943
-0.00088850
-0.00146457
0.00054019
-0.00084002
-0.00128805
0.00104600
-0.00292698
0.00087170
0.00052620
-0.00099837
-0.00161092
0.00025092
-0.00003598
-0.00058464
-0.00063570
-0.00014767
0.00045267

复制代码

这个无穷小量看起来是一个$2$次函数的倒数，

可惜这个函数倒不回来，因为函数值有正有负的，硬倒回来就倒坏了。

我接下来要好好地护着这个函数，不能把它玩坏了……

……怎样才能不被玩坏，又能获得它的近似表达式呢？

——我想到了作图。

那就先把图作出来，看看是啥东西再说：

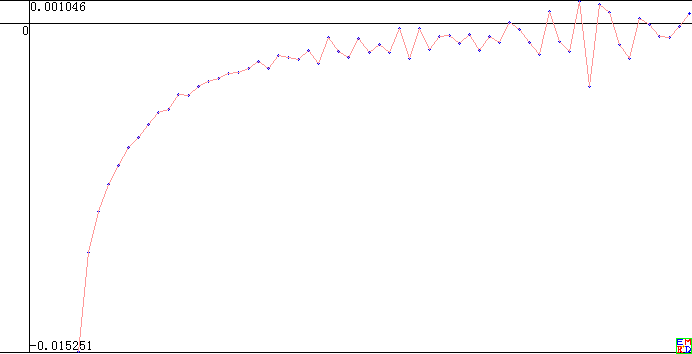
图作出来了，确实是个无穷小量，因为它的极限确实是趋于$0$的，

只是这个函数“抖”得太厉害了。

——为什么会“抖”得这么厉害呢？

因为这是随机取样$2^34$次的计算结果呀~ 有抽样误差在呀~

抽样误差本来是很小很小的，

但是经过一系列变换之后，这个误差越来越大了~

最后大到导致整个【看起来像$2$次函数的倒数】的函数都倒不回去了，无法继续做变换了~

那接下来该怎么办呢？

像这种抖得这么利害的函数，我能想到的唯一办法就是上工具。

有一个叫做【Curve Expert】的神奇工具，你给他一堆散点，他就可以给你一个函数。

（不管你给他的点再散再乱，他都可以给你整个函数出来~）

于是我就把这些【看起来像$2$次函数的倒数的散点】的相反数给他了。

不出所料，他给了我一个函数，说【这个函数是所有函数中拟合得最好的一个函数】：

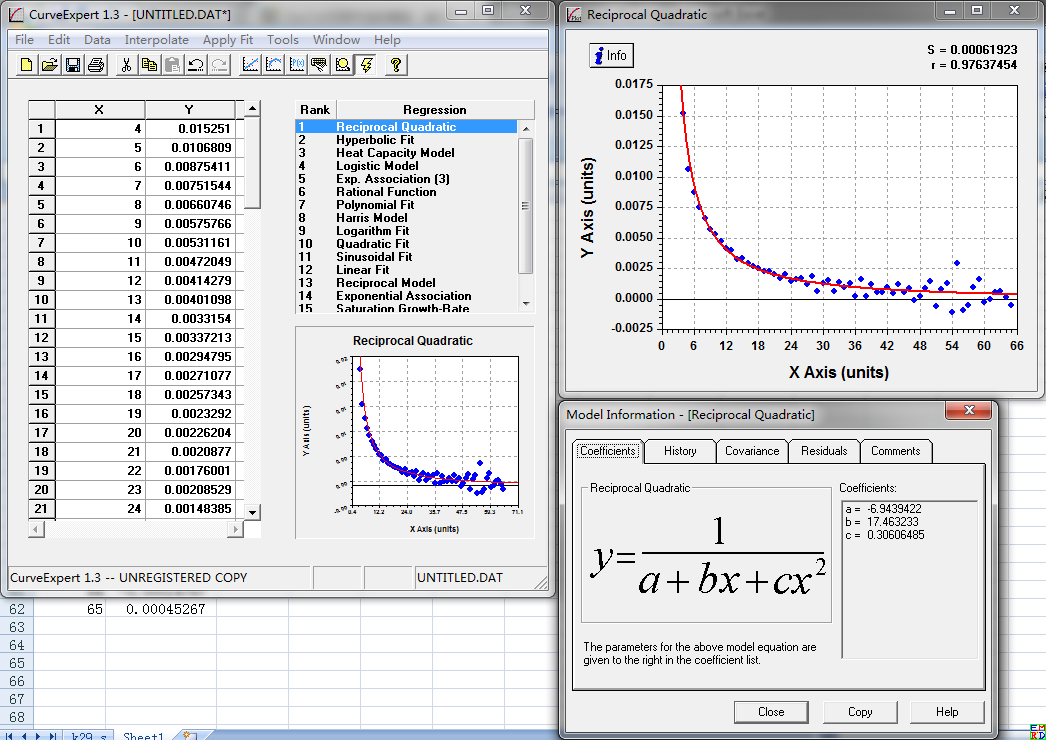
我看了一下，这个函数确实是【$2$次函数的倒数】。

有了这个函数，我就可以预测$i>65$的函数值，然后反推回去，得到$i>65$时的$a(i)$的值。

#####

接下来，见证奇迹的时刻到了。

我们把反推回去的$a(i)$的值与之前所列的值比较一下，看看是否一致：

$(1)$、$a(2^10)\approx 0.05234$：反推回去的$a(2^10)=0.052336710482$，一致！

$(2)$、$a(2^20)\approx 0.02771$：反推回去的$a(2^20)=0.027378206249$，糟糕，不一致……

$(3)$、$a(2^31)\approx 0.01888$：反推回去的$a(2^31)=0.017989797245$，糟糕，这个也不一致……

拟合还是不成功，还得重来……

KeyTo9_Fans · 发表于 2019-1-23 07:26:48

再占个楼，慢慢编辑……

#####

之所以拟合再次失败，是因为$x$是个变量$x(i)$，不是常量$x$。

只是$x(i)$这个变量变化得太慢了，以至于Fans只看到$x(i)$的一部分，就以为$x$是个常量。

第$1$次拟合，Fans看到的是$x(66)$，所以说$x=5/13$；

要真取了$x=5/13$吧？那结果就只是$a(66)$一致，其它不一致。

第$2$次拟合，Fans看到的是$x(1024)$，所以说$x=2/5$；

要真取了$x=2/5$吧？那结果就只是$a(1024)$一致，其它不一致。

想让$a(1048576)$一致？

得取$x=5/12$~

想让$a(2^31)$一致？

那$x$要取啥连Fans自己都不清楚，更别说其他网友了。

这题做到这，Fans已经精疲力尽了，需要休息一段时间，再回过头来搞$x(i)$这个鬼东西~

账号		自动登录	找回密码
密码			欢迎注册

[原创] KeyTo9无限升级的概率

评分

点评