Can You Solve The Probability Two Random Walkers Meet?

markfang2050

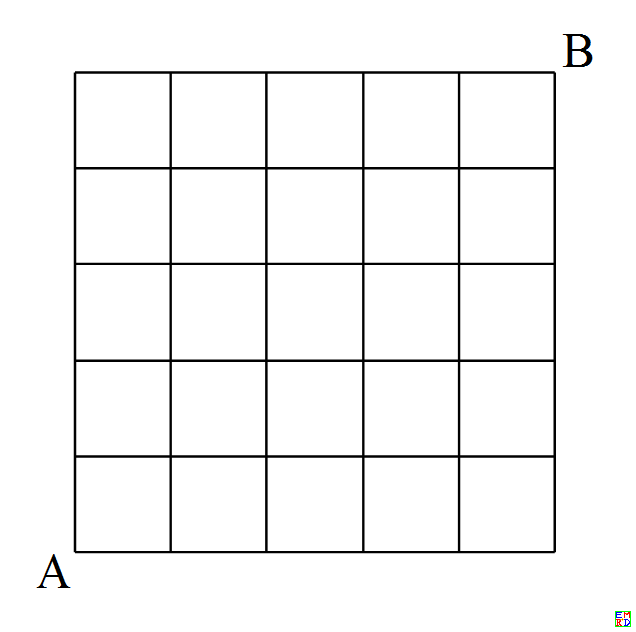
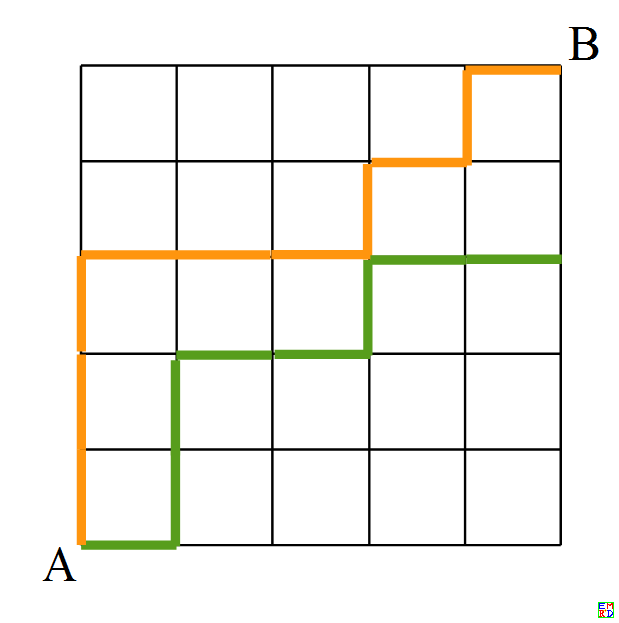
Points A and B are opposite corners of a 5×5 grid.
Alice starts at point A, and each second, walks one edge right or up (if a point has two options, each direction has a 50% chance) until Alice reaches point B.

At the same time, Bob starts at point B, and each second he walks one edge left or down (if a point has two options, each direction has a 50% chance) in order to reach point A.

What is the probability Alice and Bob meet during their random walks? (Meet means occupy the same point at the same time).

What is the probability for an n by n grid? What is the limiting probability as n goes to infinity?

计算机程序模拟与理论求解均可。
如果格子是5×9的呢？如何计算？
如果格子是m×n的呢？如何计算？（m,n是不相等的正整数，m>=2,n>=2.）

.·.·.

这不应该是显然的吗？
虽然上次说错了一次，但这次应该没错了
设A(0, 0), B(n, n), Alice与Bob相遇在(x, y)
在相遇时两人所走路程相同：x+y = (n-x)+(n-y) → x+y = n
即Alice跟Bob只能在反对角线 x+y= n 上相遇
到达反对角线上每一点的概率都是可以求的（极限是一个正态分布（？））
然后把所有求出来的结果合起来就好了
（显然n->无穷的时候这两个家伙永远不会相遇）

mathe

从A或B到达反对角线上各点的概率满足二项分布。
从A或B到达反对角线 x+y = n 上的点(x, y)的路径都是`C_n^x=\D\frac{n!}{x!y!}`条
选择每条路径的概率都是`1/2^n`
所以双方到达点(x, y)的概率都是`C_n^x/2^n`, 同时到达的概率则是该式的平方。
然后再求和，结果应该就是${C_{2n}^n}/{2^{2n}}~={sqrt(2\pi2n)({2n}/e)^{2n}}/{2\pi n (n/e)^{2n}2^{2n}} ~=O(1/{sqrt(\pi n)})$