- 注册时间
- 2023-3-12
- 最后登录
- 1970-1-1
- 威望
- 星
- 金币
- 枚
- 贡献
- 分
- 经验
- 点
- 鲜花
- 朵
- 魅力
- 点
- 上传
- 次
- 下载
- 次
- 积分
- 53
- 在线时间
- 小时
|
马上注册,结交更多好友,享用更多功能,让你轻松玩转社区。
您需要 登录 才可以下载或查看,没有账号?欢迎注册
×
介绍一个不需穷举试错的快速单偶数幻方构造法, 附关键部分js代码, 完整代码会在下一篇文章<将8x8幻方表示成两个2x8矩阵之有限域matmul的实验>中提供.
<正负>指的是有限域的"正负", 下文有解释.
若将(由一阶等差数组构成的)n阶幻方中每一元素表示成p*(n*a+b)+q, 当(p=1, q=1)时, 即常见的由1起始的连续整数幻方,
本文取(p=1, q=0), 即表示为由零起始至n^2-1的连续整数幻方.
简单地说, 即将幻方中每一元素表示成纯n*a+b, 不附带p与q的线性scale.
下一篇文章将称这种以ab表示幻方元素的方法为"二数字/二数位(2 digits)表示法".
已知, 当n为单偶数时, 能使n*n幻方M[y,x]中每一对(点对称的)元素, 即M[y,x]与M[n-1-y,n-1-x], 皆满足M[y,x]+M[n-1-y,n-1-x]=n^2-1之关系的排列法不存在.
至少需有两对(相加为n^2-1的)互补元素不是对中心点对称的. 例如以下6阶幻方, 幻和=105:
- 07 16 27 18 32 05
- 25 34 00 09 14 23
- 02 20 22 31 24 06
- 29 11 04 13 15 33
- 12 21 35 26 01 10
- 30 03 17 08 19 28
再以10阶为例, 以下幻方幻和=495:
- 00 25 89 39 96 71 42 92 08 33
- 50 75 64 14 21 46 17 67 58 83
- 72 97 18 43 80 55 79 04 36 11
- 22 47 68 93 05 30 29 54 86 61
- 59 34 01 51 62 87 73 23 90 15
- 84 09 76 26 12 37 48 98 65 40
- 38 13 45 70 94 69 06 31 52 77
- 88 63 95 20 44 19 56 81 02 27
- 16 41 32 82 53 78 85 35 24 49
- 66 91 07 57 28 03 60 10 74 99
我称这一类只有两对互补元素不对称的单偶数阶幻方为<最接近完全正负对称幻方>,
之所以称<正负>, 是因为在dim=n的有限域中, 若称一数u为"正数", 另一数v其与u的关系满足u+v=n^2-1, 则可称v为u的"负数"/变号数,
这种关系在二幂dim中显而易见, 例如在dim=8中, 假令数字3为"正数", 其二进制表示为b000011, 那么其"变号数"60的二进制表示就是b111100,
0与1恰好是反过来的, 3+60=8*8-1=63. 计算机中signed int的负数表示法与此类似.
又, 二维坐标M[y,x]若写成线性一维坐标, 即为M[y*n+x], 会编程的应该对此很熟悉,
如此前文所谓"对中心点对称"的二元素, 以一维坐标表示即M[y*n+x]与M[n^2-1-y*n-x], 这两个一维坐标相加对消后只剩下n^2-1, 与前述"正负数"相加为n^2-1共享同一规律.
现在我所谓<正负对称>的意义应该很明瞭了, 指的即是<既在数值上正负互补, 又在坐标上正负互补>,
以此故我将这种对称性视为一个幻方是否完美的重要指标, 在这个意义上我称这种<只有两对互补元素不对称的>单偶数阶幻方为<最接近完美的>.
-构造法(代码):
这种单偶数n的<最接近完美幻方>, 是由一个(n>>1)阶的奇幻方与一组通用LUXmap构成的,
就我在网上查幻方LUX构造法所知, 这种无需试错的LUXmap构造法应该尚未被人发现过.
首先是LUXmap的构造法, 这是本幻方构造法的关键所在:
- var cur_lx_size=0;
- const LUXele=[
- [0x1b,0x2d,0x6c],
- [0xe1,0xb1,0xe4]
- ];
- function buildlx(n)
- {
-
- if(n<=cur_lx_size){return;}
- LUXmap_width=n>>1;
- var qoddn=LUXmap_width>>1;
- LUXmap_height=qoddn+1;
- LUXmap = new Uint8Array(LUXmap_width*LUXmap_height);
- var staidx=qoddn-1;
- var lyn0=staidx*(LUXmap_width+1);
- LUXmap.set(LUXele[0], lyn0);
- lyn0+=LUXmap_width;
- LUXmap.set(LUXele[1], lyn0);
- if(staidx>0)
- {
- lyn0-=staidx;
- var toSouth=3+staidx;
- var wm1=LUXmap_width-1;
- var wp1=LUXmap_width+1;
- var gibidx=LUXmap_width+wm1;
-
- for(var d=0;d<staidx;d++)
- {
- LUXmap[d*LUXmap_width+qoddn]=0x9c; //west
- var fynlin=lyn0+d;
- LUXmap[fynlin]=0xe1; //north
- LUXmap[fynlin+toSouth]=0xb4; //south
- LUXmap[d*wp1]=0x1b; //NW
- LUXmap[(d+1)*wm1]=0x1b; //SW
- var fill_len=staidx-d;
- for(var kk=0;kk<fill_len;kk++)
- {
- var kk1d=kk+1+d;
- LUXmap[kk1d*LUXmap_width+d]=0xd8; //NW-n
- LUXmap[d*LUXmap_width+kk1d]=0xb1; //NW-w
- LUXmap[d*LUXmap_width+staidx+2+kk]=0x4e; //SW-w
- LUXmap[kk1d*LUXmap_width+wm1-d]=0x27; //SW-s
- }
- LUXmap[gibidx]=0x72;
- gibidx+=wm1;
- }
-
-
- }
- cur_lx_size=n;
- }
透过穷举得出, 乘16应该是包含了旋转/镜像/内外互换等; 因那两组不对称的"例外组"在第一行或第二行而分成两类, 故乘2,
至于基本"核"为何是3x19=57个, 希望有板友能给出数学证明.
代码中
- const LUXele=[
- [0x1b,0x2d,0x6c],
- [0xe1,0xb1,0xe4]
- ];
即是上述"核"中的一个, 其余一些可能的核有:
- -xl [0xc9,0x72,0xe1], [0x1b,0x4e,0x4b]
- -xl [0xc9,0x72,0xe1], [0x1e,0x4e,0x1b]
- xlx [0x27,0x2d,0x8d], [0xe1,0xb1,0xe4]
- xlx [0x27,0x2d,0x8d], [0xe4,0xb1,0xb4]
- xlx [0x72,0x78,0xd8], [0x4b,0x1b,0x4e]
- xlx [0x72,0x78,0xd8], [0x4e,0x1b,0x1e]
- -xx [0x93,0x8d,0xb1], [0x4b,0xb1,0x4e]
- ...等
选定了一个六阶核, 那么所有6+4N阶的LUXmap就能无须穷举试错地快速构造出来了, 即上述代码所做的事,
例如, 一个22阶的这种<最接近完美的>LUXmap看起来像这样:
- 0x1b,0xb1,0xb1,0xb1,0xb1, 0x9c, 0x4e,0x4e,0x4e,0x4e,0x1b,
- 0xd8, 0x1b,0xb1,0xb1,0xb1, 0x9c, 0x4e,0x4e,0x4e,0x1b, 0x72,
- 0xd8, 0xd8, 0x1b,0xb1,0xb1, 0x9c, 0x4e,0x4e,0x1b, 0x72, 0x27,
- 0xd8, 0xd8, 0xd8, 0x1b,0xb1, 0x9c, 0x4e,0x1b, 0x72, 0x27, 0x27,
- 0xd8, 0xd8, 0xd8, 0xd8, 0x1b,0x2d,0x6c, 0x72, 0x27, 0x27, 0x27,
- 0xe1, 0xe1, 0xe1, 0xe1, 0xe1,0xb1,0xe4, 0xb4, 0xb4, 0xb4, 0xb4]
其次是较不重要的实际幻方构造及LUXmap解码部分, 代码为:
- function mkmgsq_4Np2(n)
- {
- function fill_mir(y1,x1,zzsft)
- {
- var vlu=ady+ ((lxv>>zzsft)&3) *mulp;
- var ydx=(y0a+y1)*n+(x0a+x1);
- ret[ydx]=vlu;
- ret[lztm-ydx]=lztm-vlu;
- }
- function fill_nomir(y1,x1,zzsft) {ret[(y0a+y1)*n+(x0a+x1)]=ady+((lxv>>zzsft)&3)*mulp;}
- var oddhfn=n>>1;
- buildlx(n);
- var oddhf=odd_base_maker(oddhfn);
- var mulp=n*n;
- var lztm=mulp-1;
- var lztn=n-1;
- var ret = new Array(mulp);
- mulp>>=2;
- var oddhfhfn=(oddhfn>>1);
- var lxstp=LUXmap_height-oddhfhfn-1;
- for(var y=0;y<oddhfn;y++)
- {
- var y0a=y<<1;
- for(var x=0;x<oddhfhfn;x++)
- {
- var ady=oddhf[y*oddhfn+x];
- var x0a=x<<1;
- var lxv=LUXmap[(x+lxstp)*LUXmap_width+y+lxstp];
- fill_mir(0,0,6);
- fill_mir(0,1,4);
- fill_mir(1,0,2);
- fill_mir(1,1,0);
-
- }
- var ady=oddhf[y*oddhfn+x];
- var lxv=LUXmap[(oddhfhfn+lxstp)*LUXmap_width+y+lxstp];
- var x0a=oddhfhfn<<1;
- fill_nomir(0,0,6);
- fill_nomir(0,1,4);
- fill_nomir(1,0,2);
- fill_nomir(1,1,0);
-
- }
- return ret;
- }
- var siamcache={3:[7,0,5, 2,4,6, 3,8,1],5:[10, 9, 3, 22, 16,
- 17, 11, 5, 4, 23,
- 24, 18, 12, 6, 0,
- 1, 20, 19, 13, 7,
- 8, 2, 21, 15, 14]};
- function simplesiam(n)
- {
- return siamcache[n];
- }
- var odd_base_maker=simplesiam;
这种奇数dim的异或表(xor表, xor是有限域中不进位的"加法"), 有着挺漂亮的规律, 例如其右转45度后:
五阶:
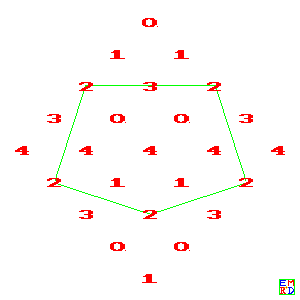
七阶:
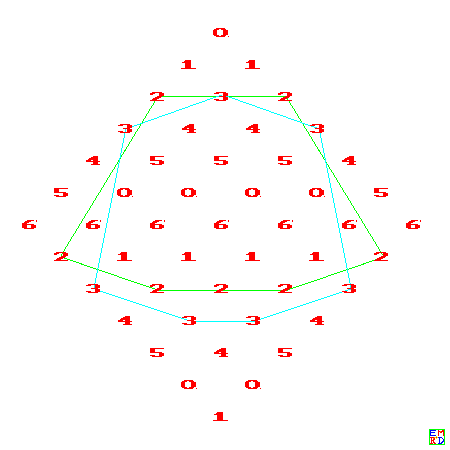
十一阶:

这也是就我所知还未被人发现过的.
|
|