- 注册时间
- 2016-5-4
- 最后登录
- 1970-1-1
- 威望
- 星
- 金币
- 枚
- 贡献
- 分
- 经验
- 点
- 鲜花
- 朵
- 魅力
- 点
- 上传
- 次
- 下载
- 次
- 积分
- 270
- 在线时间
- 小时
|
马上注册,结交更多好友,享用更多功能,让你轻松玩转社区。
您需要 登录 才可以下载或查看,没有账号?欢迎注册
×
数列a(n+1)=sqrt(S(n)^2-S(n)+2),其中S(n)是数列前n项和,求a(n)的表达式。
得到:a(n)=a3*sin(x)/sin(x/2^(n-3)) n>=3。
解:
如果a(1)=sqrt(2),可以构造三角形利用余弦定理,有:
a(n)=sqrt(14)/2/sin((pi-asin(sqrt(14)/4))/2^(n-1))。
这题对于任意a(1)都可以有解析表达式的。 可以写出连乘的出来。
先去掉S(n):
a(n+1)^2=S(n)^2-S(n)+2
a(n+2)^2=S(n+1)^2-S(n+1)+2
a(n+2)^2-a(n+1)^2=(S(n+1)+S(n))*a(n+1)-a(n+1)
=(2S(n+1)-a(n+1))*a(n+1)-a(n+1)
所以:
2S(n+1)=(a(n+2)^2+a(n+1))/a(n+1)
2S(n+2)=(a(n+3)^2+a(n+2))/a(n+2)
2a(n+2)=a(n+3)^2/a(n+2)-a(n+2)^2/a(n+1)
a(n+3)^2/a(n+2)^2=a(n+2)/a(n+1)+2
⚠️⚠️⚠️注意这个等式成立条件是n>=1
除了a1,a(n)都大于0。 可以验证一般情况下a(3)^2/a(2)^2 != a(2)/a(1)+2。
a(1)=sqrt(2)/4的时候,这个等式刚好成立。
设a(n+1)/a(n)=b(n),有:
b(n+1)^2=b(n)+2
b(n+1)=sqrt(2+b(n))
设b(1)=2*cosx
x=acos(b1/2)
cosx=2(cos(x/2))^2-1
所以:
b(n)=2cos(x/2^(n-1))
有:
a1=a1
a2=sqrt(a1*a1-a1+2)
a3=sqrt((a1+a2)^2-(a1+a2)+2)
b1=a(3)/a(2)
x=acos(b1/2)
a(n)=a2* 2^(n-2)*∏cos(x/2^(i-1)
(i取1到n-2) n>=3
a(n)=a3*sin(x)/sin(x/2^(n-3)) n>=3
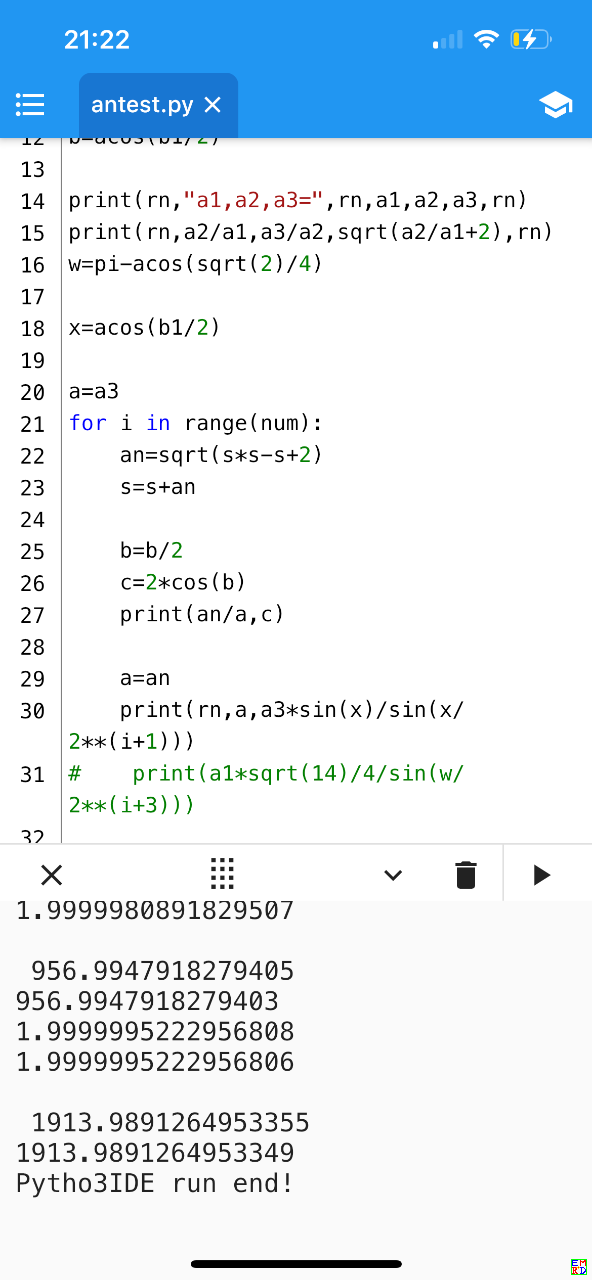
验证Python代码:
from math import *
rn="\r\n"
num=10
a1=sqrt(2)/2
s=a1
a2=sqrt(s*s-s+2)
s+=a2
a3=sqrt(s*s-s+2)
s+=a3
b1=a3/a2
b=acos(b1/2)
print(rn,"a1,a2,a3=",rn,a1,a2,a3,rn)
print(rn,a2/a1,a3/a2,sqrt(a2/a1+2),rn)
w=pi-acos(sqrt(2)/4)
x=acos(b1/2)
a=a3
for i in range(num):
an=sqrt(s*s-s+2)
s=s+an
b=b/2
c=2*cos(b)
print(an/a,c)
a=an
print(rn,a,a3*sin(x)/sin(x/2**(i+1)))
# print(a1*sqrt(14)/4/sin(w/2**(i+3)))
an是按递推公式计算得出来的,和an公式得到的吻合。a(n+1)/a(n)比值和公式b(n)比较,稳合。
|
-
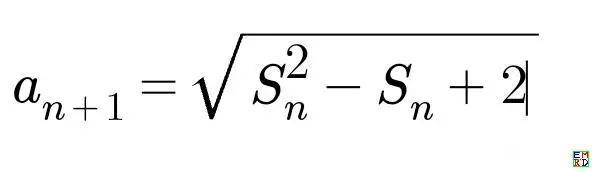
-
|