对于通用情况,计算估计比较困难,但是对于较小的n,用计算机计算还是可行的。
以4个球为例,我们可以把四球状态分为
4(4个球同色)
3+1(3个同色,1个不同色)
2+2(4个球两色,每色两球)
2+1+1
1+1+1+1
共5种不同状态
然后我们需要计算它们的状态转移矩阵
比如3+1状态,如果两个球都属于3,状态不变,概率1/2;第一个3,第二1,改为状态4,概率1/4;第一个1,第二个3,改为状态2+2,概率1/4.
最终我们可以得到如下状态转移图
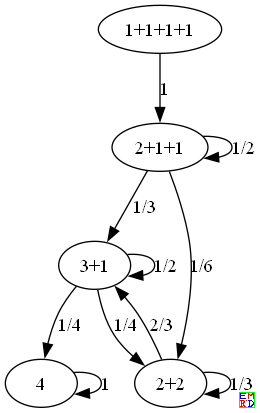
然后我们可以得出方程组
E(4)=0
E(3+1)=1+1/4*E(4)+1/2*E(3+1)+1/4*E(2+2)
E(2+2)=1+1/3*E(2+2)+2/3*E(3+1)
E(2+1+1)=1+1/2*E(2+1+1)+1/3*E(3+1)+1/6*E(2+2)
E(1+1+1+1)=1+E(2+1+1)
解得
E(1+1+1+1)=9,E(2+1+1)=8,E(2+2)=7,E(3+1)=11/2
所以平均需要9步。
同样可以得到5个球时
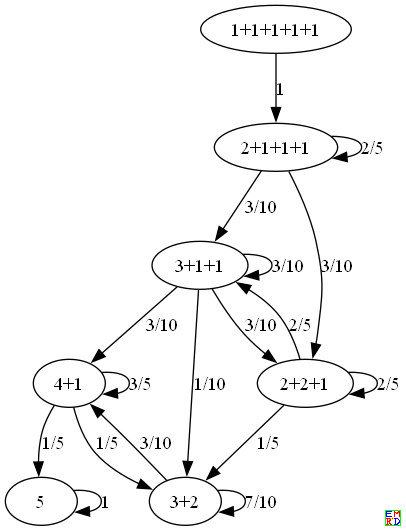
对应需要16步。
计算计算更多球的情况,可以得到如下结果
- (11:55) gp > (matid(4)-m)^-1*[1,1,1,1]~
- %11 = [9, 8, 11/2, 7]~
- (11:55) gp > ?ve
- vecextract vecmin vecsearch vecsum vectorsmall version
- vecmax vecprod vecsort vector vectorv
- (11:55) gp > m=[0,12,0,0;0,6,4,2;0,0,6,3;0,0,8,4];
- (11:58) gp > (matid(4)-m/12)^(-1)*[1,1,1,1]~
- %13 = [9, 8, 11/2, 7]~
- (11:58) gp > m=[0,20,0,0,0,0;0,8,6,6,0,0;0,0,6,6,6,2;0,0,8,8,0,4;0,0,0,0,12,4;0,0,0,0,6,14];
- (11:58) gp > (matid(6)-m/20)^(-1)*[1,1,1,1,1,1]~
- %15 = [16, 15, 38/3, 14, 25/3, 35/3]~
- <,0,24,6,0,0,0;0,0,0,0,0,0,0,20,5,0;0,0,0,0,0,0,0,8,14,8;0,0,0,0,0,0,0,0,18,12];
- (11:59) gp > (matid(10)-m/30)^(-1)*[1,1,1,1,1,1,1,1,1,1]~
- %17 = [25, 24, 87/4, 23, 107/6, 83/4, 22, 137/12, 101/6, 37/2]~
- <0,0,0,0,0,30,6,0;0,0,0,0,0,0,0,0,0,0,0,10,22,10;0,0,0,0,0,0,0,0,0,0,0,0,12,30];
- (12:00) gp > (matid(14)-m/42)^(-1)*[1,1,1,1,1,1,1,1,1,1,1,1,1,1]~
- %19 = [36, 35, 164/5, 34, 291/10, 159/5, 33, 117/5, 281/10, 148/5, 154/5, 147/10, 112/5, 259/10]~
- <,0,0,0,0,0,0,0,0,0,0,0,0,15,26,15;0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,32,24];
- (12:00) gp > (matid(21)-m/56)^(-1)*[1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1]~
- %21 = [49, 48, 275/6, 47, 634/15, 269/6, 46, 739/20, 619/15, 128/3, 263/6, 45, 293/10, 719/20, 391/10, 604/15, 125/3, 363/20, 283/10, 2027/60, 533/15]~
- <,0,0,0,0,18,36,18;0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,20,52];
- (12:01) gp > (matid(29)-m/72)^(-1)*[1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1]~
- %23 = [64, 63, 426/7, 62, 1205/21, 419/7, 61, 5492/105, 1184/21, 404/7, 412/7, 60, 1583/35, 5387/105, 1139/21, 1163/21, 397/7, 405/7, 1242/35, 1548/35, 5162/105, 5282/105, 1066/21, 1118/21, 382/7, 761/35, 1207/35, 1473/35, 1599/35]~
- <0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,50,40];
- <1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1]~
- %25 = [81, 80, 623/8, 79, 2085/28, 615/8, 78, 3895/56, 2057/28, 299/4, 607/8, 77, 4399/70, 3839/56, 3995/56, 2029/28, 295/4, 599/8, 76, 15087/280, 4329/70, 465/7, 3783/56, 951/14, 3939/56, 2001/28, 573/8, 291/4, 5869/140, 14807/280, 16721/280, 4259/70, 3529/56, 458/7, 937/14, 955/14, 7129/280, 5729/140, 3553/70, 7883/140, 1627/28]~
看来n个球平均需要$(n-1)^2$步 |