几何难题

leimou

Jack315

【证题思路】
如图所示：

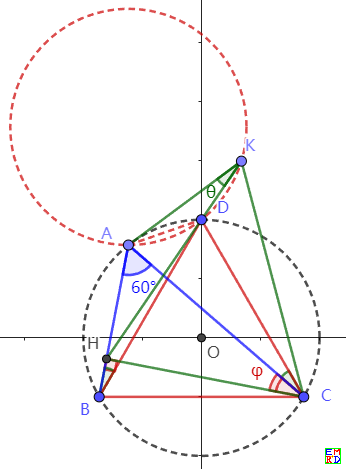
设正三角形 \(\triangle BCD\) 外接圆 \(P\) 的半径为 \(r\)，则 \(B,C,D\) 三点的坐标均为 \(r\) 的函数。
\(A,K\) 两点的坐标共四个变量。
\(\angle BAC=60\degree\) 表明 \(A\) 点在圆 \(P\) 上，得方程 1 。
由题中两个角度关系得方程 2 和 3 。
同时这两个角度关系说明 \(\theta=\angle AKD=\angle ABD=\angle ACD\) 。
这表明同一条弦 \(AD\) 对应的的两个角 \(\angle AKD\) 和 \(\angle ACD\) 相等，
即 \(\triangle AKD\) 的外接圆（红色）与圆 \(P\)（黑色）具有相同的半径，因而得方程 4 。
由这 4 个方程即可求出 \(A,K\) 两点的坐标（\(r\) 的函数）。
根据 \(A,B,C,D,K\) 五点的坐标，可求出 \(H\) 点的坐标（\(r\) 的函数）和 \(\varphi=\angle ACH\) 的正切值。
这个正切值应该与 \(r\) 无关，且为 \(\frac{1}{\sqrt{3}}\)，即 \(\varphi=30\degree\)，从而证得 \(CH\perp AB\) 。