作平行四边形的内切椭圆及椭圆的焦点

yigo

如图，已知平行四边形ABCD及AB边上一点E，求作与AB边切于点E的内切椭圆，并作出其焦点P1,P2。
过点E作对角线BD的平行线交AD边于H，点E，H旋转180度，分别得到BC边上的F点，CD边上的G点。
易知F,G,H是椭圆与另外三条边的切点。

yigo

若不限制E点，则平行四边形的内切椭圆的焦点轨迹是过A、B、C、D点的等轴双曲线，两个焦点P1，P2关于是四边形的中心O对称，如下图所示，
等轴双曲线的渐近线分别是过O点与∠A的角平分线平行、垂直的直线。以渐近线为坐标轴，则轨迹是反比例函数。
原题目等价于，已知直线l上的点E，直线l与反比例函数曲线交于A、B两点，在曲线上作点P1，P2（P2是P1关于O点的对称点），使得∠P1EA=∠P2EB。

yigo

看来下画法几何里面求椭圆主轴的脚本步骤，三百多步骤，看来就焦点也不容易。

yigo

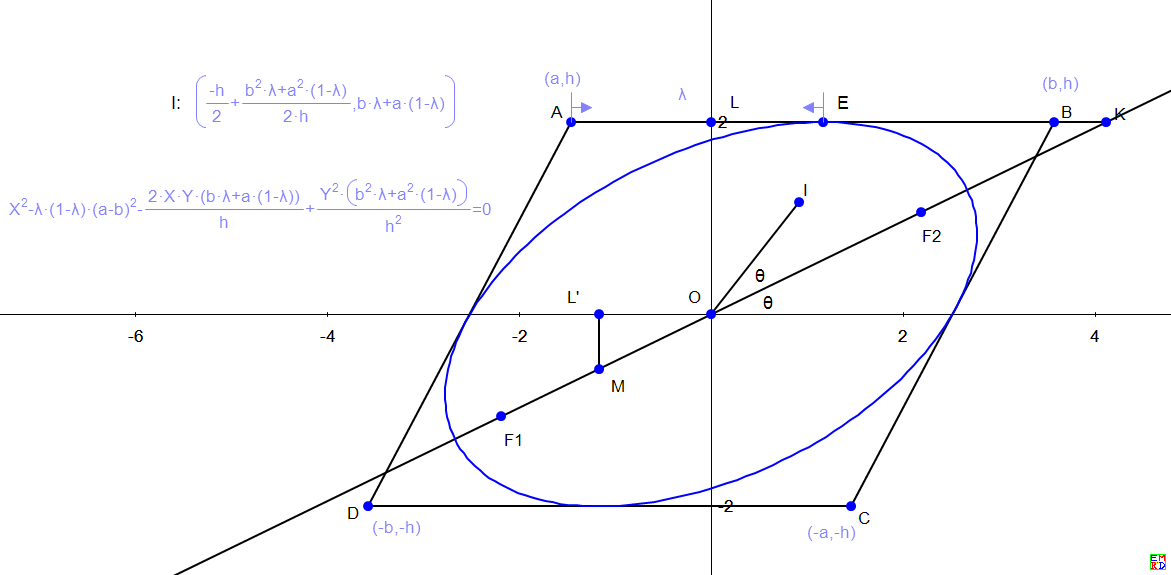
已经找到作图方法，总体思路分为两步：
1、确定椭圆主轴方向；
2、在主轴上找到焦点。
对于椭圆（或者双曲线）：\(px^2+qy^2-2rxy=1\)，其主轴与x轴的夹角\(\theta\)满足\(\tan2\theta=\frac{2r}{q-p}\)。
如下图建立坐标系，平行四边形各点的坐标如图中所示，\(\frac{EA}{AB}=\lambda\)，则：
\(p=\frac{1}{\lambda(1-\lambda)(b-a)^2}\)
\(q=\frac{(1-\lambda)a^2+\lambda b^2}{\lambda(1-\lambda)(b-a)^2h^2}\)
\(r=\frac{(1-\lambda)a+\lambda b}{\lambda(1-\lambda)(b-a)^2h}\)
\(\tan2\theta=\frac{2r}{q-p}=\frac{(1-\lambda)a+\lambda b}{(1-\lambda)\frac{a^2}{2h}+\lambda \frac{b^2}{2h}-\frac{h}{2}}\)
构造点\(I[(1-\lambda)\frac{a^2}{2h}+\lambda \frac{b^2}{2h}-\frac{h}{2},(1-\lambda)a+\lambda b)],OI\)与\(x\)轴的夹角为\(2\theta\)，
\((1-\lambda)a+\lambda b\)即是E点的横坐标，
在\(A\)点对应处给出坐标\((a,\frac{a^2}{2h}-\frac{h}{2})\)，在\(B\)点对应处给出坐标\((b,\frac{b^2}{2h}-\frac{h}{2})\)，
然后在\(E\)点对应处插值得到\([(1-\lambda)a+\lambda b,(1-\lambda)\frac{a^2}{2h}+\lambda \frac{b^2}{2h}-\frac{h}{2}]\)，然后以\(y=x\)轴镜像，就得到\(I\)点坐标。
作\(OI\)与x轴正向的角平分线，即为所求椭圆的主轴。

接下来就是在主轴上找到两焦点\(F_1,F_2\)，
由于\(E\)点是切点，所以\(∠F_1EA=∠F_2EB\),设\(OF_1=OF_2=c\),则：
\(c^2=\frac{OL}{\sin\theta}\frac{LE}{\cos\theta}=OM*OK\),焦点即已求出，
然后根据E点可求出椭圆长轴长度，椭圆即已作出。

如果只作椭圆，不要求焦点，则方法更简单，首先椭圆上的4个切点可以确定，只需要再找到椭圆上一点，就可以根据帕斯卡定理做出椭圆
根据方程易知，对角线\(OB\)与椭圆的交点\(B'\)满足\(OB'=\sqrt{\lambda}OB\),对角线\(OA\)与椭圆的交点\(A'\)满足\(OA'=\sqrt{1-\lambda}OA\)。

hejoseph

利用切点位置可以把平行四边形的内切椭圆仿射为菱形的内切圆获得椭圆的第五点，然后可以用五点作图法得到主轴焦点位置，椭圆的一组共轭直径就是平行四边形的对角线。
https://bbs.emath.ac.cn/forum.ph ... 16093&pid=78811
上面的链接有作图方法。
当然对于平行四边形的特殊情形应该有比较简单的方法。

hejoseph

设平行四边形 \(ABCD\) 对角线 \(AC\)、\(BD\) 相交于点 \(O\)，内切椭圆分别与 \(DA\)、\(AB\)、\(BC\)、\(CD\) 相切于点 \(S\)、\(T\)、\(U\)、\(V\)，\(AC=2e\)，\(BD=2f\)，\(AC\) 与 \(BD\) 的夹角为 \(\theta\)，\(AS:SD=w_1:w_2\)，\(w_1+w_2=1\)，内切椭圆长半轴长为 \(a\)，短半轴长为 \(b\)，长轴与 \(AC\)、\(BD\) 的夹角分别为 \(\theta_1\)、\(\theta_2\)，则长轴一定位于 \(AC\)、\(BD\) 所夹锐角的那部分之内，
\begin{align*}
OA_1&=e\sqrt{w_2}\\
OB_1&=f\sqrt{w_1}\\
a&=\sqrt{\frac{e^2w_2+f^2w_1+\sqrt{e^4w_2^2+f^4w_1^2+2e^2f^2w_1w_2\cos 2\theta}}{2}}\\
b&=\sqrt{\frac{e^2w_2+f^2w_1-\sqrt{e^4w_2^2+f^4w_1^2+2e^2f^2w_1w_2\cos 2\theta}}{2}}\\
\tan\theta_1&=\frac{\sqrt{e^4w_2^2+f^4w_1^2+2e^2f^2w_1w_2\cos 2\theta}-e^2w_2-f^2w_1\cos 2\theta}{f^2w_1\sin 2\theta}\\
\tan\theta_2&=\frac{\sqrt{e^4w_2^2+f^4w_1^2+2e^2f^2w_1w_2\cos 2\theta}-e^2w_2\cos 2\theta-f^2w_1}{e^2w_2\sin 2\theta}
\end{align*}

yigo

hejoseph 发表于 2025-4-11 09:39
利用切点位置可以把平行四边形的内切椭圆仿射为菱形的内切圆获得椭圆的第五点，然后可以用五点作图法得到主 ...

看了最后一楼，给定5点，以其中三点构成的三角形，另外两点做这个三角形的等角共轭点，两个共轭点的连线就是5点圆锥曲线关于这个三角形的等角共轭像，用这种方法可以作出曲线，还可以知道曲线的离心率。
好奇这个离心率公式怎么证明。

hejoseph

摘取一些片段，可以完成这个题目的作图