四边形 n 等分网格之中心格的面积

hujunhua

如图，将一个四边形对边 的各n（正奇数）等分点顺序连线，求证中心的小四边形面积为原大四边形面积的1/n^2.

hujunhua

这个应该算不得难题，所以没有发在难题征解版块。解决方法很多，下面是一种纯代数解法（以n=5为例），用向量表示封装（打开封装的话，看到的公式就没这么简明了）。 解法基于两个事实： 1、直线AB上的点可以写成aA+bB, 这里a,b为实数，a+b=1。反过来也成立，这是一一对应的。 比如，AB上的从A到B的第m个n等分点的向量为${n-m}/nA+m/nB$ 2、凸四边形ABCD（逆时针方向）的面积记为S，则2S=A×B+B×C+C×D+D×A=(A-C)×(B-D). 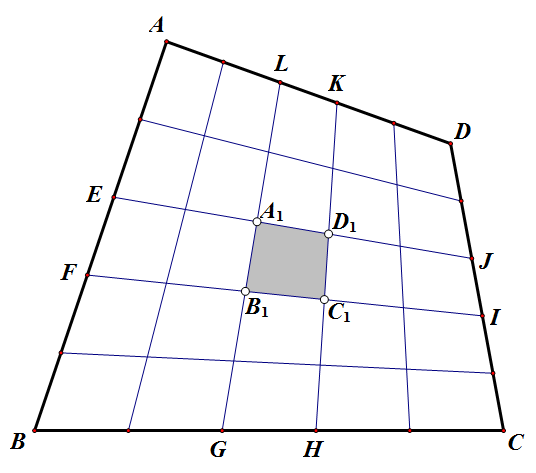如图，四边形ABCD的中心格由第(n-1)/2条和(n+1)/2条经线和纬线围成。为简化输入，就以n=5为例。。 第(n-1)/2条纬线EJ端点为E=0.6A+0.4B, J=0.4C+0.6D 第(n-1)/2条经线GL端点为G=0.6B+0.4C, L=0.6A+0.4D 我们猜测中心格的各顶点A', B', C', D' 也是所在经、纬线的 n 等分点，这个容易验证 纬线EJ的第2个5等分点为0.6E+0.4J=0.36A+0.24B+0.16C+0.24D 经线GL的第3个5等分点为0.4G+0.6L=0.36A+0.24B+0.16C+0.24D 这是同一点，所以就是EJ与GL的交点A'. 同理，B'=0.24A+0.36B+0.24C+0.16D, C'=0.16A+0.24B+0.36C+0.24D, D'=0.24A+0.16B+0.24C+0.36D 中心格A'B'C'D'的面积记为S'，那么2S'=(A'-C')×(B'-D')=0.2(A-C)×0.2(B-D)=0.04(2S), 即S'=S/25. 对于一般情况，将0.6换成(n+1)/2n, 0.4换成(n-1)/2n即可, 相应的，0.36、0.24、0.16分别换成${(n+1)^2}/{4n^2}, {n^2-1}/{4n^2},{(n-1)^2}/{4n^2}$。

wayne

看到这张帆布，我有一种冲动， 狠想 从A点出发，滑到0.1G+0.9H 点