椭圆上相距定长两点的切线交点的轨迹？

葡萄糖

椭圆上相距定长两点的切线交点的轨迹？

葡萄糖

数学星空

设椭圆方程为\(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\),则有椭圆上相距L两点的切线交点轨迹为：

\[(a^2y^2+b^2x^2)^2L^2+4(a^2b^2-a^2y^2-b^2x^2)(a^4y^2+b^4x^2)=0\]

上面结果由下列方程消元得到

\(\frac{y-y_1}{x-x_1}+\frac{b^2x_1}{a^2y_1}=0\)

\(\frac{y-y_2}{x-x_2}+\frac{b^2x_1}{a^2y_2}=0\)

\((x_1-x_2)^2+(y_1-y_2)^2-L^2=0\)

\(\frac{x_1^2}{a^2}+\frac{y_1^2}{b^2}=1\)

\(\frac{x_2^2}{a^2}+\frac{y_2^2}{b^2}=1\)

代入
\(x_1 =\frac{ a(-t^2+1)}{t^2+1}\)

\(y_1 =\frac{2bt}{t^2+1}\)

\(x_2 =\frac{ a(-s^2+1)}{s^2+1}\)

\(y_2 =\frac{2bs}{s^2+1}\)

得到

\(abs^2+bs^2x-2asy+ab-bx＝0\)

\(abt^2+bt^2x-2aty+ab-bx＝0\)

\(-L^2s^4t^4-2L^2s^4t^2-2L^2s^2t^4+4b^2s^4t^2-8b^2s^3t^3+4b^2s^2t^4-L^2s^4-4L^2s^2t^2-L^2t^4+4a^2s^4-8a^2s^2t^2+4a^2t^4-8b^2s^3t+16b^2s^2t^2-8b^2st^3-2L^2s^2-2L^2t^2+4b^2s^2-8b^2st+4b^2t^2-L^2＝0\)

然后消元s,t即可得到上面结果


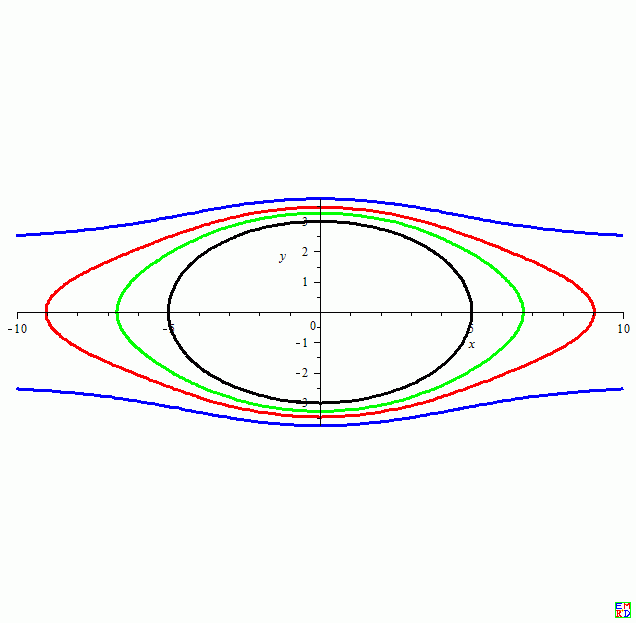
取\(a=5,b=3\),依次取\(L=4,5,6\)得到下面图形（绿，红，蓝，黑色为原椭圆）