动椭圆的运动区域的面积

葡萄糖

一个给定大小的恒过两点的动椭圆的运动区域的面积

数学星空

这个问题计算量很大：

可以设椭圆的一般方程为

\[\frac{\Big((x-s)\sin(\theta)+(y-t)\cos(\theta)\Big)^2}{m^2}+\frac{\Big(-(x-s)\cos(\theta)+(y-t)\sin(\theta)\Big)^2}{n^2}=1\]

由于椭圆过定点\((x_1,y_1),(x_2,y_2)\)代入方程

\[\left\{ \begin{split}\frac{\Big((x_1-s)\sin(\theta)+(y_1-t)\cos(\theta)\Big)^2}{m^2}+\frac{\Big(-(x_1-s)\cos(\theta)+(y_1-t)\sin(\theta)\Big)^2}{n^2}&=1\\
\frac{\Big((x_2-s)\sin(\theta)+(y_2-t)\cos(\theta)\Big)^2}{m^2}+\frac{\Big(-(x_2-s)\cos(\theta)+(y_2-t)\sin(\theta)\Big)^2}{n^2}&=1\end{split} \right.\]

然后作代换\(\sin(\theta)=\dfrac{2r}{1+r^2},\cos(\theta)=\dfrac{1-r^2}{1+r^2}\)

消元\({s,t}\),再对\(r\)求导，再消元\(r\)即可得到椭圆扫过的边界方程

例如取\(m=5,n=3,x_1=1,y_1=1,x_2=-1,y_2=-1\)容易算得

\(10625r^{12}x^4+7650r^{12}x^2y^2+1377r^{12}y^4+20000r^{11}x^4+54400r^{11}x^3y+14400r^{11}x^2y^2+19584r^{11}xy^3+2592r^{11}y^4-114850r^{12}x^2+171900r^{12}xy-96354r^{12}y^2+9350r^{10}x^4+102400r^{10}x^3y+150348r^{10}x^2y^2+36864r^{10}xy^3+27846r^{10}y^4-80000r^{11}x^2-131584r^{11}xy-10368r^{11}y^2-42400r^9x^4+23936r^9x^3y+239808r^9x^2y^2+198016r^9xy^3+44640r^9y^4+19652r^{12}-717516r^{10}x^2+752872r^{10}xy-688972r^{10}y^2+11407r^8x^4-262144r^8x^3y+114750r^8x^2y^2+262144r^8xy^3+168623r^8y^4+110976r^{11}+38528r^9x^2-656896r^9xy-309632r^9y^2+68672r^7x^4-30464r^7x^3y-561024r^7x^2y^2+178432r^7xy^3+173120r^7y^4+326808r^{10}-1164670r^8x^2+2578500r^8xy-2003390r^8y^2+25364r^6x^4+319488r^6x^3y-55896r^6x^2y^2-598016r^6xy^3+284308r^6y^4+464000r^9+118528r^7x^2+523264r^7xy-299264r^7y^2-68672r^5x^4+30464r^5x^3y+561024r^5x^2y^2-178432r^5xy^3-173120r^5y^4+294780r^8-2172584r^6x^2+3995056r^6xy-1772968r^6y^2+11407r^4x^4-262144r^4x^3y+114750r^4x^2y^2+262144r^4xy^3+168623r^4y^4-171264r^7-118528r^5x^2-523264r^5xy+299264r^5y^2+42400r^3x^4-23936r^3x^3y-239808r^3x^2y^2-198016r^3xy^3-44640r^3y^4-24752r^6-1164670r^4x^2+2578500r^4xy-2003390r^4y^2+9350r^2x^4+102400r^2x^3y+150348r^2x^2y^2+36864r^2xy^3+27846r^2y^4+171264r^5-38528r^3x^2+656896r^3xy+309632r^3y^2-20000rx^4-54400rx^3y-14400rx^2y^2-19584rxy^3-2592ry^4+294780r^4-717516r^2x^2+752872r^2xy-688972r^2y^2+10625x^4+7650x^2y^2+1377y^4-464000r^3+80000rx^2+131584rxy+10368ry^2+326808r^2-114850x^2+171900xy-96354y^2-110976r+19652＝0\)

然后对\(r\)求导并消元，其实表达式也惊人的长

我们可以画出轨迹图如下：

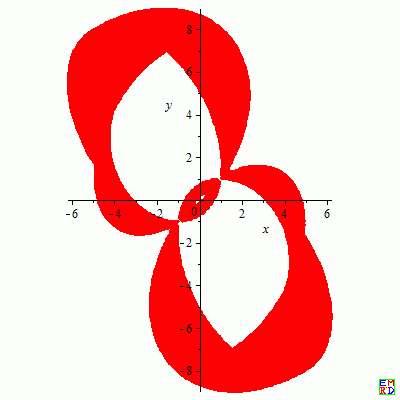
hujunhua

从2#的图上看，星空有增解需要舍弃。

如果椭圆只是靠着两定点滑动，扫掠区域只有上面所画的一半（如下图所示）。

星空将扫掠区域的镜像（以两定点连线为镜像线）混进去了。
扫掠区域是关于两定点连线的中垂线轴对称的，星空描绘的区域不全。

数学星空

wayne

给定大小是什么意思

数学星空

对于椭圆中心在x轴上的运动轨迹问题：

可以设椭圆的方程为

\[\frac{\Big((x-x_0)\sin(t)+(y-a)\cos(t)\Big)^2}{a^2}+\frac{\Big(-(x-x_0)\cos(t)+(y-a)\sin(t)\Big)^2}{b^2}=1\]

且 \[x_0=a {\Large\int}_0^t{\sqrt{1-\frac{a^2-b^2}{a^2}\sin(\theta)^2}\dif\theta}\]

则包络曲线就是对\(t\)求导后，消元\(t\)后的表达式（不能用初等函数表达）

例如：取\(a=5,b=3\),我们可以得到如下轨迹图

数学星空

对于椭圆在x轴上的运动轨迹问题：

可以设椭圆的方程为

\[\frac{\Big((x-x_0)\cos(t)+(y-y_0-b)\sin(t)\Big)^2}{a^2}+\frac{\Big(-(x-x_0)\sin(t)+(y-y_0-b)\cos(t)\Big)^2}{b^2}=1\]

且 \[x_0=a {\Large\int}_0^t{\sqrt{1-\frac{a^2-b^2}{a^2}\sin(\theta)^2}\dif\theta}\]

当 \(x=x_0,y=0\) 时，\(y'=0\)

则包络曲线就是对\(t\)求导后，消元\(t\)后的表达式（不能用初等函数表达）

例如：取\(a=5,\ b=3\),我们可以得到如下轨迹图

creasson

葡萄糖

给个动态图！