- 注册时间
- 2009-5-22
- 最后登录
- 1970-1-1
- 威望
- 星
- 金币
- 枚
- 贡献
- 分
- 经验
- 点
- 鲜花
- 朵
- 魅力
- 点
- 上传
- 次
- 下载
- 次
- 积分
- 38780
- 在线时间
- 小时
|
楼主 |
发表于 2016-10-12 09:40:04
|
显示全部楼层
我们首先把手牌的范围扩大:
——————————
手牌一共有$n$种。
下注和比牌规则不变。
——————————
接下来讨论策略。
策略:状态 → 行动
对于先手来说,每种手牌就是一种状态,一共有$n$种状态。
每种状态有$4$种行动:弃、跟弃、跟跟、加。
弃:弃牌
跟弃:跟注,被加注就弃牌
跟跟:跟注,被加注就跟注
加:加注
所以一共有$4\times 4\times 4\times\cdots\times 4=4^n$种策略。
对于后手来说,状态 = 手牌 × 局面,
手牌有$n$种,局面有$2$种:被跟注、被加注,
所以一共有$2n$种状态。
每种状态都有$2$种行动:
被跟注:看牌、加注
被加注:弃牌、跟注
所以一共有$2\times 2\times 2\times\cdots\times 2=2^{2n}=4^n$种策略。
接下来就可以列出一张$4^n\times 4^n$的盈亏表了,
表的每一行表示我方的一个策略,每一列表示对方的一个策略,
每个单元格是我方策略与对方策略对战后的我方收益。
当$n=2$时,手工打表足矣,参见楼上。
当$n>2$时,手工打表就很吃力了,得编程打表。
程序正在编写,请大家静候佳音。
#####
程序编写完成。
运行$n=3$,得到一个$64\times 64$的收益矩阵。
通过分析收益矩阵,得到我方的最佳策略只有$1$种:
小 → 弃牌;中 → 加注;大 → 加注。
对方的最佳策略也只有$1$种:
小 → 看牌/弃牌;中 → 加注/跟注;大 → 加注/跟注。
#####
运行$n=4$,得到一个$256\times 256$的收益矩阵。
通过分析收益矩阵,发现双方所有的固定打法都不是最佳策略。
为什么会出现这样的结果呢?
我们举一个简单的例子:
——————————
在剪刀石头布游戏里,有$3$种固定的策略:
$1$、把把出剪刀
$2$、把把出石头
$3$、把把出布
但这$3$种固定的策略都不是最佳策略。
该游戏的最佳策略是以$1/3$的概率出剪刀、以$1/3$的概率出石头、以$1/3$的概率出布。
如果不同的赢法得分不一样,出剪刀、石头、布的概率还得相应地调整,以获得尽可能高的期望得分。
参见 mathe 大师在 http://bbs.emath.ac.cn/thread-3645-1-1.html 作出的解答。
——————————
当$n=4$时,
我方的最佳策略是把以下$4$种固定的策略按照特定的概率($p_1$、$p_2$、$p_3$、$p_4$)随机选取一种。
$1$、最大 → 加注;次大 → 跟跟;次小 → 弃牌;最小 → 弃牌。
$2$、最大 → 加注;次大 → 跟跟;次小 → 跟弃;最小 → 弃牌。
$3$、最大 → 加注;次大 → 跟跟;次小 → 加注;最小 → 弃牌。
$4$、最大 → 加注;次大 → 跟跟;次小 → 加注;最小 → 加注。
选取概率必需满足这些条件:$p_2=0.5$,$p_1+p_3+p_4=0.5$,$p_1\leq 2p_4+p_3/2$,$p_4\leq p_1+p_3/2$。
以$p_1=p_4=0,p_2=p_3=0.5$为例,以上$4$种策略就组合成这样的最佳策略了:
最大 → 加注;次大 → 跟跟;次小 → 抛硬币,正面加注,反面跟弃;最小 → 弃牌。
对方的最佳策略是把以下$4$种固定的策略按照特定的概率($q_1$、$q_2$、$q_3$、$q_4$)随机选取一种。
$1$、最大 → 加注/跟注;次大 → 看牌/跟注;次小 → 看牌/弃牌;最小 → 看牌/弃牌。
$2$、最大 → 加注/跟注;次大 → 看牌/跟注;次小 → 看牌/弃牌;最小 → 加注/弃牌。
$3$、最大 → 加注/跟注;次大 → 加注/跟注;次小 → 看牌/弃牌;最小 → 看牌/弃牌。
$4$、最大 → 加注/跟注;次大 → 加注/跟注;次小 → 看牌/弃牌;最小 → 加注/弃牌。
选取概率必需满足这些条件:$q_1+q_2+q_3+q_4=1$,$q_1=q_4$,$q_2=q_3$。
以$q_1=q_2=q_3=q_4=0.25$为例,以上$4$种策略就组合成这样的最佳策略了:
最大 → 加注/跟注;次大 → 抛硬币,正面 加注/跟注,反面 看牌/跟注;次小 → 看牌/弃牌;最小 → 抛硬币,正面 加注/弃牌,反面 看牌/弃牌。
#####
运行$n=5$,得到一个$1024\times 1024$的收益矩阵。
通过分析收益矩阵,得到我方的最佳策略:
最大 → $3/4$加注,$1/4$跟跟;次大 → 跟跟;中 → $1/4$跟跟,$3/4$跟弃;次小 → $1/4$加注,$3/4$弃牌;最小 → 弃牌。
对方的最佳策略:
最大 → 加注/跟注;次大 → ($7/8$加注,$1/8$看牌)/跟注;中 → 看牌/($1/2$弃牌,$1/2$跟注);次小 → ($5/8$加注,$3/8$看牌)/弃牌;最小 → 看牌/弃牌。
#####
运行$n=6$,得到一个$4096\times 4096$的收益矩阵。
通过分析收益矩阵,得到我方的最佳策略:
最大 → $3/4$加注,$1/4$跟跟;次大 → 加注;中上 → 跟跟;中下 → $1/4$跟跟,$3/4$跟弃;次小 → $7/12$加注,$5/12$弃牌;最小 → 弃牌。
对方的最佳策略:
最大 → 加注/跟注;次大 → 加注/跟注;中上 → ($1/4$加注,$3/4$看牌)/跟注;中下 → 看牌/弃牌;次小 → ($3/4$加注,$1/4$看牌)/弃牌;最小 → 看牌/弃牌。
#####
运行$n=7$,得到一个$16384\times 16384$的收益矩阵。
通过分析收益矩阵,得到我方的最佳策略:
最大 → $3/4$加注,$1/4$跟跟;次大 → 加注;中上 → 跟跟;中中 → $1/4$跟跟,$3/4$跟弃;中下 → $7/12$加注,$5/12$弃牌;次小、最小 → 弃牌;
对方的最佳策略:
最大、次大 → 加注/跟注;中上 → ($5/8$加注,$3/8$看牌)/跟注;中中 → 看牌/($1/2$弃牌,$1/2$跟注);中下 → 看牌/弃牌;次小 → ($7/8$加注,$1/8$看牌)/弃牌;最小 → 看牌/弃牌。
#####
根据上述结果依次类推,得到$n=8$时,我方的最佳策略:
最大 → $3/4$加注,$1/4$跟跟;次大、第三 → 加注;第四 → 跟跟;倒四 → $1/4$跟跟,$3/4$跟弃;倒三 → $11/12$加注,$1/12$弃牌;次小、最小 → 弃牌。
对方的最佳策略:
前三 → 加注/跟注;第四 → 看牌/跟注;倒四 → 看牌/弃牌;倒三 → 加注/弃牌;次小、最小 → 看牌/弃牌。
#####
根据上述结果依次类推,得到$n=+\infty$时,我方的最佳策略:
前$1/4$ → 加注;$1/4$ 到 正中间 → 跟跟;正中间 到 倒数$3/8$ → 跟弃;倒数$3/8$ 到 倒数$7/24$ → 加注;后$7/24$ → 弃牌。
对方的最佳策略:
被加注时:前$1/2$ → 跟注;后$1/2$ → 弃牌;
被跟注时:前$3/8$ → 加注;$3/8$ 到 倒数$3/8$ → 看牌;倒数$3/8$ 到 倒数$1/4$ → 加注;后$1/4$ → 看牌。
如下图所示:
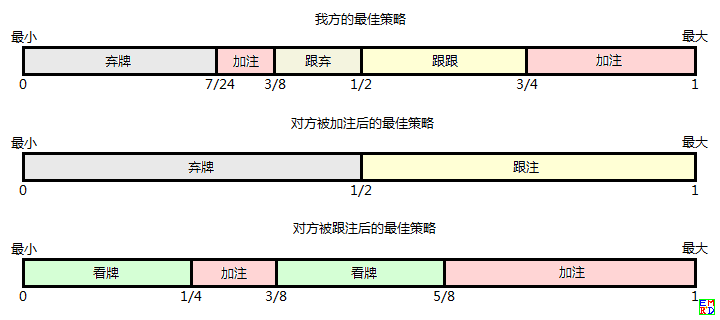
从上图可以看出,单手牌单轮下注的最基本打法是拿到大牌就加注、跟注,拿到小牌就看牌、弃牌。
但是加注行为都由$2$条线段组成:
拿大牌加注是想引诱对方跟注来获利,称为价值下注(value bet);
拿小牌加注是想逼迫对方弃牌来获利,称为诈唬(bluff)。
诈唬的比例必需恰到好处(在上述规则下,双方皆为$1/4$),
这样加注可以使得被加注的一方由于不知道对方是大牌还是小牌,
拿到中间牌的时候就进退两难了:跟也不是(损失筹码的期望值恰好是$2$),弃也不是(必定损失$2$筹码),
于是加注方的利益得到了最大化。
而诈唬的比例稍高一点、稍低一点都不是最佳策略,都会被对方利用。
我们接下来将下注额的范围扩大,看看该怎么打。 |
|