数学研发网设为首页收藏本站
切换到窄版

 找回密码
 欢迎注册
数学研发论坛»论坛 › 【数学研究】 › 数学软件 › mathematica 机器证明平面几何定理【例 2】 ...
返回列表 发新帖
查看: 28437|回复: 8

[分享] mathematica 机器证明平面几何定理【例 2】

[复制链接]
TSC999
发表于 2017-5-24 09:44:47 | 显示全部楼层 |阅读模式

马上注册，结交更多好友，享用更多功能，让你轻松玩转社区。

您需要 登录 才可以下载或查看，没有账号？欢迎注册

×
任意画一个不等边的五角星，图中有五个三角形，它们的外接圆交于 10 个点，其中新产生的有5个。证明新产生的五个交点 A2, B2, C2, D2, E2共圆，如图：

五点共圆图.png

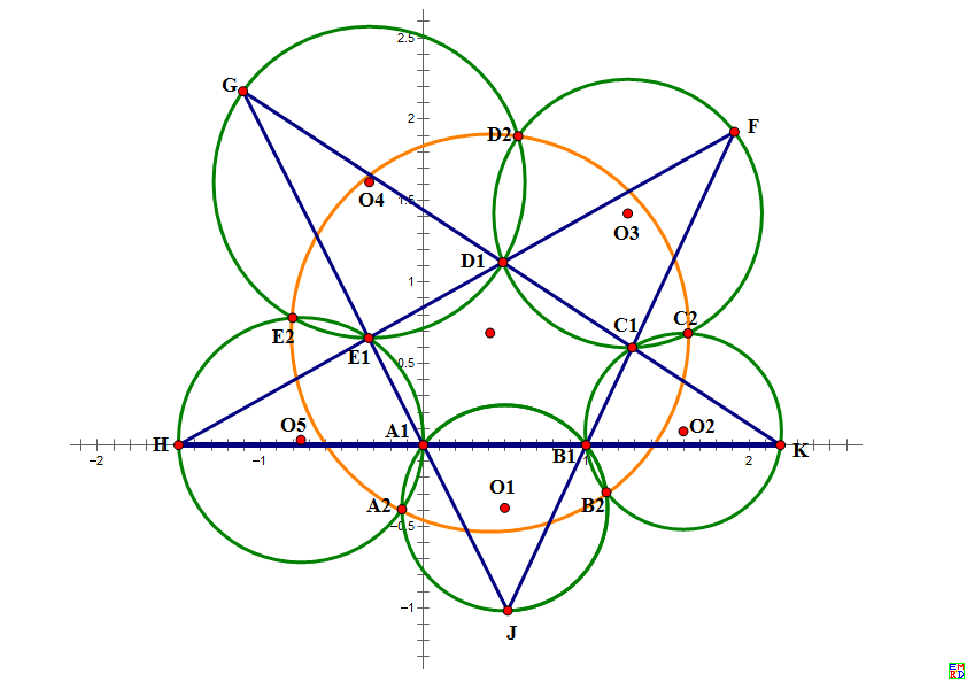
机器证明的程序如下：
  1. Clear[a, b, u, v, s, t] ;      
  2. a1 = 0 + 0  I;
  3. b1 = 1 + 0  I;
  4. c1 = a + b  I;   
  5. d1 = u + v  I;
  6. e1 = s + t  I;  
  7. Simplify[{0, "\!\(\*
  8. StyleBox["五个圆的内侧交点坐标",\nFontSize->10,\nFontColor->RGBColor[1, 0, 0]\
  9. ]\)", a1, b1, c1, d1, e1}]
  10. Jd[a_, b_, c_,
  11.   d_] := ((c - d) (b Conjugate[a] - a Conjugate[b]) - (a -
  12.      b) (d Conjugate[c] - c Conjugate[d]))/((c - d) (Conjugate[a] -
  13.      Conjugate[b]) - (a - b) (Conjugate[c] - Conjugate[
  14.      d])); (* 直线 AB 与 CD 的交点坐标 *)
  15. f = FunctionExpand[Jd[b1, c1, d1, e1],
  16.   Element[{a, b, u, v, s, t}, Reals]]; (*直线 B1C1 与 D1E1 的交点坐标*)
  17. g = FunctionExpand[Jd[c1, d1, a1, e1],
  18.   Element[{a, b, u, v, s, t}, Reals]];
  19. h = FunctionExpand[Jd[a1, b1, d1, e1],
  20.    Element[{a, b, u, v, s, t}, Reals]];
  21. j = FunctionExpand[Jd[b1, c1, a1, e1],
  22.    Element[{a, b, u, v, s, t}, Reals]];
  23. k = FunctionExpand[Jd[a1, b1, c1, d1],
  24.    Element[{a, b, u, v, s, t}, Reals]];
  25. Simplify[{1, "\!\(\*
  26. StyleBox["五角星的五个顶点坐标",\nFontSize->10,\nFontColor->RGBColor[1, 0, 0]\
  27. ]\)", f, g, h, j, k}]

  29. Wx[a_, b_, c_] := (
  30. a (c - b) a\[Conjugate] + b (a - c) b\[Conjugate] +
  31.   c (b - a) c\[Conjugate])/((c - b) a\[Conjugate] + (a -
  32.      c) b\[Conjugate] + (b -
  33.      a) c\[Conjugate]);   (* 三角形 ABC 的外心坐标 *)
  34. o1 = FunctionExpand[Wx[a1, b1, j],
  35.   Element[{a, b, u, v, s, t},
  36.    Reals]]; (* \[EmptyUpTriangle]A1B1J 的外心坐标 *)
  37. o2 = FunctionExpand[Wx[b1, c1, k], Element[{a, b, u, v, s, t}, Reals]];
  38. o3 = FunctionExpand[Wx[c1, d1, f], Element[{a, b, u, v, s, t}, Reals]];
  39. o4 = FunctionExpand[Wx[d1, e1, g], Element[{a, b, u, v, s, t}, Reals]];
  40. o5 = FunctionExpand[Wx[a1, e1, h], Element[{a, b, u, v, s, t}, Reals]];
  41. Simplify[{2, "\!\(\*
  42. StyleBox["五个三角形的外心坐标",\nFontSize->10,\nFontColor->RGBColor[1, 0, 0]\
  43. ]\)", o1, o2, o3, o4, o5}]

  45. Dchd[p_, a_, b_] := (
  46. b a\[Conjugate] - b\[Conjugate] a + (a - b) p\[Conjugate])/(
  47. a\[Conjugate] - b\[Conjugate]);  (* p 点关于直线 XY 的镜像点 *)
  48. a2 = FunctionExpand[Dchd[a1, o5, o1],
  49.   Element[{a, b, u, v, s, t}, Reals]]; (* A1点关于直线 O5O1 的镜像点 *)
  50. b2 = FunctionExpand[Dchd[b1, o1, o2],
  51.   Element[{a, b, u, v, s, t}, Reals]];
  52. c2 = FunctionExpand[Dchd[c1, o2, o3],
  53.    Element[{a, b, u, v, s, t}, Reals]];
  54. d2 = FunctionExpand[Dchd[d1, o3, o4],
  55.    Element[{a, b, u, v, s, t}, Reals]];
  56. e2 = FunctionExpand[Dchd[e1, o4, o5],
  57.    Element[{a, b, u, v, s, t}, Reals]];
  58. Simplify[{3, "\!\(\*
  59. StyleBox["五个圆的外侧交点坐标",\nFontSize->10,\nFontColor->RGBColor[1, 0, 0]\
  60. ]\)", a2, b2, c2, d2, e2}]

  62. Jiao[x_, y_, z_] :=
  63. Simplify[((x - y) (z\[Conjugate] - y\[Conjugate]))/((z -
  64.      y) (x\[Conjugate] - y\[Conjugate]))];  (* 定义由 x,y,z 三点构成的有向角 *)
  65. (* 注：上面这个自定义函数，若前面不加Simplify, 运行时间极长，可能做不出来。加上后，全部运行一分钟。 *)
  66. J1 = FunctionExpand[Jiao[a2, c2, b2],
  67.   Element[{a, b, u, v, s, t}, Reals]];  (* \[Angle]A2C2B2 *)
  68. J2 = FunctionExpand[Jiao[a2, d2, b2],
  69.   Element[{a, b, u, v, s, t}, Reals]];  (* \[Angle]A2D2B2 *)
  70. J3 = FunctionExpand[Jiao[a2, e2, b2],
  71.   Element[{a, b, u, v, s, t}, Reals]];  (* \[Angle]A2E2B2 *)
  72. Simplify[{4, "\!\(\*
  73. StyleBox["三个角度",\nFontSize->10,\nFontColor->RGBColor[1, 0, \
  74. 0]]\)\!\(\*
  75. StyleBox["\[Angle]A2C2B2",\nFontColor->RGBColor[0, 0, 1]]\)\!\(\*
  76. StyleBox["，",\nFontColor->RGBColor[0, 0, 1]]\)\!\(\*
  77. StyleBox["\[Angle]A2D2B2",\nFontColor->RGBColor[0, 0, 1]]\)\!\(\*
  78. StyleBox["，",\nFontColor->RGBColor[0, 0, 1]]\)\!\(\*
  79. StyleBox["\[Angle]A2E2B2",\nFontColor->RGBColor[0, 0, 1]]\)\!\(\*
  80. StyleBox["：",\nFontColor->RGBColor[0, 0, 1]]\)", J1, J2, J3}]

  82. If[Simplify[J1 - J2] == 0  && Simplify[J1 - J3] == 0, Print["\!\(\*
  83. StyleBox["由于",\nFontSize->10,\nFontColor->RGBColor[1, 0, 0]]\)\!\(\*
  84. StyleBox["\[Angle]A2C2B2",\nFontColor->RGBColor[0, 0, 1]]\)\!\(\*
  85. StyleBox[" ",\nFontColor->RGBColor[0, 0, 1]]\)\!\(\*
  86. StyleBox["=",\nFontColor->RGBColor[0, 0, 1]]\)\!\(\*
  87. StyleBox[" ",\nFontColor->RGBColor[0, 0, 1]]\)\!\(\*
  88. StyleBox["\[Angle]A2D2B2",\nFontColor->RGBColor[0, 0, 1]]\)\!\(\*
  89. StyleBox[" ",\nFontColor->RGBColor[0, 0, 1]]\)\!\(\*
  90. StyleBox["=",\nFontColor->RGBColor[0, 0, 1]]\)\!\(\*
  91. StyleBox[" ",\nFontColor->RGBColor[0, 0, 1]]\)\!\(\*
  92. StyleBox["\[Angle]A2E2B2",\nFontColor->RGBColor[0, 0, 1]]\)\!\(\*
  93. StyleBox[",",\nFontColor->RGBColor[1, 0, 0]]\)\!\(\*
  94. StyleBox["故",\nFontSize->10,\nFontColor->RGBColor[1, 0, 0]]\)\!\(\*
  95. StyleBox[" ",\nFontSize->10,\nFontColor->RGBColor[1, 0, 0]]\)\!\(\*
  96. StyleBox["A2",\nFontSize->10,\nFontColor->RGBColor[1, 0, 0]]\)\!\(\*
  97. StyleBox[",",\nFontSize->10,\nFontColor->RGBColor[1, 0, 0]]\)\!\(\*
  98. StyleBox["B2",\nFontSize->10,\nFontColor->RGBColor[1, 0, 0]]\)\!\(\*
  99. StyleBox[",",\nFontSize->10,\nFontColor->RGBColor[1, 0, 0]]\)\!\(\*
  100. StyleBox["C2",\nFontSize->10,\nFontColor->RGBColor[1, 0, 0]]\)\!\(\*
  101. StyleBox[",",\nFontSize->10,\nFontColor->RGBColor[1, 0, 0]]\)\!\(\*
  102. StyleBox["D2",\nFontSize->10,\nFontColor->RGBColor[1, 0, 0]]\)\!\(\*
  103. StyleBox[",",\nFontSize->10,\nFontColor->RGBColor[1, 0, 0]]\)\!\(\*
  104. StyleBox["E2",\nFontSize->10,\nFontColor->RGBColor[1, 0, 0]]\)\!\(\*
  105. StyleBox[" ",\nFontSize->10,\nFontColor->RGBColor[1, 0, 0]]\)\!\(\*
  106. StyleBox["五点共圆",\nFontSize->10,\nFontColor->RGBColor[1, 0, 0]]\)"]]
复制代码


程序运行近一分钟，给出如下证明：

五点共圆运行结果.png

程序代码复制以后，许多语句都改变格式了，看不懂了。有办法么？
毋因群疑而阻独见　　毋任己意而废人言
毋私小惠而伤大体　　毋借公论以快私情
回复

使用道具 举报

mathematica
发表于 2017-5-24 13:50:16 | 显示全部楼层
可以给程序多加点注释,容易看明白,我觉得五点共圆很有意思
毋因群疑而阻独见　　毋任己意而废人言
毋私小惠而伤大体　　毋借公论以快私情
回复 支持 反对

使用道具 举报

mathematica
发表于 2017-5-24 13:51:30 | 显示全部楼层
机器证明很有价值,能节省脑力,几何问题代数化,有意思
毋因群疑而阻独见　　毋任己意而废人言
毋私小惠而伤大体　　毋借公论以快私情
回复 支持 反对

使用道具 举报

TSC999
 楼主| 发表于 2017-5-24 22:30:56 | 显示全部楼层
这个机器证明的思路是向李涛学来的。李涛的导师是张景中。李涛作了一套机器证明的软件，这软件我是不知道的，但是软件的原理就体现在上面这个程序设计。
机器证明的难点，一是如何构图，构图要使得各关键点的坐标容易算出。第二，要积累一些平面几何的公式。第三，软件平台是 mathematica，软件的计算能力应该足够强大。
毋因群疑而阻独见　　毋任己意而废人言
毋私小惠而伤大体　　毋借公论以快私情
回复 支持 反对

使用道具 举报

chyanog
发表于 2017-6-15 11:21:29 | 显示全部楼层
本帖最后由 chyanog 于 2017-6-15 11:37 编辑

2017-06-15_111719.png
做过五点共圆这个，没有用复数，Mathematica11计算耗时不到4秒
  1. Clear["`*"];

  3. lineIntersection[{{x1_,y1_},{x2_,y2_},{x3_,y3_},{x4_,y4_}}]=
  4.   Solve[{Det[{{x,y,1},{x1,y1,1},{x2,y2,1}}],Det[{{x,y,1},{x3,y3,1},{x4,y4,1}}]}==0,{x,y}]//First//Values;

  6. reflect[{{x0_,y0_},{x1_,y1_},{x2_,y2_}}]=
  7.   Solve[{Det[{{x1,y1,1},{x2,y2,1},{(x0+x)/2,(y0+y)/2,1}}],({x,y}-{x0,y0}).({x1,y1}-{x2,y2})}==0,{x,y}]//First//Values;

  9. threePointCircle[p_]:=Circumsphere[p]//First;

  11. fourPointOnCircle[{{x1_, y1_}, {x2_, y2_}, {x3_, y3_}, {x4_, y4_}}] :=
  12.   Det[{{x1^2+y1^2,x1,y1,1},{x2^2+y2^2,x2,y2,1},{x3^2+y3^2,x3,y3,1},{x4^2+y4^2,x4,y4,1}}]==0//Simplify;

  14. {B1,B2,B3,B4,B5}={{0,0},{x1,y1},{x2,y2},{x3,y3},{1,0}};
  15. {A1,A2,A3,A4,A5}=lineIntersection/@{{B1,B2,B4,B5},{B1,B5,B2,B3},{B1,B2,B3,B4},{B2,B3,B4,B5},{B1,B5,B3,B4}};
  16. {O1,O2,O3,O4,O5}=threePointCircle/@{{A1,B1,B5},{A2,B1,B2},{A3,B2,B3},{A4,B3,B4},{A5,B4,B5}}; (*五三角形的外心坐标*)
  17. {C1,C2,C3,C4,C5}=reflect/@{{B1,O1,O2},{B2,O2,O3},{B3,O3,O4},{B4,O4,O5},{B5,O5,O1}}//Simplify; (*五圆外侧交点坐标*)

  19. fourPointOnCircle[{C1,C2,C3,C4}]
  20. fourPointOnCircle[{C2,C3,C4,C5}]
复制代码
毋因群疑而阻独见　　毋任己意而废人言
毋私小惠而伤大体　　毋借公论以快私情
回复 支持 反对

使用道具 举报

mathematica
发表于 2021-6-18 09:30:40 | 显示全部楼层
chyanog 发表于 2017-6-15 11:21
做过五点共圆这个，没有用复数，Mathematica11计算耗时不到4秒

思路在哪里？最好要有思路
毋因群疑而阻独见　　毋任己意而废人言
毋私小惠而伤大体　　毋借公论以快私情
回复 支持 反对

使用道具 举报

dlsh
发表于 2021-6-18 21:23:32 | 显示全部楼层
In[1]:= Clear["`*"];

lineIntersection[{{x1_, y1_}, {x2_, y2_}, {x3_, y3_}, {x4_, y4_}}] =
  Solve[{Det[{{x, y, 1}, {x1, y1, 1}, {x2, y2, 1}}],
       Det[{{x, y, 1}, {x3, y3, 1}, {x4, y4, 1}}]} == 0, {x, y}] //
    First // Values;

reflect[{{x0_, y0_}, {x1_, y1_}, {x2_, y2_}}] =
  Solve[{Det[{{x1, y1, 1}, {x2, y2, 1}, {(x0 + x)/2, (y0 + y)/2,
          1}}], ({x, y} - {x0, y0}).({x1, y1} - {x2, y2})} == 0, {x,
      y}] // First // Values;

threePointCircle[p_] := Circumsphere[p] // First;

fourPointOnCircle[{{x1_, y1_}, {x2_, y2_}, {x3_, y3_}, {x4_, y4_}}] :=
   Det[{{x1^2 + y1^2, x1, y1, 1}, {x2^2 + y2^2, x2, y2,
       1}, {x3^2 + y3^2, x3, y3, 1}, {x4^2 + y4^2, x4, y4, 1}}] == 0 //
    Simplify;

{B1, B2, B3, B4, B5} = {{0, 0}, {x1, y1}, {x2, y2}, {x3, y3}, {1, 0}};
{A1, A2, A3, A4, A5} =
  lineIntersection /@ {{B1, B2, B4, B5}, {B1, B5, B2, B3}, {B1, B2,
     B3, B4}, {B2, B3, B4, B5}, {B1, B5, B3, B4}};
{O1, O2, O3, O4, O5} =
threePointCircle /@ {{A1, B1, B5}, {A2, B1, B2}, {A3, B2, B3}, {A4,
    B3, B4}, {A5, B4, B5}};(*五三角形的外心坐标*){C1, C2, C3, C4, C5} =
reflect /@ {{B1, O1, O2}, {B2, O2, O3}, {B3, O3, O4}, {B4, O4,
     O5}, {B5, O5, O1}} // Simplify;(*五圆外侧交点坐标*)fourPointOnCircle[{C1,
   C2, C3, C4}]
fourPointOnCircle[{C2, C3, C4, C5}]

Out[8]= True

Out[9]= True
没有输出具体数值
毋因群疑而阻独见　　毋任己意而废人言
毋私小惠而伤大体　　毋借公论以快私情
回复 支持 反对

使用道具 举报

彭翕成
发表于 2021-6-20 16:18:22 | 显示全部楼层
dlsh 发表于 2021-6-18 21:23
In[1]:= Clear["`*"];

lineIntersection[{{x1_, y1_}, {x2_, y2_}, {x3_, y3_}, {x4_, y4_}}] =

去掉几个分号即可。想看哪几个点，就去掉该行后面的分号
毋因群疑而阻独见　　毋任己意而废人言
毋私小惠而伤大体　　毋借公论以快私情
回复 支持 反对

使用道具 举报

dlsh
发表于 2021-6-20 21:45:16 | 显示全部楼层
本帖最后由 dlsh 于 2021-6-20 21:46 编辑

谢谢老师，看到了
毋因群疑而阻独见　　毋任己意而废人言
毋私小惠而伤大体　　毋借公论以快私情
回复 支持 反对

使用道具 举报

返回列表 发新帖
高级模式
B Color Image Link Quote Code Smilies
您需要登录后才可以回帖 登录 | 欢迎注册

本版积分规则

小黑屋|手机版|数学研发网 ( 苏ICP备07505100号 )

GMT+8, 2024-11-23 16:03 , Processed in 0.026917 second(s), 20 queries .

Powered by Discuz! X3.5

© 2001-2024 Discuz! Team.

快速回复 返回顶部 返回列表