mathematica 机器证明平面几何定理【例 3】

TSC999 · 发表于 2017-5-24 22:47:25

马上注册，结交更多好友，享用更多功能，让你轻松玩转社区。

您需要登录才可以下载或查看，没有账号？欢迎注册

×

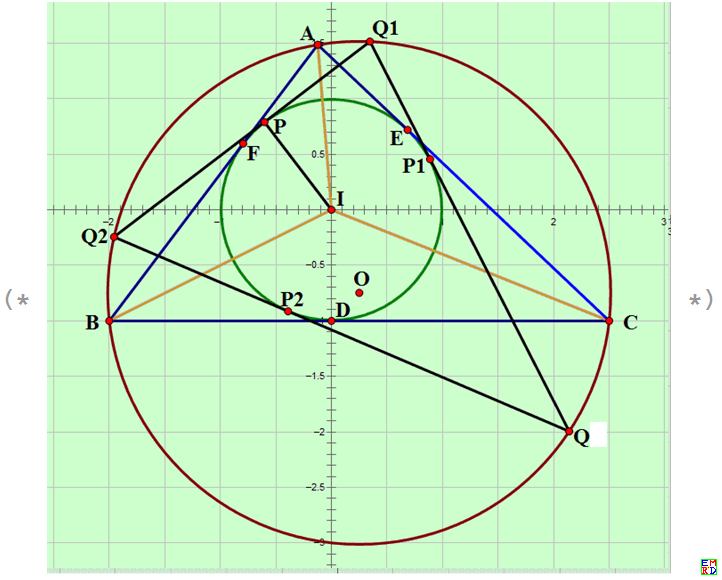
彭色列定理的最简单情况：从三角形 ABC 的外接圆上任意一点 $ Q $作内切圆的两条切线，设它们分别交外接圆于点$ Q1 $和$ Q2 $，则$ Q1Q2 $ 也是内切圆的切线（如上图）。

程序如下：

XI = 0; YI = 0; (* 令三角形内切圆的半径为 1, 圆心位于坐标系原点 *)
ZI = XI + YI I; (* 三角形内切圆圆心 I 的复坐标 *)
u =.; v =.;
XB = u; YB = -1; XC = v; YC = -1; (* 定义 B、C 点的坐标。BC 平行于横轴。u, v \
是独立变量，u<0, v>0 *)
ZB = XB + YB I; ZC = XC + YC I; (* B、C 点的复坐标 *)
(* 下面求 A 点的坐标 *)
XA =.; YA =.; aa = {XA, YA} /.
Assuming[XA (YB - YC) + XB (YC - YA) + XC (YA - YB) > 0 ,
Solve[{(XA Sqrt[(XB - XC)^2 + (YB - YC)^2] +
XB Sqrt[(XA - XC)^2 + (YA - YC)^2] +
XC Sqrt[(XA - XB)^2 + (YA - YB)^2])/(
Sqrt[(XA - XB)^2 + (YA - YB)^2] +
Sqrt[(XB - XC)^2 + (YB - YC)^2] +
Sqrt[(XC - XA)^2 + (YC - YA)^2]) == 0, (
YA Sqrt[(XB - XC)^2 + (YB - YC)^2] +
YB Sqrt[(XA - XC)^2 + (YA - YC)^2] +
YC Sqrt[(XA - XB)^2 + (YA - YB)^2])/(
Sqrt[(XA - XB)^2 + (YA - YB)^2] +
Sqrt[(XB - XC)^2 + (YB - YC)^2] +
Sqrt[(XC - XA)^2 + (YC - YA)^2]) == 0, (
XA (YB - YC) + XB (YC - YA) + XC (YA - YB))/(
Sqrt[(XA - XB)^2 + (YA - YB)^2] +
Sqrt[(XB - XC)^2 + (YB - YC)^2] +
Sqrt[(XC - XA)^2 + (YC - YA)^2]) == 1}, {XA, YA }]];
bb = aa[[1]];
XA = bb[[1]]; (* A 点的横坐标 *)
YA = bb[[2]]; (* A 点的纵坐标 *)
ZA = Simplify[XA + YA I]; (* A 点的复坐标 *)
Print["\!\(\*
StyleBox["程序给出的证明如下",\nFontColor->RGBColor[0, 0, 1]]\)\!\(\*
StyleBox["：",\nFontColor->RGBColor[0, 0, 1]]\) "];
Print["\!\(\*
StyleBox["\[EmptyUpTriangle]ABC",\nFontColor->RGBColor[0, 0, \
1]]\)\!\(\*
StyleBox[" ",\nFontColor->RGBColor[0, 0, 1]]\)\!\(\*
StyleBox["各顶点的复坐标",\nFontColor->RGBColor[0, 0, 1]]\)\!\(\*
StyleBox["：",\nFontColor->RGBColor[0, 0, 1]]\) "];
Print["A = ", ZA];
ZB = Simplify[XB + YB I]; (* B 点的复坐标 *)
Print["B = ", ZB];
ZC = Simplify[XC + YC I]; (* C 点的复坐标 *)
Print["C = ", ZC];
(* 三角形 ABC 外接圆圆心 O 的坐标： *)
XO = ((XA^2 (YB - YC) + XB^2 ( YC - YA) +
XC^2 ( YA - YB)) - (YA - YB ) ( YB - YC) (YC - YA))/(
2 XA (YB - YC) + 2 XB ( YC - YA) + 2 XC ( YA - YB));
YO = -(((YA^2 (XB - XC) + YB^2 ( XC - XA) +
YC^2 ( XA - XB)) - (XA - XB ) ( XB - XC) (XC - XA))/(
2 XA (YB - YC) + 2 XB ( YC - YA) + 2 XC ( YA - YB)));
ZO = Factor[XO + YO I];
Print["\!\(\*
StyleBox["\[EmptyUpTriangle]ABC",\nFontColor->RGBColor[0, 0, \
1]]\)\!\(\*
StyleBox[" ",\nFontColor->RGBColor[0, 0, 1]]\)\!\(\*
StyleBox["外接圆圆心的复坐标",\nFontColor->RGBColor[0, 0, 1]]\)\!\(\*
StyleBox["：",\nFontColor->RGBColor[0, 0, 1]]\) "];
Print["O = ", ZO];
(* 下面求三角形 ABC 外接圆的半径 R *)
R = Assuming[u < 0 && v > 0 && 1 + u v < 0,
Factor[Simplify[
Sqrt[((XA - XB)^2 + (YA - YB)^2) ((XB - XC)^2 + (YB -
YC)^2) ((XC - XA)^2 + (YC - YA)^2)]/(
2 (XA (YB - YC) + XB (YC - YA) + XC (YA - YB)))]]];
Print["\!\(\*
StyleBox["\[EmptyUpTriangle]ABC",\nFontColor->RGBColor[0, 0, \
1]]\)\!\(\*
StyleBox[" ",\nFontColor->RGBColor[0, 0, 1]]\)\!\(\*
StyleBox["外接圆的半径",\nFontColor->RGBColor[0, 0, 1]]\)\!\(\*
StyleBox["：",\nFontColor->RGBColor[0, 0, 1]]\) "];
Print["R = ", R];
\[Alpha] =.; (* 在内切圆 I 上任取一点 P, IP 直线与横轴的夹角为 \[Alpha] *)
XP = Cos[\[Alpha]]; YP = Sin[\[Alpha]] ;
ZP = Factor[XP + YP I]; (* P 点的复坐标 *)
Print["\!\(\*
StyleBox["在内切圆",\nFontColor->RGBColor[0, 0, 1]]\) \!\(\*
StyleBox["I",\nFontColor->RGBColor[0, 0, 1]]\)\!\(\*
StyleBox[" ",\nFontColor->RGBColor[0, 0, 1]]\)\!\(\*
StyleBox["上任取一点",\nFontColor->RGBColor[0, 0, 1]]\)\!\(\*
StyleBox[" ",\nFontColor->RGBColor[0, 0, 1]]\)\!\(\*
StyleBox["P",\nFontColor->RGBColor[0, 0, 1]]\)\!\(\*
StyleBox[",",\nFontColor->RGBColor[0, 0, 1]]\)\!\(\*
StyleBox[" ",\nFontColor->RGBColor[0, 0, 1]]\)\!\(\*
StyleBox["IP",\nFontColor->RGBColor[0, 0, 1]]\)\!\(\*
StyleBox[" ",\nFontColor->RGBColor[0, 0, 1]]\)\!\(\*
StyleBox["与横轴的夹角为\[Alpha]",\nFontColor->RGBColor[0, 0, 1]]\)\!\(\*
StyleBox[" ",\nFontColor->RGBColor[0, 0, 1]]\)\!\(\*
StyleBox["时",\nFontColor->RGBColor[0, 0, 1]]\)\!\(\*
StyleBox["，",\nFontColor->RGBColor[0, 0, 1]]\)\!\(\*
StyleBox["P",\nFontColor->RGBColor[0, 0, 1]]\)\!\(\*
StyleBox[" ",\nFontColor->RGBColor[0, 0, 1]]\)\!\(\*
StyleBox["点的复坐标",\nFontColor->RGBColor[0, 0, 1]]\)\!\(\*
StyleBox["：",\nFontColor->RGBColor[0, 0, 1]]\) "];
Print["P = ", ZP];
(* 自 P 点作圆 I 的切线，交圆 O 于 Q1 和 Q2,下面求 Q1 及 Q2 的坐标 *)
(* Q1Q2 直线的方程是 x Cos[\[Alpha]]+y Sin[\[Alpha]]=1, 三角形 ABC 外接圆的方程是 \
(x-XO)^2+(y-YO)^2= R^2 *)
x =.; y =.; aa = {{x, y}} /.
Simplify[Assuming[u < 0 && v > 0 && 1 + u v < 0,
Solve[{x Cos[\[Alpha]] + y Sin[\[Alpha]] ==
1, (x - XO)^2 + (y - YO)^2 == R^2}, {Factor[Simplify[x]],
Factor[Simplify[y]] }]]];
bb1 = aa[[1]];(* 交点 Q2 *)
bb2 = aa[[2]];(* 交点 Q1 *)
cc1 = bb1[[1]]; XQ2 = cc1[[1]]; YQ2 = cc1[[2]];
cc2 = bb2[[1]]; XQ1 = cc2[[1]]; YQ1 = cc2[[2]];
ZQ1 = Simplify[XQ1 + YQ1 I];
ZQ2 = Simplify[XQ2 + YQ2 I] ;
Print["\!\(\*
StyleBox["自",\nFontColor->RGBColor[0, 0, 1]]\)\!\(\*
StyleBox[" ",\nFontColor->RGBColor[0, 0, 1]]\)\!\(\*
StyleBox["P",\nFontColor->RGBColor[0, 0, 1]]\)\!\(\*
StyleBox[" ",\nFontColor->RGBColor[0, 0, 1]]\)\!\(\*
StyleBox["点作圆",\nFontColor->RGBColor[0, 0, 1]]\)\!\(\*
StyleBox[" ",\nFontColor->RGBColor[0, 0, 1]]\)\!\(\*
StyleBox["I",\nFontColor->RGBColor[0, 0, 1]]\)\!\(\*
StyleBox[" ",\nFontColor->RGBColor[0, 0, 1]]\)\!\(\*
StyleBox["的切线",\nFontColor->RGBColor[0, 0, 1]]\)\!\(\*
StyleBox["，",\nFontColor->RGBColor[0, 0, 1]]\)\!\(\*
StyleBox["交\[EmptyUpTriangle]ABC",\nFontColor->RGBColor[0, 0, 1]]\)\
\!\(\*
StyleBox[" ",\nFontColor->RGBColor[0, 0, 1]]\)\!\(\*
StyleBox["外接圆于",\nFontColor->RGBColor[0, 0, 1]]\)\!\(\*
StyleBox[" ",\nFontColor->RGBColor[0, 0, 1]]\)\!\(\*
StyleBox["Q1",\nFontColor->RGBColor[0, 0, 1]]\)\!\(\*
StyleBox[" ",\nFontColor->RGBColor[0, 0, 1]]\)\!\(\*
StyleBox["和",\nFontColor->RGBColor[0, 0, 1]]\)\!\(\*
StyleBox[" ",\nFontColor->RGBColor[0, 0, 1]]\)\!\(\*
StyleBox["Q2",\nFontColor->RGBColor[0, 0, 1]]\)\!\(\*
StyleBox[",",\nFontColor->RGBColor[0, 0, 1]]\)\!\(\*
StyleBox["则",\nFontColor->RGBColor[0, 0, 1]]\)\!\(\*
StyleBox[" ",\nFontColor->RGBColor[0, 0, 1]]\)\!\(\*
StyleBox["Q1",\nFontColor->RGBColor[0, 0, 1]]\)\!\(\*
StyleBox[" ",\nFontColor->RGBColor[0, 0, 1]]\)\!\(\*
StyleBox["及",\nFontColor->RGBColor[0, 0, 1]]\)\!\(\*
StyleBox[" ",\nFontColor->RGBColor[0, 0, 1]]\)\!\(\*
StyleBox["Q2",\nFontColor->RGBColor[0, 0, 1]]\)\!\(\*
StyleBox[" ",\nFontColor->RGBColor[0, 0, 1]]\)\!\(\*
StyleBox["的复坐标为",\nFontColor->RGBColor[0, 0, 1]]\)\!\(\*
StyleBox["：",\nFontColor->RGBColor[0, 0, 1]]\) "];
Print["Q1 = ", ZQ1];
Print["Q2 = ", ZQ2];
(* 从 Q1 向单位圆 I 作切线，交 \[CircleDot]O 于 Q 点。则该切线的方程是
(XP XQ1^2+2 XQ1 YP YQ1-XP YQ1^2)x+ (YP YQ1^2+2YQ1 XP XQ1-YP XQ1^2 \
)y =XQ1^2+YQ1^2
从 Q2 向单位圆 I 作切线，交 \[CircleDot]O 于 Q 点。则该切线的方程是
(XP XQ2^2+2 XQ2 YP YQ2-XP YQ2^2)x+ (YP YQ2^2+2YQ2 XP XQ2-YP XQ2^2 )y \
=XQ2^2+YQ2^2
下面求上述两条切线的交点 Q 的坐标 *)
x =.; y =.; aa = {{x, y}} /.
Simplify[Assuming[u < 0 && v > 0 && 1 + u v < 0,
Solve[{(XP XQ1^2 + 2 XQ1 YP YQ1 - XP YQ1^2) x + (YP YQ1^2 +
2 YQ1 XP XQ1 - YP XQ1^2 ) y ==
XQ1^2 + YQ1^2, (XP XQ2^2 + 2 XQ2 YP YQ2 -
XP YQ2^2) x + (YP YQ2^2 +2 YQ2 XP XQ2 -YP XQ2^2 ) y ==
XQ2^2 + YQ2^2}, {Factor[Simplify[x]], Factor[Simplify[y]] }]]];
bb = aa[[1]];(* 交点 Q *)
cc = bb[[1]];
XQ = cc[[1]];
YQ = cc[[2]];
ZQ = Simplify[XQ + YQ I]; (* 交点 Q 的复坐标 *)
Print["\!\(\*
StyleBox["从",\nFontColor->RGBColor[0, 0, 1]]\)\!\(\*
StyleBox[" ",\nFontColor->RGBColor[0, 0, 1]]\)\!\(\*
StyleBox["Q1",\nFontColor->RGBColor[0, 0, 1]]\)\!\(\*
StyleBox[" ",\nFontColor->RGBColor[0, 0, 1]]\)\!\(\*
StyleBox["和",\nFontColor->RGBColor[0, 0, 1]]\)\!\(\*
StyleBox[" ",\nFontColor->RGBColor[0, 0, 1]]\)\!\(\*
StyleBox["Q2",\nFontColor->RGBColor[0, 0, 1]]\)\!\(\*
StyleBox[" ",\nFontColor->RGBColor[0, 0, 1]]\)\!\(\*
StyleBox["分别向",\nFontColor->RGBColor[0, 0, 1]]\)\!\(\*
StyleBox[" ",\nFontColor->RGBColor[0, 0, 1]]\)\!\(\*
StyleBox["\[CircleDot]",\nFontColor->RGBColor[0, 0, 1]]\)\!\(\*
StyleBox["I",\nFontColor->RGBColor[0, 0, 1]]\)\!\(\*
StyleBox[" ",\nFontColor->RGBColor[0, 0, 1]]\)\!\(\*
StyleBox["作切线",\nFontColor->RGBColor[0, 0, 1]]\)\!\(\*
StyleBox["，",\nFontColor->RGBColor[0, 0, 1]]\)\!\(\*
StyleBox["两条切线相交于",\nFontColor->RGBColor[0, 0, 1]]\)\!\(\*
StyleBox[" ",\nFontColor->RGBColor[0, 0, 1]]\)\!\(\*
StyleBox["Q",\nFontColor->RGBColor[0, 0, 1]]\)\!\(\*
StyleBox[" ",\nFontColor->RGBColor[0, 0, 1]]\)\!\(\*
StyleBox["点",\nFontColor->RGBColor[0, 0, 1]]\)\!\(\*
StyleBox["。",\nFontColor->RGBColor[0, 0, 1]]\)\!\(\*
StyleBox[" ",\nFontColor->RGBColor[0, 0, 1]]\)\!\(\*
StyleBox["则",\nFontColor->RGBColor[0, 0, 1]]\)\!\(\*
StyleBox[" ",\nFontColor->RGBColor[0, 0, 1]]\)\!\(\*
StyleBox["Q",\nFontColor->RGBColor[0, 0, 1]]\)\!\(\*
StyleBox[" ",\nFontColor->RGBColor[0, 0, 1]]\)\!\(\*
StyleBox["点的复坐标为",\nFontColor->RGBColor[0, 0, 1]]\)\!\(\*
StyleBox["：",\nFontColor->RGBColor[0, 0, 1]]\) "];
Print["Q = ", ZQ];
(* 下面验证 A、B、C、Q 四点是否共圆。若四个点的复坐标分别是 Z1,Z2,Z3,Z4, 则这四点共圆的充要条件是
\[OpenCurlyDoubleQuote]交比\[CloseCurlyDoubleQuote] \
Z=((Z1-Z3)(Z2-Z4))/((Z1-Z4)(Z2-Z3)) 的虚部等于零，或者说 Z 是一个实数。 *)
Z0 = Factor[
Simplify[((ZA - ZC) (ZB - ZQ))/((ZA - ZQ) (ZB -
ZC))]]; (* 计算 A、B、C、Q 四点的交比 *)
Print["\!\(\*
StyleBox["下面验证",\nFontColor->RGBColor[0, 0, 1]]\)\!\(\*
StyleBox[" ",\nFontColor->RGBColor[0, 0, 1]]\)\!\(\*
StyleBox["Q",\nFontColor->RGBColor[0, 0, 1]]\)\!\(\*
StyleBox[" ",\nFontColor->RGBColor[0, 0, 1]]\)\!\(\*
StyleBox["点是否在",\nFontColor->RGBColor[0, 0, 1]]\)\!\(\*
StyleBox[" ",\nFontColor->RGBColor[0, 0, 1]]\)\!\(\*
StyleBox["\[EmptyUpTriangle]ABC",\nFontColor->RGBColor[0, 0, \
1]]\)\!\(\*
StyleBox[" ",\nFontColor->RGBColor[0, 0, 1]]\)\!\(\*
StyleBox["的外接圆上",\nFontColor->RGBColor[0, 0, 1]]\)\!\(\*
StyleBox["。",\nFontColor->RGBColor[0, 0, 1]]\)\!\(\*
StyleBox[" ",\nFontColor->RGBColor[0, 0, 1]]\)\!\(\*
StyleBox["为此须计算",\nFontColor->RGBColor[0, 0, 1]]\)\!\(\*
StyleBox[" ",\nFontColor->RGBColor[0, 0, 1]]\)\!\(\*
StyleBox["A",\nFontColor->RGBColor[0, 0, 1]]\)\!\(\*
StyleBox["、",\nFontColor->RGBColor[0, 0, 1]]\)\!\(\*
StyleBox["B",\nFontColor->RGBColor[0, 0, 1]]\)\!\(\*
StyleBox["、",\nFontColor->RGBColor[0, 0, 1]]\)\!\(\*
StyleBox["C",\nFontColor->RGBColor[0, 0, 1]]\)\!\(\*
StyleBox["、",\nFontColor->RGBColor[0, 0, 1]]\)\!\(\*
StyleBox["Q",\nFontColor->RGBColor[0, 0, 1]]\)\!\(\*
StyleBox[" ",\nFontColor->RGBColor[0, 0, 1]]\)\!\(\*
StyleBox["四点复坐标的交比",\nFontColor->RGBColor[0, 0, 1]]\)\!\(\*
StyleBox["。",\nFontColor->RGBColor[0, 0, 1]]\) "];
Print["Z0 = ", Z0];
(* 判断交比的虚部是否等于零。若等于零，则 A、B、C、Q 四点共圆。 *)
If[Factor[ComplexExpand[Im[Z0]]] == 0 ,
Print["\!\(\*
StyleBox["由于交比",\nFontColor->RGBColor[0, 0, 1]]\)\!\(\*
StyleBox[" ",\nFontColor->RGBColor[0, 0, 1]]\)\!\(\*
StyleBox["Z0",\nFontColor->RGBColor[0, 0, 1]]\)\!\(\*
StyleBox[" ",\nFontColor->RGBColor[0, 0, 1]]\)\!\(\*
StyleBox["的虚部等于零",\nFontColor->RGBColor[0, 0, 1]]\)\!\(\*
StyleBox["，",\nFontColor->RGBColor[0, 0, 1]]\)\!\(\*
StyleBox["所以",\nFontColor->RGBColor[0, 0, 1]]\)\!\(\*
StyleBox[" ",\nFontColor->RGBColor[0, 0, 1]]\)\!\(\*
StyleBox["A",\nFontColor->RGBColor[0, 0, 1]]\)\!\(\*
StyleBox[",",\nFontColor->RGBColor[0, 0, 1]]\)\!\(\*
StyleBox["B",\nFontColor->RGBColor[0, 0, 1]]\)\!\(\*
StyleBox[",",\nFontColor->RGBColor[0, 0, 1]]\)\!\(\*
StyleBox["C",\nFontColor->RGBColor[0, 0, 1]]\)\!\(\*
StyleBox[",",\nFontColor->RGBColor[0, 0, 1]]\)\!\(\*
StyleBox["Q",\nFontColor->RGBColor[0, 0, 1]]\)\!\(\*
StyleBox[" ",\nFontColor->RGBColor[0, 0, 1]]\)\!\(\*
StyleBox["四点共圆",\nFontColor->RGBColor[0, 0, 1]]\)\!\(\*
StyleBox["，",\nFontColor->RGBColor[0, 0, 1]]\)\!\(\*
StyleBox["这就证明了彭色列定理成立",\nFontColor->RGBColor[0, 0, 1]]\)\!\(\*
StyleBox["。",\nFontColor->RGBColor[0, 0, 1]]\)"]];

复制代码

TSC999 · 发表于 2017-5-24 22:54:05

这个程序大约运行了 20 多秒吧。

mathematica · 发表于 2021-6-18 09:27:39

这个定理看起来不错，不过我肯定是不会证明的！

账号		自动登录	找回密码
密码			欢迎注册

[分享] mathematica 机器证明平面几何定理【例 3】

马上注册，结交更多好友，享用更多功能，让你轻松玩转社区。