一圆绕一定椭圆滚动，圆心轨迹方程是什么？

数学星空

对于22#的三个条件:
若不考虑(3),即$t0=t$我们可以得到关于圆心$(x0,y0)$的轨迹方程
$6*a^4*x0^4*b^4-2*b^6*y0^2*r^4+6*a^4*x0^2*b^6+a^4*x0^4*y0^4+a^4*x0^4*r^4+b^4*y0^4*x0^4+6*b^6*x0^2*r^4+b^4*y0^4*r^4+$
$2*a^6*b^4*r^2-2*b^8*r^2*x0^2+6*b^4*y0^4*a^4+6*a^6*r^4*y0^2-2*b^2*y0^2*a^8-2*x0^2*b^8*a^2-4*a^6*x0^2*b^4+6*b^4*y0^2*a^6-$
$6*b^2*y0^4*a^6-4*b^6*y0^2*a^4-6*x0^4*a^2*b^6+2*a^2*b^4*r^6-2*a^6*x0^2*y0^4-2*b^4*y0^2*r^6-2*b^6*y0^2*x0^4+2*b^4*y0^2*x0^6+$
$2*a^4*b^2*r^6-4*b^4*x0^2*r^6+6*b^4*x0^4*r^4-6*b^6*x0^4*r^2-4*b^4*x0^6*r^2-2*r^6*a^4*x0^2-2*r^4*a^6*x0^2-6*a^6*r^2*y0^4+$
$2*a^6*b^2*r^4+2*a^2*b^6*r^4-2*a^2*b^8*r^2-2*a^2*b^2*r^8-4*a^2*b^4*x0^6+6*a^4*y0^4*r^4+2*a^4*x0^2*y0^6-4*a^4*b^2*y0^6+$
$2*a^4*b^6*r^2-4*a^4*y0^6*r^2-6*a^4*b^4*r^4-4*a^4*y0^2*r^6-2*a^8*b^2*r^2-$
$2*a^8*y0^2*r^2+b^4*r^8+a^8*b^4+r^8*a^4+a^8*r^4+b^8*a^4+b^8*r^4+a^4*y0^8+a^8*y0^4+b^8*x0^4+b^4*x0^8-2*a^6*b^6-$
$2*r^6*a^6+2*a^6*y0^6-2*b^6*r^6+2*b^6*x0^6-6*a^2*x0^2*b^4*y0^4-$
$6*a^4*x0^4*b^2*y0^2+2*b^4*y0^2*a^2*x0^4+2*b^2*y0^4*a^4*x0^2+4*b^2*y0^4*a^2*x0^4+2*b^2*y0^6*a^2*x0^2+2*b^2*y0^2*x0^6*a^2-$
$2*a^4*x0^4*y0^2*r^2+6*b^2*y0^2*a^6*x0^2+6*b^6*y0^2*a^2*x0^2+4*b^6*y0^2*x0^2*r^2+6*b^4*y0^2*x0^2*r^4-6*b^4*y0^2*x0^4*r^2-$
$10*b^4*y0^2*a^4*x0^2-8*a^2*b^4*x0^2*r^4-6*a^2*b^2*x0^4*r^4+10*a^2*b^4*x0^4*r^2-8*a^4*b^2*y0^2*r^4+4*a^4*b^2*r^4*x0^2-$
$8*a^4*b^4*x0^2*r^2+10*a^4*b^2*y0^4*r^2+6*a^2*b^2*x0^2*r^6+4*a^2*b^6*x0^2*r^2+4*a^2*b^4*y0^2*r^4+2*a^2*b^2*y0^6*r^2+$
$2*a^2*b^2*x0^6*r^2-6*a^2*b^4*y0^4*r^2+6*a^2*b^6*y0^2*r^2+4*a^6*b^2*y0^2*r^2-6*a^2*b^2*y0^4*r^4+6*a^2*b^2*y0^2*r^6-$
$2*b^4*y0^4*x0^2*r^2+4*a^6*x0^2*r^2*y0^2+6*a^6*b^2*x0^2*r^2+6*a^4*r^4*x0^2*y0^2-8*a^4*b^4*y0^2*r^2-6*a^4*b^2*x0^4*r^2-$
$6*a^4*x0^2*r^2*y0^4-6*a^4*b^2*y0^2*x0^2*r^2+2*a^2*b^2*y0^2*x0^4*r^2-10*a^2*b^2*y0^2*r^4*x0^2+2*a^2*b^2*y0^4*r^2*x0^2-$
$6*a^2*b^4*y0^2*x0^2*r^2=0$

取$a=5,b=3,r=2,x0=x,y0=y$,得到
$2822400+612*y^2*x^6-6138*x^6+550*y^6+125641*x^4-2515296*y^2+81*x^8+556690*y^2*x^2-1006240*x^2-308279*y^4+$
$1606*x^4*y^4-45998*x^2*y^4-36302*x^4*y^2+1700*y^6*x^2+625*y^8=0$
画图得到：


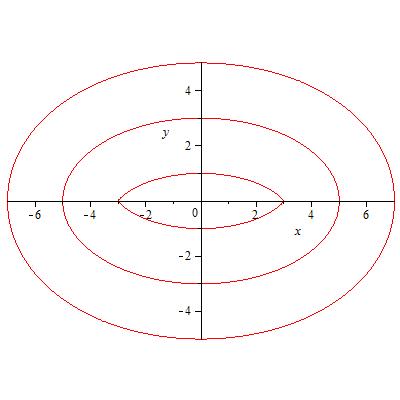和楼上的结论是一致的

数学星空

同理对于双椭圆情形不考虑条件(3)，取$t0=t1=t$
我们可以得到
$6*a^2*s^3*n^2-6*a^2*s^5*n^2+2*a^2*s^7*n^2+8*a^2*s^5*m^2-8*b^2*n^2*s^5-6*b^2*m^2*s^3+6*b^2*m^2*s^5-2*b^2*m^2*s^7-$
$2*a^2*s*n^2-8*a^2*s^3*m^2+8*b^2*n^2*s^3+2*b^2*m^2*s+2*a*s*n^2*x0-2*b*m^2*s*x0-2*a*s^3*n^2*x0-2*a*s^5*n^2*x0+$
$2*a*s^7*n^2*x0-14*a*s^5*n^2*b+4*a*s^6*n^2*y0+8*a*s^5*m^2*x0+14*a*s^5*m^2*b-4*a*s^2*n^2*y0-14*a*s^3*m^2*b-4*a*s^6*m^2*y0+$
$2*b*n^2*s^7*a-2*b*n^2*s^3*x0-2*b*n^2*s^5*x0+2*b*n^2*s^7*x0+4*b*n^2*s^6*y0-2*b*m^2*s^7*a+2*b*m^2*s^3*x0+2*b*m^2*s^5*x0-$
$2*b*m^2*s^7*x0+2*b*m^2*y0*s^2-2*b*m^2*y0*s^6+2*b*n^2*s*x0+4*a*s^2*m^2*y0+8*a*s^3*m^2*x0+14*a*s^3*n^2*b-2*b*n^2*s*a-$
$4*b*n^2*s^2*y0+2*b*m^2*s*a-b*m^2*y0+b*m^2*y0*s^8=0$

$-n^2*m^2*s^8+m^2*y0^2*s^8+n^2*a^2*s^8+n^2*x0^2*s^8+6*n^2*a^2*s^4-$
$4*n^2*a^2*s^6-2*n^2*x0^2*s^4+4*m^2*a^2*s^6-8*m^2*a^2*s^4+4*m^2*a^2*s^2+8*m^2*x0^2*s^4-8*m^2*b^2*s^4-$
$2*m^2*s^4*y0^2+4*m^2*s^2*x0^2+4*m^2*x0^2*s^6+4*m^2*b^2*s^2+4*m^2*b^2*s^6-4*n^2*m^2*s^2-6*n^2*m^2*s^4-$
$4*n^2*m^2*s^6+8*n^2*s^4*y0^2-4*n^2*a^2*s^2+4*n^2*s^2*y0^2+4*n^2*y0^2*s^6+16*n^2*b^2*s^4-2*n^2*a*x0+n^2*a^2+$
$n^2*x0^2+m^2*y0^2-n^2*m^2-4*m^2*a*s*y0+8*m^2*a*b*s^2+4*m^2*a*y0*s^3-4*n^2*a*y0*s^3-8*m^2*a*s^2*x0+4*n^2*a*s^2*x0-$
$16*n^2*b*s^3*y0+8*m^2*x0*s^6*b-4*m^2*b*s*y0-4*m^2*b*s^7*y0+4*m^2*b*s^5*y0+4*m^2*b*s^3*y0-4*m^2*x0*s^7*y0+$
$8*m^2*a*s^6*x0-16*m^2*a*s^4*b+4*m^2*a*s^5*y0+8*m^2*a*s^6*b-4*m^2*a*s^7*y0-8*m^2*x0*b*s^2+4*m^2*x0*s*y0+$
$4*m^2*x0*y0*s^3-8*n^2*x0*s^6*b+4*n^2*a*s*y0+4*n^2*x0*s^7*y0-4*n^2*a*s^6*x0+16*n^2*a*s^4*b-4*n^2*a*s^5*y0+$
$2*n^2*a*s^8*x0-8*n^2*a*s^6*b+4*n^2*a*s^7*y0+8*n^2*x0*b*s^2-4*n^2*x0*s*y0-4*n^2*x0*y0*s^3-4*m^2*x0*s^5*y0-$
$8*n^2*a*b*s^2+4*n^2*x0*s^5*y0-16*n^2*b*s^5*y0=0$

以上两个方程消掉变量s就可以得到椭圆$C_2$中心的轨迹方程．

若取$a=5,b=3,m=2,n=1,x0=x,y0=y$我们可以得到椭圆$C_2$中心的轨迹方程：
$243956966400-297575341056*y^2-6850250*y^10+75625*y^12+58702418496*y^4-5339329440*y^6+262060225*y^8-$
$127818*x^10+9061713*x^8-331422624*x^6+6541448256*x^4+729*x^12-64944552960*x^2+161167860*y^2*x^6+$
$18630*y^2*x^10-1673810*y^8*x^2-2741202*y^2*x^8+63561493632*x^2*y^2-5437315552*x^2*y^4+119845588*y^6*x^2-$
$111402314*y^4*x^4+17819260*y^6*x^4-96809*y^8*x^4+76550*y^10*x^2+6695292*y^4*x^6+129876*y^6*x^6-$
$49401*y^4*x^8-4661176800*x^4*y^2=0$
画图得到：


椭圆$C_2$滚动轨迹图如下：

yinhow

星空，我怀疑你做的图是否是滚动。我用你同样的参数，做的静态和动态图。

yinhow

数学星空

你做的是"不过两个椭圆的周长之比是有理数"
因此看上去比较对称,我是通过数值解得到的,取的两个椭圆的周长并不是有理数,因此不会有问题...

对于31#,32#因为除掉了条件(3),因此并不是严格的"滚动"

liexi20101117

星空版主做的图好美呀。

huangruqi

越算越复杂