- 注册时间
- 2007-12-27
- 最后登录
- 1970-1-1
- 威望
- 星
- 金币
- 枚
- 贡献
- 分
- 经验
- 点
- 鲜花
- 朵
- 魅力
- 点
- 上传
- 次
- 下载
- 次
- 积分
- 49507
- 在线时间
- 小时
|
马上注册,结交更多好友,享用更多功能,让你轻松玩转社区。
您需要 登录 才可以下载或查看,没有账号?欢迎注册
×
贝努利数是数学中一个非常重要的数列,我们可以通过下面方法定义贝努利数:
$\frac{x}{e^x-1} -= \sum_{n=0}^{oo}\frac{B_nx^n}{n!}$
对于上面的定义,简单计算可以知道,对于奇数n,除了n=1,对应的贝努利数都是0,所以通常我们只考虑偶数项的贝努利数。
记得高三的时候,自己看微积分的书,试着将斯泰林公式
$n! = sqrt(2pi)n^{n+1/2}e^{-n+1/(12n)+O(1/n^3)}$
后面的余项进行推导,发现竟然同贝努利数也拉上了关系。
后来在计算贝努利数时,发现它的分母竟然非常规律。
查询http://mathworld.wolfram.com/BernoulliNumber.html可以知道贝努利数前面几个偶数项分别时
B(2)=1/6,B(4)=-1/30,B(6)=1/42,B(8)=-1/30,B(10)=5/66,...
当时我发现了B(2n)的分母可以写成
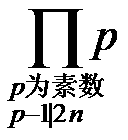 当时好像我还花了很多时间,通过使用二项式证明了上面的结论,但是现在已经不知道当初如何证明的,并且证明过程是否正确。
现在查询一下http://www.research.att.com/~njas/sequences/A002445
可以知道这个结论可以由Von Staudt-Clausen theorem得出。
而非常奇怪的是虽然贝努利数的分母如此规律,但是我们很难找出其分子的规律。
当时好像我还花了很多时间,通过使用二项式证明了上面的结论,但是现在已经不知道当初如何证明的,并且证明过程是否正确。
现在查询一下http://www.research.att.com/~njas/sequences/A002445
可以知道这个结论可以由Von Staudt-Clausen theorem得出。
而非常奇怪的是虽然贝努利数的分母如此规律,但是我们很难找出其分子的规律。 |
|