二次曲面的有理参数表示

creasson

终于得到了任意二次曲面的有理参数表示。

例如单位球 $x^2 + y^2 + z^2 = 1 $
\[x =  - \frac{{3{v^2} - 2v\alpha  - {\alpha ^2} + {u^2}{\alpha ^2} - 4{v^2}\beta  + {v^2}{\beta ^2} - 4{v^2}\alpha \gamma  + 2uv{\alpha ^2}\gamma  + 2{v^2}\alpha \beta \gamma  + 2{v^2}{\alpha ^2}{\gamma ^2}}}{{5{v^2} + 2v\alpha  + {\alpha ^2} + {u^2}{\alpha ^2} - 4{v^2}\beta  + {v^2}{\beta ^2} - 4{v^2}\alpha \gamma  + 2uv{\alpha ^2}\gamma  + 2{v^2}\alpha \beta \gamma  + 2{v^2}{\alpha ^2}{\gamma ^2}}}\]
\[y = \frac{{2\alpha (v + \alpha )(u + v\gamma )}}{{5{v^2} + 2v\alpha  + {\alpha ^2} + {u^2}{\alpha ^2} - 4{v^2}\beta  + {v^2}{\beta ^2} - 4{v^2}\alpha \gamma  + 2uv{\alpha ^2}\gamma  + 2{v^2}\alpha \beta \gamma  + 2{v^2}{\alpha ^2}{\gamma ^2}}}\]
\[z =  - \frac{{2v(v + \alpha )( - 2 + \beta  + \alpha \gamma )}}{{5{v^2} + 2v\alpha  + {\alpha ^2} + {u^2}{\alpha ^2} - 4{v^2}\beta  + {v^2}{\beta ^2} - 4{v^2}\alpha \gamma  + 2uv{\alpha ^2}\gamma  + 2{v^2}\alpha \beta \gamma  + 2{v^2}{\alpha ^2}{\gamma ^2}}}\]

椭圆抛物面 $z = x^2 + y^2 $
\[x =  - \frac{{ - {v^2} - 10v\alpha  + 8uv\alpha  - 5{\alpha ^2} + 5{u^2}{\alpha ^2} - 4{v^2}\beta  - 4uv\alpha \beta  + {v^2}{\beta ^2} + 4{v^2}\alpha \gamma  + 6uv{\alpha ^2}\gamma  - 2{v^2}\alpha \beta \gamma  + 2{v^2}{\alpha ^2}{\gamma ^2}}}{{5{v^2} + 6v\alpha  + 8uv\alpha  + 5{\alpha ^2} + 5{u^2}{\alpha ^2} - 2{v^2}\beta  + 2v\alpha \beta  - 4uv\alpha \beta  + {v^2}{\beta ^2} + 6{v^2}\alpha \gamma  + 2v{\alpha ^2}\gamma  + 6uv{\alpha ^2}\gamma  - 2{v^2}\alpha \beta \gamma  + 2{v^2}{\alpha ^2}{\gamma ^2}}}\]
\[y = \frac{{2(v + \alpha )(4v + 5u\alpha  - 2v\beta  + 3v\alpha \gamma )}}{{5{v^2} + 6v\alpha  + 8uv\alpha  + 5{\alpha ^2} + 5{u^2}{\alpha ^2} - 2{v^2}\beta  + 2v\alpha \beta  - 4uv\alpha \beta  + {v^2}{\beta ^2} + 6{v^2}\alpha \gamma  + 2v{\alpha ^2}\gamma  + 6uv{\alpha ^2}\gamma  - 2{v^2}\alpha \beta \gamma  + 2{v^2}{\alpha ^2}{\gamma ^2}}}\]
\[z = \frac{{13{v^2} + 14v\alpha  + 8uv\alpha  + 5{\alpha ^2} + 5{u^2}{\alpha ^2} - 6{v^2}\beta  - 2v\alpha \beta  - 4uv\alpha \beta  + {v^2}{\beta ^2} + 2{v^2}\alpha \gamma  - 2v{\alpha ^2}\gamma  + 6uv{\alpha ^2}\gamma  - 2{v^2}\alpha \beta \gamma  + 2{v^2}{\alpha ^2}{\gamma ^2}}}{{5{v^2} + 6v\alpha  + 8uv\alpha  + 5{\alpha ^2} + 5{u^2}{\alpha ^2} - 2{v^2}\beta  + 2v\alpha \beta  - 4uv\alpha \beta  + {v^2}{\beta ^2} + 6{v^2}\alpha \gamma  + 2v{\alpha ^2}\gamma  + 6uv{\alpha ^2}\gamma  - 2{v^2}\alpha \beta \gamma  + 2{v^2}{\alpha ^2}{\gamma ^2}}}\]

单叶双曲面 $x^2 + y^2 - z^2 = 1 $

\[x =  - \frac{{ - 8{v^2} - 8v\alpha  - 4{\alpha ^2} + 4{u^2}{\alpha ^2} + 4{v^2}\beta  - {v^2}{\beta ^2} + 4{v^2}\alpha \gamma  + 8uv{\alpha ^2}\gamma  - 2{v^2}\alpha \beta \gamma  + 3{v^2}{\alpha ^2}{\gamma ^2}}}{{8v\alpha  + 4{\alpha ^2} + 4{u^2}{\alpha ^2} + 4{v^2}\beta  - {v^2}{\beta ^2} + 4{v^2}\alpha \gamma  + 8uv{\alpha ^2}\gamma  - 2{v^2}\alpha \beta \gamma  + 3{v^2}{\alpha ^2}{\gamma ^2}}}\]
\[y = \frac{{8\alpha (v + \alpha )(u + v\gamma )}}{{8v\alpha  + 4{\alpha ^2} + 4{u^2}{\alpha ^2} + 4{v^2}\beta  - {v^2}{\beta ^2} + 4{v^2}\alpha \gamma  + 8uv{\alpha ^2}\gamma  - 2{v^2}\alpha \beta \gamma  + 3{v^2}{\alpha ^2}{\gamma ^2}}}\]
\[z =  - \frac{{4v(v + \alpha )( - 2 + \beta  + \alpha \gamma )}}{{8v\alpha  + 4{\alpha ^2} + 4{u^2}{\alpha ^2} + 4{v^2}\beta  - {v^2}{\beta ^2} + 4{v^2}\alpha \gamma  + 8uv{\alpha ^2}\gamma  - 2{v^2}\alpha \beta \gamma  + 3{v^2}{\alpha ^2}{\gamma ^2}}}\]


给定单叶双曲面上的三个点: $ A\left( 1,0,0 \right),B\left( 0,1,0 \right),C\left( \frac{5}{3},0,\frac{4}{3} \right) $
可以给出这个三角形曲面片的表示:
\[x =  - \frac{{ - 16 + 16{u^2} - 16v + 32uv + 11{v^2}}}{{16 + 16{u^2} + 16v + 32uv + 19{v^2}}}\]
\[y = \frac{{16(2 + v)(u + v)}}{{16 + 16{u^2} + 16v + 32uv + 19{v^2}}}\]
\[z =  - \frac{{4v(2 + v)}}{{16 + 16{u^2} + 16v + 32uv + 19{v^2}}}\]

参数 $0 \le u \le 1$,  $ \frac{1}{2}(3 - 4u) - \frac{\sqrt {27 - 40u + 16u^2} }{2\sqrt 3 } \le v \le 0 $



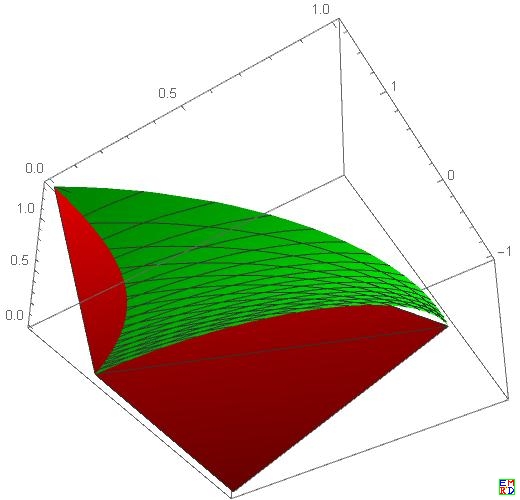
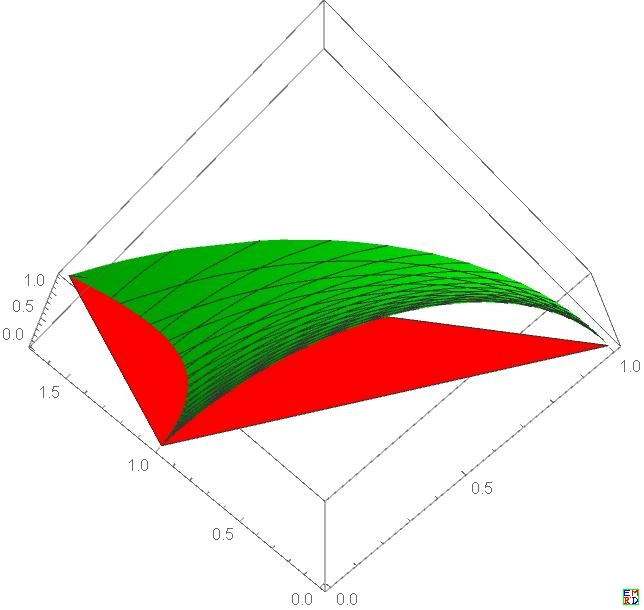
控制点取的$(-1,0,0)$, 即曲面与 $DAB$, $DAC$, $DBC$ 的平面所截部分。

Show[ListPlot3D[{{1,0,0},{0,1,0},{5/3,0,4/3},{-1,0,0}},Mesh->All,PlotStyle->{Red}],ParametricPlot3D[{-((-16+16 u^2-16 v+32 u v+11 v^2)/(16+16 u^2+16 v+32 u v+19 v^2)),(16 (2+v) (u+v))/(16+16 u^2+16 v+32 u v+19 v^2),-((4 v (2+v))/(16+16 u^2+16 v+32 u v+19 v^2))},{u,0,1},{v,1/2 (3-4 u)-Sqrt[27-40 u+16 u^2]/(2 Sqrt[3]),0},PlotStyle->{Green}],AspectRatio->1]

mathematica

问题是你怎么得到的?

ShuXueZhenMiHu

请问为什么需要α，β 和 γ，不是已经有u, v, w 了吗？

葡萄糖

我也相当好奇这个参数怎么来的？另外，希腊字母所代表的参数有什么作用？

wayne

随便一个多项式曲面，换成球坐标系表达，然后把三角函数 都换成 多形式方程，于是 就成了多项式方程组， 接下来的工作就是消元了。
消元的时候 是可以选择合适的GroebnerBasis ，产生新的参数，简化表达式，所以表达形式可以有上千种。
所以，关键的地方 我们如何选择合适的参数，使得参数的几何意义非常显著，做到了这点 那就功德无量了

mathematica

公式太丑了，没有对称性！

creasson

这是计算机辅助几何设计(CAGD)中二次曲面的一个经典问题：一个物体的表面，可通过三角形剖分进行建模，对于剖分的小三角形，希望寻找一个光滑的低次曲面来近似原表面，并要求曲面在截面的边界有一阶连续(法向量方向一致).
如果曲面有参数表示，那么绘图会方便些，这是为什么寻求简单参数表示的原因。