- 注册时间
- 2009-3-10
- 最后登录
- 1970-1-1
- 威望
- 星
- 金币
- 枚
- 贡献
- 分
- 经验
- 点
- 鲜花
- 朵
- 魅力
- 点
- 上传
- 次
- 下载
- 次
- 积分
- 2361
- 在线时间
- 小时
|
 发表于 2022-1-16 20:58:56
|
显示全部楼层
发表于 2022-1-16 20:58:56
|
显示全部楼层
- \!\(\*OverscriptBox["a", "_"]\) = 1/a;
- \!\(\*OverscriptBox["b", "_"]\) = 1/b;
- \!\(\*OverscriptBox["c", "_"]\) = 1/c;(*原点在外心上,并且是单位圆*)
- Chuizu[a_, b_, p_] := (
- \!\(\*OverscriptBox["a", "_"]\) b - a
- \!\(\*OverscriptBox["b", "_"]\) + p (
- \!\(\*OverscriptBox["a", "_"]\) -
- \!\(\*OverscriptBox["b", "_"]\)) +
- \!\(\*OverscriptBox["p", "_"]\) (a - b))/(2 (
- \!\(\*OverscriptBox["a", "_"]\) -
- \!\(\*OverscriptBox["b", "_"]\)));(*=(1/2)[p+(
- \!\(\*OverscriptBox["a", "_"]\)b-a
- \!\(\*OverscriptBox["b", "_"]\)+
- \!\(\*OverscriptBox["p", "_"]\)(a-b))/(
- \!\(\*OverscriptBox["a", "_"]\)-
- \!\(\*OverscriptBox["b", "_"]\))]P到直线AB的垂足*)
- \!\(\*OverscriptBox["Chuizu", "_"]\)[a_, b_, p_] := (a
- \!\(\*OverscriptBox["b", "_"]\) -
- \!\(\*OverscriptBox["a", "_"]\) b +
- \!\(\*OverscriptBox["p", "_"]\) (a - b) + p (
- \!\(\*OverscriptBox["a", "_"]\) -
- \!\(\*OverscriptBox["b", "_"]\)))/(2 (a - b));
- d = Chuizu[c, b, p];
- \!\(\*OverscriptBox["d", "_"]\) =
- \!\(\*OverscriptBox["Chuizu", "_"]\)[c, b, p]; e = Chuizu[a, c, p];
- \!\(\*OverscriptBox["e", "_"]\) =
- \!\(\*OverscriptBox["Chuizu", "_"]\)[a, c, p]; f = Chuizu[a, b, p];
- \!\(\*OverscriptBox["f", "_"]\) =
- \!\(\*OverscriptBox["Chuizu", "_"]\)[a, b, p];
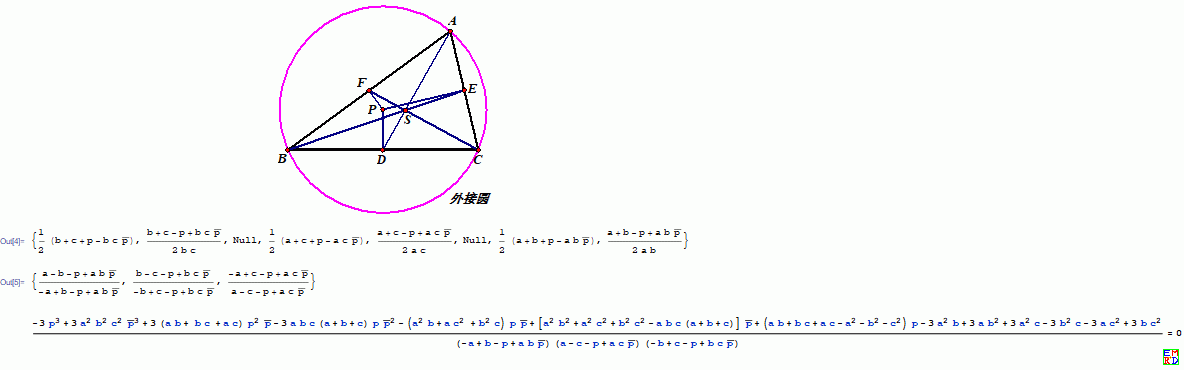
- Simplify[{d,
- \!\(\*OverscriptBox["d", "_"]\), , e,
- \!\(\*OverscriptBox["e", "_"]\), , f,
- \!\(\*OverscriptBox[
- RowBox[{"f", "\[IndentingNewLine]"}], "_"]\)}]
- Simplify[{(a - f)/(b - f), (b - d)/(c - d), (c - e)/(a - e)}]
- Simplify[{(a - f)/(b - f) + (b - d)/(c - d) + (c - e)/(
- a - e)}](*根据Ceva定理,和等于0*)
- Factor[{(a - f)/(b - f) + (b - d)/(c - d) + (c - e)/(a - e)}]
达布曲线是三次方程。 |
-
达布三次曲线
|