欧拉线有关的共线

dlsh

三角形ABC，BC处关于(O)的切线交于D，AE垂直于Euler line且交(O)于另一点E,DE交(O)于另一点F.
设D关于BC的对称点位D'.证明：AD'F共线.
转自纯几何吧

TSC999

非常适合用复平面解析几何方法做此题。

dlsh

1. 
   
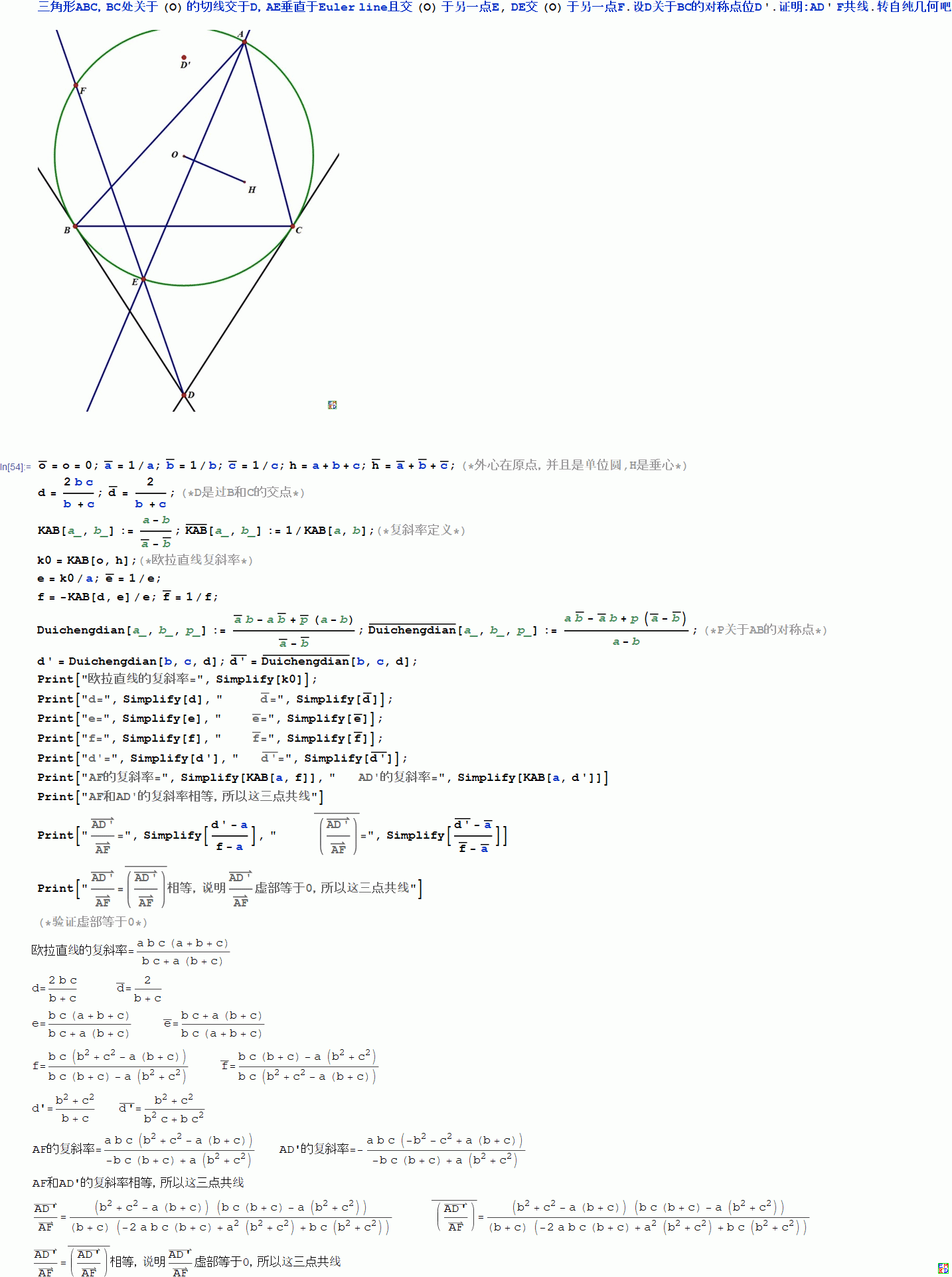
2. \!\(\*OverscriptBox["o", "_"]\) = o = 0;
   
3. \!\(\*OverscriptBox["a", "_"]\) = 1/a;
   
4. \!\(\*OverscriptBox["b", "_"]\) = 1/b;
   
5. \!\(\*OverscriptBox["c", "_"]\) = 1/c; h = a + b + c;
   
6. \!\(\*OverscriptBox["h", "_"]\) =
   
7. \!\(\*OverscriptBox["a", "_"]\) +
   
8. \!\(\*OverscriptBox["b", "_"]\) +
   
9. \!\(\*OverscriptBox["c", "_"]\);(*外心在原点，并且是单位圆,H是垂心*)
   
10. d = (2 b c)/(b + c);
    
11. \!\(\*OverscriptBox["d", "_"]\) = 2/(b + c);(*D是过B和C的交点*)
    
12. KAB[a_, b_] := (a - b)/(
    
13. \!\(\*OverscriptBox["a", "_"]\) -
    
14. \!\(\*OverscriptBox["b", "_"]\));
    
15. \!\(\*OverscriptBox["KAB", "_"]\)[a_, b_] := 1/KAB[a, b];(*复斜率定义*)
    
16. k0 = KAB[o, h];(*欧拉直线复斜率*)
    
17. e = k0/a;
    
18. \!\(\*OverscriptBox["e", "_"]\) = 1/e;
    
19. f = -KAB[d, e]/e;
    
20. \!\(\*OverscriptBox["f", "_"]\) = 1/f;
    
21. Duichengdian[a_, b_, p_] := (
    
22. \!\(\*OverscriptBox["a", "_"]\) b - a
    
23. \!\(\*OverscriptBox["b", "_"]\) +
    
24. \!\(\*OverscriptBox["p", "_"]\) (a - b))/(
    
25. \!\(\*OverscriptBox["a", "_"]\) -
    
26. \!\(\*OverscriptBox["b", "_"]\));
    
27. \!\(\*OverscriptBox["Duichengdian", "_"]\)[a_, b_, p_] := (a
    
28. \!\(\*OverscriptBox["b", "_"]\) -
    
29. \!\(\*OverscriptBox["a", "_"]\) b + p (
    
30. \!\(\*OverscriptBox["a", "_"]\) -
    
31. \!\(\*OverscriptBox["b", "_"]\)))/(a - b);(*P关于AB的对称点*)
    
32. d' = Duichengdian[b, c, d];
    
33. \!\(\*OverscriptBox[
    
34. RowBox[{"d", "'"}], "_"]\) =
    
35. \!\(\*OverscriptBox["Duichengdian", "_"]\)[b, c, d];
    
36. Print["欧拉直线的复斜率=", Simplify[k0]];
    
37. Print["d=", Simplify[d], "     \!\(\*OverscriptBox["d", "_"]\)=",
    
38.   Simplify[
    
39. \!\(\*OverscriptBox["d", "_"]\)]];
    
40. Print["e=", Simplify[e], "    \!\(\*OverscriptBox["e", "_"]\)=",
    
41.   Simplify[
    
42. \!\(\*OverscriptBox["e", "_"]\)]];
    
43. Print["f=", Simplify[f], "    \!\(\*OverscriptBox["f", "_"]\)=",
    
44.   Simplify[
    
45. \!\(\*OverscriptBox["f", "_"]\)]];
    
46. Print["d'=", Simplify[d'], "   \!\(\*OverscriptBox[
    
47. RowBox[{"d", "'"}], "_"]\)=", Simplify[
    
48. \!\(\*OverscriptBox[
    
49. RowBox[{"d", "'"}], "_"]\)]];
    
50. Print["AF的复斜率=", Simplify[KAB[a, f]], "   AD'的复斜率=",
    
51. Simplify[KAB[a, d']]]
    
52. Print["AF和AD'的复斜率相等，所以这三点共线"]
    
53. Print["\!\(\*FractionBox[OverscriptBox[
    
54. RowBox[{"AD", "'"}], "\[RightVector]"], OverscriptBox["AF", \
    
55. "\[RightVector]"]]\)=", Simplify[(d' - a)/(f - a)],
    
56.   "     \!\(\*OverscriptBox[
    
57. RowBox[{" ",
    
58. RowBox[{"(", FractionBox[OverscriptBox[
    
59. RowBox[{"AD", "'"}], "\[RightVector]"], OverscriptBox["AF", \
    
60. "\[RightVector]"]], ")"}]}], "_"]\)=", Simplify[(
    
61. \!\(\*OverscriptBox[
    
62. RowBox[{"d", "'"}], "_"]\) -
    
63. \!\(\*OverscriptBox["a", "_"]\))/(
    
64. \!\(\*OverscriptBox["f", "_"]\) -
    
65. \!\(\*OverscriptBox["a", "_"]\))]]
    
66. Print["\!\(\*FractionBox[OverscriptBox[
    
67. RowBox[{"AD", "'"}], "\[RightVector]"], OverscriptBox["AF", \
    
68. "\[RightVector]"]]\)=\!\(\*OverscriptBox[
    
69. RowBox[{"(", FractionBox[OverscriptBox[
    
70. RowBox[{"AD", "'"}], "\[RightVector]"], OverscriptBox["AF", \
    
71. "\[RightVector]"]], ")"}], \
    
72. "_"]\)相等，说明\!\(\*FractionBox[OverscriptBox[
    
73. RowBox[{"AD", "'"}], "\[RightVector]"], OverscriptBox["AF", \
    
74. "\[RightVector]"]]\)虚部等于0，所以这三点共线"](*验证虚部等于0*)

复制代码