- 注册时间
- 2009-3-10
- 最后登录
- 1970-1-1
- 威望
- 星
- 金币
- 枚
- 贡献
- 分
- 经验
- 点
- 鲜花
- 朵
- 魅力
- 点
- 上传
- 次
- 下载
- 次
- 积分
- 2361
- 在线时间
- 小时
|
 发表于 2022-9-1 21:40:12
|
显示全部楼层
发表于 2022-9-1 21:40:12
|
显示全部楼层
- Clear["Global`*"]
- \!\(\*OverscriptBox["a", "_"]\) = 1/a;
- \!\(\*OverscriptBox["b", "_"]\) = 1/b;
- \!\(\*OverscriptBox["c", "_"]\) = 1/c;
- Midpoint[a_, b_] := (a + b)/2;
- \!\(\*OverscriptBox["Midpoint", "_"]\)[a_, b_] := (
- \!\(\*OverscriptBox["a", "_"]\) +
- \!\(\*OverscriptBox["b", "_"]\))/2;(*中点公式*)
- kAB[a_, b_] := (a - b)/(
- \!\(\*OverscriptBox["a", "_"]\) -
- \!\(\*OverscriptBox["b", "_"]\));
- \!\(\*OverscriptBox["kAB", "_"]\)[a_, b_] := 1/kAB[a, b];(*复斜率定义*)
- kAB[a_, b_, c_] := kAB[a, b]/kAB[b, c];(*e^(2iB) 等于复斜率相除*)
- \!\(\*OverscriptBox["Jd", "_"]\)[k1_, a1_, k2_, a2_] := -((a1 - k1
- \!\(\*OverscriptBox["a1", "_"]\) - (a2 - k2
- \!\(\*OverscriptBox["a2", "_"]\)))/(
- k1 - k2));(*复斜率等于k1,过点A1与复斜率等于k2,过点A2的直线交点*)
- Jd[k1_, a1_, k2_, a2_] := -((k2 (a1 - k1
- \!\(\*OverscriptBox["a1", "_"]\)) - k1 (a2 - k2
- \!\(\*OverscriptBox["a2", "_"]\)))/(k1 - k2));
- FourPoint[a_, b_, c_, d_] := ((
- \!\(\*OverscriptBox["c", "_"]\) d - c
- \!\(\*OverscriptBox["d", "_"]\)) (a - b) - (
- \!\(\*OverscriptBox["a", "_"]\) b - a
- \!\(\*OverscriptBox["b", "_"]\)) (c - d))/((a - b) (
- \!\(\*OverscriptBox["c", "_"]\) -
- \!\(\*OverscriptBox["d", "_"]\)) - (
- \!\(\*OverscriptBox["a", "_"]\) -
- \!\(\*OverscriptBox["b", "_"]\)) (c - d));(*过两点A和B、C和D的交点*)
- \!\(\*OverscriptBox["FourPoint", "_"]\)[a_, b_, c_, d_] := -(((c
- \!\(\*OverscriptBox["d", "_"]\) -
- \!\(\*OverscriptBox["c", "_"]\) d) (
- \!\(\*OverscriptBox["a", "_"]\) -
- \!\(\*OverscriptBox["b", "_"]\)) - ( a
- \!\(\*OverscriptBox["b", "_"]\) -
- \!\(\*OverscriptBox["a", "_"]\) b) (
- \!\(\*OverscriptBox["c", "_"]\) -
- \!\(\*OverscriptBox["d", "_"]\)))/((a - b) (
- \!\(\*OverscriptBox["c", "_"]\) -
- \!\(\*OverscriptBox["d", "_"]\)) - (
- \!\(\*OverscriptBox["a", "_"]\) -
- \!\(\*OverscriptBox["b", "_"]\)) (c - d)));
- e = Midpoint[c, b];
- \!\(\*OverscriptBox["e", "_"]\) =
- \!\(\*OverscriptBox["Midpoint", "_"]\)[c, b]; d = Midpoint[c, a];
- \!\(\*OverscriptBox["d", "_"]\) =
- \!\(\*OverscriptBox["Midpoint", "_"]\)[c, a]; f = Midpoint[b, a];
- \!\(\*OverscriptBox["f", "_"]\) =
- \!\(\*OverscriptBox["Midpoint", "_"]\)[b, a];
- d0 = Jd[a c, d, kAB[c, f], c];
- \!\(\*OverscriptBox["d0", "_"]\) =
- \!\(\*OverscriptBox["Jd", "_"]\)[a c, d, kAB[c, f], c]; e0 =
- Jd[b c, e, kAB[c, f], c];
- \!\(\*OverscriptBox["e0", "_"]\) =
- \!\(\*OverscriptBox["Jd", "_"]\)[b c, e, kAB[c, f],
- c];(*d0和e0代替d和e,防止死循环*)
- k = FourPoint[b, e0, d0, a];
- \!\(\*OverscriptBox["k", "_"]\) =
- \!\(\*OverscriptBox["FourPoint", "_"]\)[b, e0, d0, a];
- Simplify[{1, d0,
- \!\(\*OverscriptBox["d0", "_"]\), e0,
- \!\(\*OverscriptBox["e0", "_"]\), k,
- \!\(\*OverscriptBox["k", "_"]\)}]
- Simplify[{2, kAB[c, k], kAB[c, f]}]
- Simplify[{3, kAB[c, k]/(-a c), -a b/kAB[c, f], ,
- kAB[k, c, f]}](*AC和AB的复斜率是-ac,-ab,验证\[Angle]ACK=\[Angle]BCF*)
- Simplify[{4, kAB[a, k, b], b/a}](*验证\[Angle]AKB=2C*)
第三行结果说明相等条件需要解二次方程,而不是四次。
从计算结果看,还有更深刻的几何意义。 |
-
好看的结果
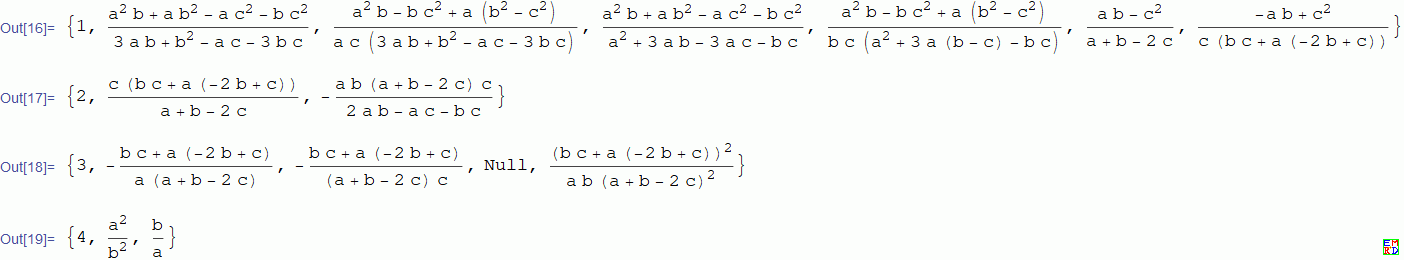
|