圆锥曲线上的四点共圆

hujunhua

mathe 发表于 2022-12-24 12:47
不诡异，两个圆它们有两个公共虚圆点在无穷远直线上。
这个问题再一般化就是如果三条圆锥曲线有两个公共点 ...

回到圆的根轴，显得忽上忽下的。
寻求一个纯射影的证明，我已经不会了。
我找到一个用三次曲线交点定理的证明。
两条三次曲线一般有九个交点，经过其中8点的第三条三次曲线必过第9点。

mathe

两条有理系数圆锥曲线如果有3个交点为有理点，则第4个交点也是有理点。
因为可以联立消去$y^2$后得到$y=frac{ax^2+bx+c}{dx+e)$代回任意一个方程得到一个关于 `x` 的 4 次有理系数方程.
已知 3 个根是有理数，根据韦达定理马上得出第 4 个根也是有理数。

推论：一个圆与一条有理系数圆锥曲线交于 3 个有理点，则第 4 个交点也是有理点。
因为，过 3 个有理点的圆方程显然也都是有理系数。

联想到由椭圆曲线与直线的关系所定义的椭圆曲线上的一种“加法”及有理点群，我们也许能够类似地定义二次曲线上的一种“加法”并构成有理点群。
如果给定的二次曲线上四点`A,B,C,D`共圆，我们希望所定义的加法"`+`"使得 `A+B+C+D=O`.
由于所有已知加法表达式都是四个点相加为0，一个合法定义的零元` O `应满足` 4O=0 `。

现在以椭圆为例子，我们试着定义其上点列的一个“加法”运算。
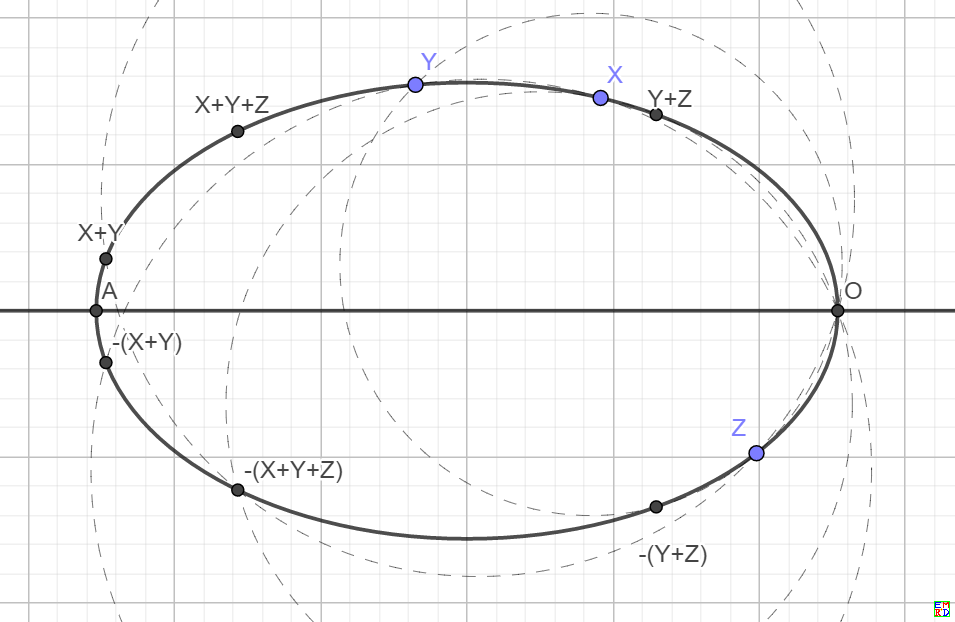
1、定义椭圆右顶点为加法零元`O`。（满足4O=0的点只能是椭圆长短轴四个端点）
2、考虑与`O`相切的圆，对于椭圆上任意一个点`X`, 定义其关于横轴的镜像点为`-X`.
     注意，椭圆的左顶点`A`不是零元，但是`A=-A`，或者说`A+A=O`, 即`A`是一个 2 阶点.
3、对于椭圆上 3 个点`X,Y,Z`, 如果`O,X,Y,Z` 4点共圆，那么`X+Y+Z=O`.
     显然，这样定义的"加法"满足交换律，下图显示也满足结合律。
     于是，按上面的“推论”，椭圆上所有有理点构成一个加法群。

考虑到2#椭圆上4点共圆的判别式可以写作 `θ_1+θ_2+θ_3+θ_4\equiv0\pmod{2\pi}`，以上选择左顶点为零元所定义的加法正与此同构。

ellpise.ggb (44.43 KB, 下载次数: 0)

2023-1-1 09:53 上传

点击文件名下载附件

mathe

如上图，如果我们在椭圆上任意选择点X,然后按上面定义做出2X,3X,...,7X,...
然后依次做O,X,2X,3X,...处切线，相邻点的切线依次交于图中绿色点。可以看出这些绿色点也会落在同一个椭圆上。
所以这个正好和轨迹是否为圆 中二次对合匹配。
这个意味中椭圆中，离心角成等差数列的点中，相邻点切线交点落在同一个椭圆上（和原椭圆同中心同对称轴）

hujunhua

对于抛物线，顶点是零元的唯一选择。
所定义的加法与3#的`x_1+x_2+x_3+x_4=0`同构。
至于3#的结论是在`x_i\ne x_j`的前提下得出来的，并不妨碍存在切点的情况，按极限理解就行。

双曲线，也能定义的与5#和8#的判别式同构。

lsr314

圆锥曲线上A, B, C, D四点共圆，记4个内角的平分线为a, b, c, d.
则四线形abcd的对角线正是圆锥曲线的两个主轴方向。

mathe

lsr314 发表于 2023-1-4 13:25
圆锥曲线上A, B, C, D四点共圆，记4个内角的平分线为a, b, c, d.
则四线形abcd的对角线正是圆锥曲线的两主轴方向.

这个结论挺有意思，趣题有妙解。
让椭圆的两主轴方向为坐标轴方向，记椭圆和圆的方程为`f(x,y)=0`和`g(x,y)=0`, 则两者都不含`xy`项。
于是经过`A, B, C, D`的所有二次曲线`f+λg=0`也都不包含`xy`项，所以它们的主轴也都在坐标轴方向。
考虑上述二次曲线系中的三条退化曲线（包括直线AB和CD、直线AC和BD，直线BC和AD），它们的角平分线正好是坐标轴方向。
记直线AB和CD的交点为E，即∠BEC的平分线平行坐标轴。
而 a 和 d 的交点为△AED的旁心，b 和 c 的交点为△BCE的内心，都在∠BEC的平分线上，
所以这两个"心"的连线就是∠BEC的平分线，为坐标轴方向之一。

hujunhua

于是我们终于得到了二次曲线上四点共圆的几何判据：
二次曲线上四点共圆，当且仅当一对对边的夹角平分线为二次曲线主轴方向。