轨迹是否为圆

mathe · 发表于 2011-1-23 08:21:37

马上注册，结交更多好友，享用更多功能，让你轻松玩转社区。

您需要登录才可以下载或查看，没有账号？欢迎注册

×

假设$1<t<k$,其中$t$, $k$都是正整数
平面上两个圆$O_1$, $O_2$, 其中圆$O_1$在圆$O_2$内部。
过圆$O_2$上一个动点$P_1$向圆$O_1$一个固定方向（顺时针或者逆时针方向）做一条切线切$O_1$于$T_1$,交$O_2$于另外一个点$P_2$,
同样过$P_2$向圆$O_1$做另外一条切线切$O_1$于$T_2$,交$O_2$于另外一个点$P_3$,
...
直到得到$T_k$
直线$T_1T_t$和$T_{k-t+1}T_k$交于一点$Q$
证明或否定$Q$点轨迹是一个圆，并且这个圆和圆$O_1$, 圆$O_2$有公共的极点极线对。也就是说存在平面上一个点$H$, $H$向三个圆做切线的6个切点共线（特别的，对于同心圆，认为$H$在无穷远）

推广一下到普通二次曲线，同样有类似猜想，而这时需要另外证明三条二次曲线交于公共四个点（包含虚点或重合点(相切情况算两个重合的点)）

最后链接 https://bbs.emath.ac.cn/thread-5485-1-1.html 中可以通过椭圆曲线解决这里的问题

wayne · 发表于 2011-1-23 15:24:51

用解析几何有点麻烦，

我高等几何还没看完呢

mathe · 发表于 2011-1-24 09:18:58

今天用几何画板作图检验了一下，对于一般的情况不成立，但是好像对于$t=k-1$成立。
而对于一般情况好像结果是一个普通的二次曲线，而不一定是圆。但是这个二次曲线同样和两个原先的圆拥有统一的极点和极线。

mathe · 发表于 2011-1-25 14:02:26

思考这个问题得出一个有意思的变换。
设$C_1$, $C_2$是平面上的两条圆锥曲线. $C_1$（上的点列）是$C_2$作用对象，$C_2$是变换曲线。
自$C_2$上的动点$Q$引$C_1$的两条切线得切点$P$和$R$，那么$P\rightarrow R$就确定了$C_1$上点列的一个变换，且称之为$C_1$关于$C_2$的一个圆锥变换或二次对合变换（不知道数学上是否已经有这个变换的定义，需要注意的是二次对合变换不是对合变换）。

为简化计算，我们将曲线$C_1$射影成抛物线$y=x^2$，使得$C_1$上的点$(x,y)$可以写成参数形式$(x,x^2)$。
假定上述各点坐标为$Q(x_0,y_0),P(x_1,y_1),R(x_2,y_2)$.
$PR$是$Q$关于$C_1$的极线，其直线方程为$2x_0x-y-y_0=0$
$PR$和$C_1$交于$(x_1,y_1),(x_2,y_2)$两点，也就是方程
$x^2-2x_0x+y_0=0$的两根是$x_1,x_2$
由韦达定理可得$x_1+x_2=2x_0,x_1x_2=y_0$
由此可见,  若圆锥变换$C_2$将 $C_1$上的点$(x_1,y_1)$变换为$(x_2,y_2)$, 那么$(\frac{x_1+x_2}2,x_1x_2)$将满足曲线$C_2$的方程。
反之可得，曲线$C_1:y=x^2$上点列的一个变换为圆锥变换的充要条件是$(u,v)=(\frac{x_1+x_2}2,x_1x_2)$满足一条圆锥曲线方程。

现在，我们设$C_2$的方程为$4A x^2+2B x y+C y^2+2D x+E y+F=0$,
将$(\frac{x_1+x_2}2,x_1x_2)$代入方程得
$A(x_1+x_2)^2+B(x_1+x_2)x_1x_2+C(x_1x_2)^2+D(x_1+x_2)+E(x_1x_2)+F=0$  (1)
我们发现可以将上面方程改成矩阵形式
$[x_1,x_1^2,1][(2A+E,B,D),(B,C,A),(D,A,F)][(x_2),(x_2^2),(1)]=0$  (2)
可以看到，对于源$(x_1,x_1^2)$,  像$(x_2,x_2^2)$一般有两解，且记为$x_{2_1},x_{2_2}$.
假定$x_1\rightarrow x_{2_1}$是沿顺时针方向的，那么$x_1\rightarrow x_{2_2}$就是沿逆时针方向的。任取一个方向，就得到一个圆锥变换。
也即是说，任意一个实对称矩阵确定圆锥曲线上一对互逆的圆锥变换。

设(2)的展开式为$u x_2^2+v x_2+w=0$, 易知这里$u,v,w$都是$x_1,x_1^2,1$的线性组合
所以若将$\frac{x_{2_1}+x_{2_2}}2=-v/2u,x_{2_1}x_{2_2}=w/u$看成一个平面上点的坐标，那么它正好是点$(x_1,x_1^2,1)$的一个射影变换，
由于动点$(x_1,x_1^2,1)$满足圆锥曲线$y=x^2$的方程，故$(\frac{x_{2_1}+x_{2_2}}2,x_{2_1}x_{2_2})$也满足一条圆锥曲线的方程
也就是说, 变换 $x_{2_1}\rightarrow x_{2_2}$也是$C_1$上点列的一个圆锥变换。
而 $x_{2_1}\rightarrow x_{2_2}$是 $x_{2_1}\rightarrow x_1$ 和$x_1\rightarrow x_{2_2}$的复合，故得圆锥变换的平方还是圆锥变换。
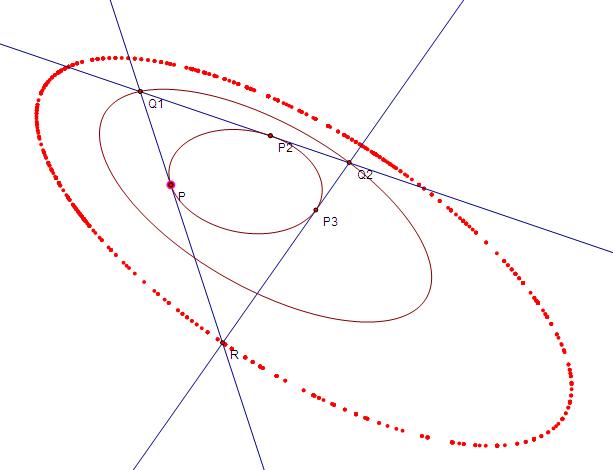
其几何意义就是给定圆锥曲线$C_1,C_2$,从$C_1$上任意一动点P出发向某个方向(顺时针方向vs逆时针方向)作$C_1$切线交$C_2$于$Q_1$,过$Q_1$作$C_1$的另一条切线切$C_1$于$P_2$交$C_2$于$Q_2$,过$Q_2$做$C_1$的另一条切线切$C_1$于$P_3$,那么$PQ_1$和$Q_2P_3$的交点的轨迹是圆锥曲线.

mathe · 发表于 2011-1-25 16:59:50

几何画板作图表明同一个圆锥变换的任意次方还是圆锥变换，不过不知道如何证明，当然两个不同的圆锥变换的复合不一定是圆锥变换

mathe · 发表于 2011-1-25 20:48:08

对于(2)中矩阵我们可以看成二次曲线$C_3$:
$(x,y,z)\begin{bmatrix}2A+E&B&D\\B&C&A\\D&A&F\end{bmatrix} \begin{bmatrix}x\\y\\z\end{bmatrix}=0$
于是(2)式的几何意义就是$(x_2,x_2^2,1)$在点$(x_1,x_1^2,1)$关于$C_3$的极线上（也就是关于$C_3$的极线和$C_1$的交点)

mathe · 发表于 2011-1-28 17:26:17

4#的图中离散点列$P,P2,P3,...$是一个圆锥变换迭代点列，$Q_1,Q_2,...$也是。
对于圆锥曲线$C_1$上的一个圆锥变换$C_2$迭代点列$\{P_i\}$，它在一个射影变换$M$作用下的映像$\{M(P_i)\}$是圆锥曲线$M(C_1)$上的圆锥变换$M(C_2)$迭代点列。

通过射影对应，我们可以定义直线上的圆锥变换迭代点列。
如果$P_1,P_2,P_3,....,P_n,...$是圆锥曲线$C$上一个圆锥变换迭代点列，在 $C$上任意选择一点$P$,连接$PP_1,PP_2,...,PP_n,..$.等分别交直线 $l$ 到$Q_1,Q_2,Q_3,...,Q_n,...$,那么我们称$Q_1,Q_2,Q_3,...,Q_n,...$为直线 $l$ 上的圆锥变换迭代点列。
在另外圆锥曲线$C'$上任取一点$P'$,分别连接$Q_1,Q_2,...,Q_n,...$到$P'$的直线交圆锥曲线$C'$得出的交点序列还是$C'$上的圆锥变换迭代点列。
同样，两条直线之间点列的投影也保持圆锥变换的性质。

mathe · 发表于 2011-1-28 17:27:33

对圆锥曲线$C$上任取的6个不同点$P_1,P_2,...,P_6$, $C$上恰好存在一个的由此6点引导的圆锥变换迭代点列$P_1,P_2,...,P_6,...$.

mathe · 发表于 2011-1-31 08:40:09

根据前面的知识，我们现在知道对于上面定义的“圆锥变换”或“二次对合变换”，我们可以有下面四种不同的定义:
i)给定圆锥曲线C1,以及另外一个圆锥曲线C2,对于C1上任意一点P1,过P1做C2的任意一条切线交C1于P2,同样过P2做C2的另外一条切线交C1于P3,...依次类推，我们可以得到一个序列P1,P2,P3,...,Pn,...
ii)对偶的，给定圆锥曲线C1,以及另外一个圆锥曲线C2,对于C1上任意一点P1,P1点的C1的切线交于C2于一点，而过着一点可以做C2的另外一条切线，切点为P2,,同样P2的这条切线交C2于另外一点，而过这一点C1的另外一条切线的切点为P3,...依次类推，我们可以得到一个序列P1,P2,P3,...,Pn,...
我们称P1关于这个二次对合变换的像是P2,P2关于这个二次对合变换的像是P3,...而这个序列是对应的一个二次对合变换序列。
iii)给定圆锥曲线C1和C2,对于C1上任意一点P1,P1关于C2的极线和C1的一个交点定义为P2,然后P2关于C2的极线（必然过P1）和C1的另外一个交点为P3,P3关于C2的极线和C1的另外一个交点为P4,....依次类推，我们可以得到一个序列P1,P2,P3,...,Pn,...
我们称P1关于这个二次对合变换的像是P2,P2关于这个二次对合变换的像是P3,...而这个序列是对应的一个二次对合变换序列。
iv)对偶于iii),给定圆锥曲线C1和C2,对于C1上任意一点P1,P1处切线关于C2的极点可以向C1引任意一切线，切点定义为P2,然后P2处切线关于C2的极点向C1做另外一条切线（其中一条必然切于P1)切C1于P3,,....依次类推，我们可以得到一个序列P1,P2,P3,...,Pn,...
我们称P1关于这个二次对合变换的像是P2,P2关于这个二次对合变换的像是P3,...而这个序列是对应的一个二次对合变换序列。
而显然同一个圆锥变换如果选择不同的初始点，可以得到很多不同的二次对合变换序列。

四种定义中的曲线C1我们可以称之为这个二次对合变换的目标曲线，而其中的曲线C2可以分别称为第一(二，三，四）类变换曲线。

mathe · 发表于 2011-1-31 08:58:54

我们现在查看第一类变换曲线，在复数范围，通常情况，它和目标曲线C1有四条公切线。
对于某一条公切线P1Q1,其中切C1于P1,切第一类变换曲线C2于Q1.由于过P1可以做C2的两条切线，其中另外一条为为P1Q2,其中交C1于另外一个点P2.
于是如果我们从P2开始做二次对合变换序列，并将第一次变换的像选择为P1,那么下一次变换，由于切线P1Q1是公切线，下一次变换结果还是P1,而再下一次变换，由于我们需要切换到过P1的另外一条切线(P1Q2),所以又变换到P2,于是我们得到对应的二次对合变换序列为
P2,P1,P1,P2,....

也就是这个变换序列中点P1为连续重复出现一次（所以我们也知道对于每个点，其变换的像同它在序列中的位置也有关系，总共有两种可能的取值）。
另外一方面，如果一个点会在某个变换序列中连续重复出现，那么我们代入4#中(2)式(定义3的代数形式）,得到如果C1通过射影变换成$y=x^2$后，横坐标x必然是一个四次方程的根，所以最多四个解。
而由于通常情况，目标曲线和第一类变换曲线有且仅有四条公切线，这说明这种在某个序列中连续重复出现一次的点有且仅有四个，正好是目标曲线和第一类变换曲线公切线在目标曲线上的切点，我们称这种点为这个二次对合变换的驻点。当然特殊的，如果目标曲线正好和第一类变换曲线在某点相切，那么情况退化为两个驻点重合的情况，而对应的驻点处二次变换序列为常数点序列(P1,P1,P1,...）,这个点可以称为常驻点，显然常驻点最多两个。如果常驻点根据重数看成多个驻点，那么任何二次对合变换正好有且仅有四个驻点。

账号		自动登录	找回密码
密码			欢迎注册

[讨论] 轨迹是否为圆

马上注册，结交更多好友，享用更多功能，让你轻松玩转社区。

相关帖子

评分