- 注册时间
- 2007-12-27
- 最后登录
- 1970-1-1
- 威望
- 星
- 金币
- 枚
- 贡献
- 分
- 经验
- 点
- 鲜花
- 朵
- 魅力
- 点
- 上传
- 次
- 下载
- 次
- 积分
- 49492
- 在线时间
- 小时
|
 发表于 2025-1-4 20:45:53
|
显示全部楼层
发表于 2025-1-4 20:45:53
|
显示全部楼层
由于微分方程为
\(\begin{cases}\frac{d}{dt}h(t)=a_1h(t)-a_2h^2(t)-a_3h(t)s(t)-x\\
\frac{d}{dt}s(t)=b_1s(t)-b_2s^2(t)-b_3h(t)s(t)-y\end{cases}\)
那么对于一个稳态,应该充分长时间后h,s都趋向常数\(h^*,s^*\),
于是必然有等式
\(\begin{cases}x=a_1h^*-a_2h^{*2}-a_3h^*s^*\\
y=b_1s^*-b_2s^{*2}-b_3h^*s^*\end{cases}\)
而我们需要判断对于哪些\(h^*,s^*\)是稳态。
为了保持这个状态是稳态的,那么对于充分接近\((h^*,s^*)\)的\((h,s)\), 根据几何意义,必然有这个点处方向导数和向量\((h-h^*,s-h^*)\)夹角是钝角,也就是
\(\frac{dh}{dt}(h-h^*)+\frac{ds}{dt}(s-s^*)\lt 0\)
代入并且去掉高阶无穷小,我们得到
\((a_1 (h-h^*)-2a_2(h-h^*)h-a_3(h-h^*)s-a_3h(s-s^*))(h-h^*)+(b_1(s-s^*)-2b_2(s-s^*)s-b_3(h-h^*)s-b_3h(s-s^*))(s-h^*)\lt 0\)
也就是
\((a_1 -2a_2h^*-a_3s^*)(h-h^*)^2-(a_3h^*+b_3s^*)(s-s^*)(h-h^*)+(b_1-2b_2s^*-b_3h^*)(s-s^*)^2\lt 0\)
也就是要求矩阵
\(\begin{bmatrix}a_1 -2a_2h^*-a_3s^*&-\frac{a_3h^*+b_3s^*}2\\-\frac{a_3h^*+b_3s^*}2&b_1-2b_2s^*-b_3h^*\end{bmatrix}\)
负定。
所以等价于要求
\(\begin{cases}a_1\lt 2a_2h^*+a_3s^*\\
b_1\lt 2b_2s^*+b_3h^*\\
4(a_1 -2a_2h^*-a_3s^*)(b_1-2b_2s^*-b_3h^*)\gt (a_3h^*+b_3s^*)^2
\end{cases}\)
于是收敛\(h^*,s^*\)分布如图第一象限部分中彩色射线上方和双曲线中间部分
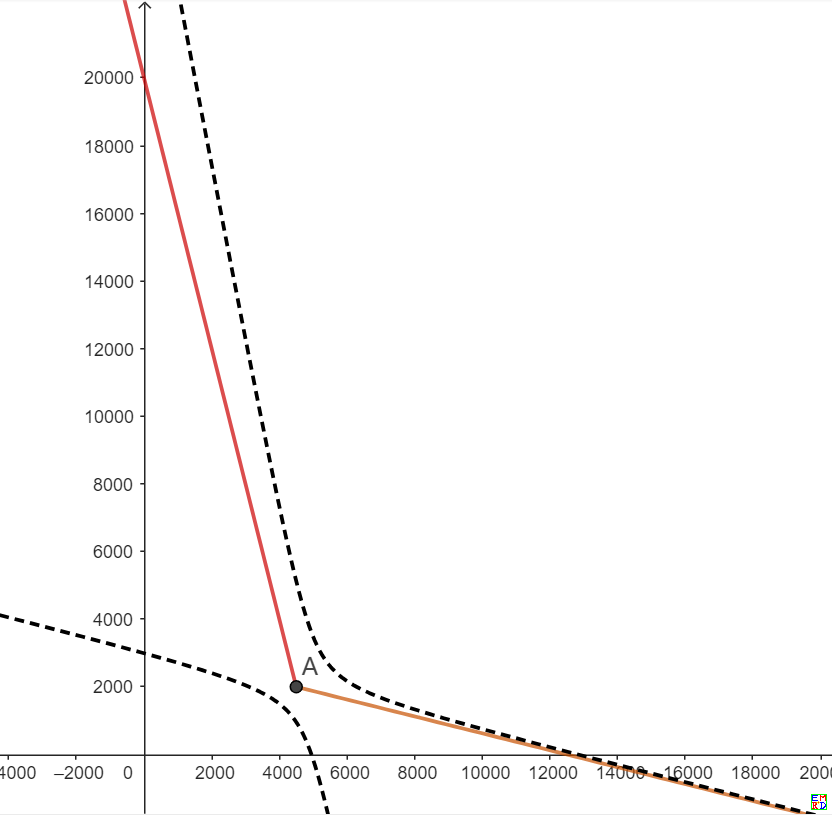
然后回答2/3问题应该不难了。唯一的问题是这里的题目给定了初始分布,给定的初始分布使用固定的砍伐策略不一定能够保证收敛到指定的\((h^*,s^*)\),但是如果允许开始采用变化的砍伐策略,应该能够通过调整树木的分布最终引导到指定的收敛位置。
|
|