- 注册时间
- 2008-11-26
- 最后登录
- 1970-1-1
- 威望
- 星
- 金币
- 枚
- 贡献
- 分
- 经验
- 点
- 鲜花
- 朵
- 魅力
- 点
- 上传
- 次
- 下载
- 次
- 积分
- 149504
- 在线时间
- 小时
|
 发表于 2021-1-18 10:10:25
|
显示全部楼层
发表于 2021-1-18 10:10:25
|
显示全部楼层
本帖最后由 mathematica 于 2021-1-18 10:15 编辑
- Clear["Global`*"];
- (*A点坐标*)
- {xa,ya}={1,Sqrt[3]}
- (*B点坐标,联立方程求B点坐标*)
- {xb,yb}={x,y}/.Flatten@FullSimplify@Solve[x^2/2+y^2/6==1&&(y-ya)/(x-xa)==-k,{x,y}]
- (*C点坐标,联立方程求C点坐标*)
- {xc,yc}={x,y}/.Flatten@FullSimplify@Solve[x^2/2+y^2/6==1&&(y-ya)/(x-xa)==k,{x,y}]
- (*计算BC点的斜率,似乎是常数*)
- kBC=((yb-yc)/(xb-xc))//FullSimplify
- (*计算三角形的面积,此处应该取绝对值,但是最大最小值都求解了就可以了*)
- ff=FullSimplify[Det[{{xa,ya,1},{xb,yb,1},{xc,yc,1}}]/2]
- (*画图观察是奇函数*)
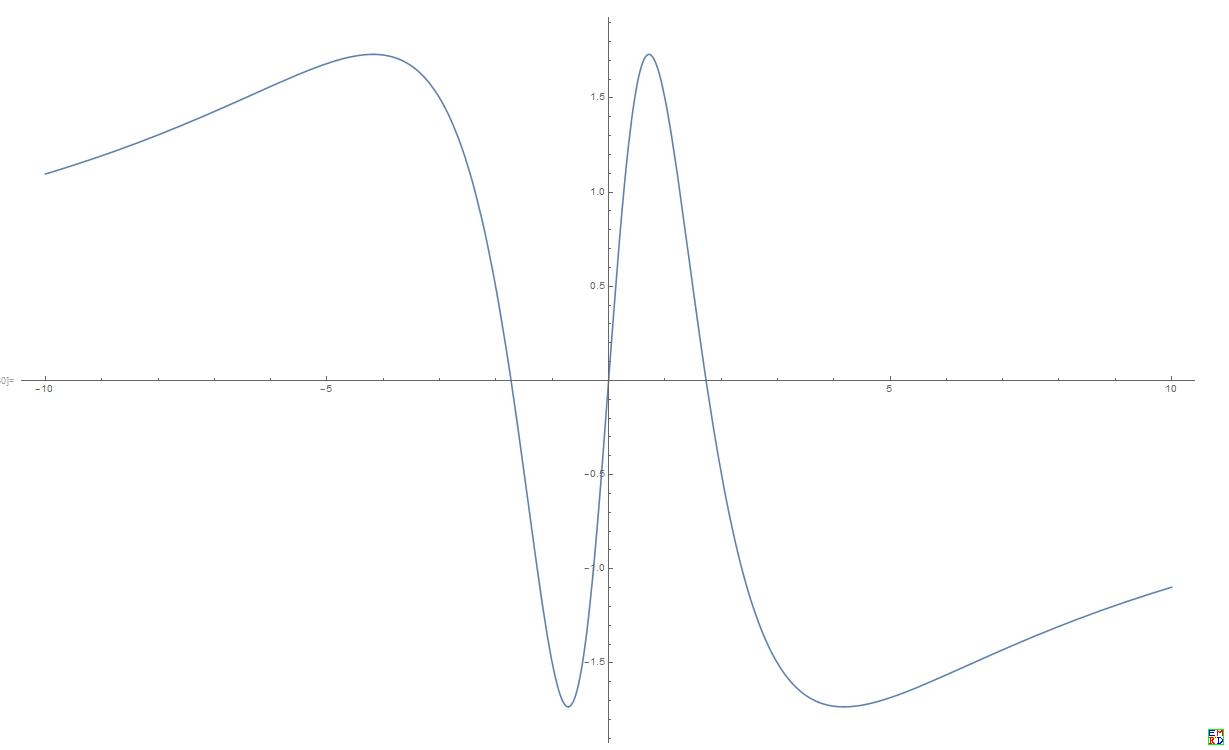
- Plot[ff,{k,-10,10}]
- (*求出所有导数等于零的点*)
- aaa=FullSimplify@Solve[D[ff,k]==0,{k}]
- (*查看所有最值点大小*)
- bbb=(ff/.aaa)//FullSimplify
计算结果
B点坐标
\[\left\{\frac{2 \left(\sqrt{3} k-3\right)}{k^2+3}+1,\frac{6 \left(k+\sqrt{3}\right)}{k^2+3}-\sqrt{3}\right\}\]
C点坐标
\[\left\{1-\frac{2 \left(\sqrt{3} k+3\right)}{k^2+3},\frac{6 \left(\sqrt{3}-k\right)}{k^2+3}-\sqrt{3}\right\}\]
BC斜率
\[\sqrt{3}\]
面积代数值
\[-\frac{12 k \left(k^2-3\right)}{\left(k^2+3\right)^2}\]
导数等于零的点
\[\left\{\left\{k\to \sqrt{3}-\sqrt{6}\right\},\left\{k\to \sqrt{9-6 \sqrt{2}}\right\},\left\{k\to -\sqrt{3} \left(\sqrt{2}+1\right)\right\},\left\{k\to \sqrt{3}+\sqrt{6}\right\}\right\}\]
极值点大小
\[\left\{-\sqrt{3},\sqrt{3},\sqrt{3},-\sqrt{3}\right\}\]
直线AC的斜率与三角形ABC的面积变化函数关系图(没求绝对值)
|
-
|