内接凸N边形的N边形周长最小值问题

数学星空

对于有外接圆的凸四边形还有关系式:

\(mn=ac+bd\)

\(m_1 m_2=n_1 n_2\)      

\(s=\sqrt{(p-a)(p-b)(p-c)(p-d)},2p=a+b+c+d\)   

若四边形有内切圆时

\(s=\sqrt{abcd}\cos(\frac{A+C}{2})\)

即有内切圆又有外接圆时:

\(s=\sqrt{abcd}\)

则有内接四边形的最小周长

\(L=m_2 \sin(A)+n_1\sin(B)+m_1\sin(C)+n_2\sin(D)=m \sin(A)+n\sin(B)=\frac{m a+m c+n b+n d}{4R}=\frac{S_{ABD}}{a}+\frac{S_{ABC}}{b}+\frac{S_{BCD}}{c}+\frac{S_{ACD}}{d}\)



注: \(t=m_1 m_2=n_1 n_2\) 满足下列方程:

\(-m^4(-n+b+c)(n+b+c)(-c+n+b)(b-c-n)(n+a+d)(-n+a+d)(a-d-n)(-d+n+a)+4m^2(-n+b+c)(n+b+c)(-c+n+b)(b-c-n)(n+a+d)(-n+a+d)(a-d-n)(-d+n+a)t+(a^4-2a^2d^2-2a^2n^2-b^4+2b^2c^2+2b^2n^2-c^4+2c^2n^2+d^4-2d^2n^2)^2t^2=0\)

数学星空

对于\(N=5\)边形



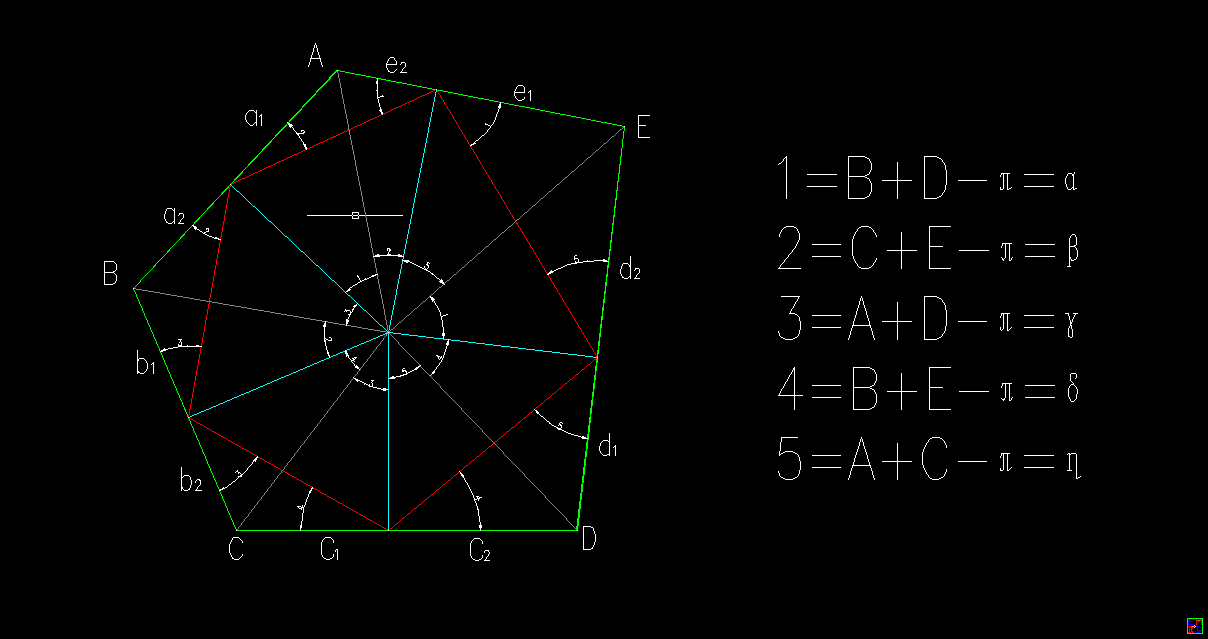
\(\alpha+\beta+A=\pi, \beta+\gamma+B=\pi, \gamma+\delta+C=\pi, \delta+\mu+D=\pi, \mu+\alpha+E=\pi\)

\(\mu=A+C-\pi, \alpha=B+D-\pi, \beta=C+E-\pi, \delta=B+E-\pi, \gamma=A+D-\pi\)


\(\frac{\sin(\alpha)}{\sin(\beta)}=k_1, \frac{\sin(\beta)}{\sin(\gamma)}=k_2, \frac{\sin(\gamma)}{\sin(\delta)}=k_3, \frac{\sin(\delta)}{\sin(\mu)}=k_4, \frac{\sin(\mu)}{\sin(\alpha)}=k_5\)

\(\frac{a_1}{e_2}=k_1, \frac{b_1}{a_2} =k_2, \frac{c_1}{b_2}=k_3, \frac{d_1}{c_2}=k_4, \frac{e_1}{d_2}=k_5\)

\(a_1+a_2=a, b_1+b_2=b, c_1+c_2=c, d_1+d_2=d, e_1+e_2=e\)


\(a_1 =\frac{k_1(ak_2k_3k_4k_5-bk_3k_4k_5+ck_4k_5-dk_5+e)}{k_1k_2k_3k_4k_5+1}\)

\(a_2=\frac{bk_1k_3k_4k_5-ck_1k_4k_5+dk_1k_5-ek_1+a}{k_1k_2k_3k_4k_5+1}\)

\(b_1=\frac{k_2(bk_1k_3k_4k_5-ck_1k_4k_5+dk_1k_5-ek_1+a)}{k_1k_2k_3k_4k_5+1}\)

\(b_2=\frac{-(-ck_1k_2k_4k_5+dk_1k_2k_5-ek_1k_2+ak_2-b)}{k_1k_2k_3k_4k_5+1}\)

\(c_1=\frac{-k_3(-ck_1k_2k_4k_5+dk_1k_2k_5-ek_1k_2+ak_2-b)}{k_1k_2k_3k_4k_5+1}\)

\(c_2=\frac{dk_1k_2k_3k_5-ek_1k_2k_3+ak_2k_3-bk_3+c}{k_1k_2k_3k_4k_5+1}\)

\(d_1=\frac{k_4(dk_1k_2k_3k_5-ek_1k_2k_3+ak_2k_3-bk_3+c)}{k_1k_2k_3k_4k_5+1}\)

\(d_2=-\frac{(-ek_1k_2k_3k_4+ak_2k_3k_4-bk_3k_4+ck_4-d)}{k_1k_2k_3k_4k_5+1}\)

\(e_1=-\frac{k_5(-ek_1k_2k_3k_4+ak_2k_3k_4-bk_3k_4+ck_4-d)}{k_1k_2k_3k_4k_5+1}\)

\(e_2=\frac{ak_2k_3k_4k_5-bk_3k_4k_5+ck_4k_5-dk_5+e}{k_1k_2k_3k_4k_5+1}\)

\(L_1^2=a_1^2+e_2^2-2a_1e_2\cos(A), L_2^2=a_2^2+b_1^2-2a_2b_1\cos(B), L_3^2=b_2^2+c_1^2-2b_2c_1\cos(C), L_4^2=d_1^2+c_2^2-2d_1c_2\cos(D), L_5^2=e_1^2+d_2^2-2e_1d_2\cos(E)\)

\(L=L_1+L_2+L_3+L_4+L_5\)