- 注册时间
- 2016-2-17
- 最后登录
- 1970-1-1
- 威望
- 星
- 金币
- 枚
- 贡献
- 分
- 经验
- 点
- 鲜花
- 朵
- 魅力
- 点
- 上传
- 次
- 下载
- 次
- 积分
- 3496
- 在线时间
- 小时
|
马上注册,结交更多好友,享用更多功能,让你轻松玩转社区。
您需要 登录 才可以下载或查看,没有账号?欢迎注册
×
本帖最后由 lsr314 于 2019-1-13 04:35 编辑
几年前思考过一个问题,最近有了一点进展,但是离完全解决还是有很大差距,直接看问题:
考虑连分数$phi=1/(1+1/(1+1/(1+…)))=(sqrt(5)-1)/2$
如果将每个分子里的1换成0到1之间的随机数会怎么样?即考虑下面这个式子:
$X=x_1/(1+x_2/(1+x_3/(1+…)))$
由于每个$x_i$都在$(0,1)$之间,所以一旦每个$x_i$都确定,上面的式子是收敛到一个0到1之间的实数的。
问题就是:假如每个$x_i$各自独立,且均服从$(0,1)$之间的均匀分布,求变量$X$的概率密度函数$f(x)$以及概率分布函数$F(x)$。
通过推导,可以得到以下结论:
$0<x<=1/2$时,$f(x)=2-c,F(x)=(2-c)x$,其中$c=int_0^1F(t)dt=1-int_0^1 tf(t)dt$.
$1/2<=x<1$时,$F(x)=1-x int_0^(1/x-1)F(t)dt$.
所以,$X$在$(0,1/2)$之间是服从均匀分布的,在$(1/2,1)$之间的分布则复杂很多,实际上,$f(x)$被分成无穷多个区间,这些区间的端点刚好就是$phi$的渐进分数。
我们定义$a_0=0,a_n=1/(1+a_(n-1))(n>0)$,则${a_n}$的前几项刚好就是$0,1,1/2,2/3,3/5,5/8,\cdots$
从左到右,将$(0,phi)$划分为$(a_0,a_2)(a_2,a_4)(a_4,a_6)\cdots$
从右到左,将$(phi,1)$划分为$(a_3,a_1)(a_5,a_3)(a_7,a_5)\cdots$
则在每个上述小区间上,$f(x)$是一致的.
根据奇偶性,分布函数可以写成下面的递推式:
$F_1(x)=(2-c)x,a_0<x<a_2$
$(1-F_(2n)(x))/x=sum_(i=1)^(n-1)int_(a_(2i-2))^(a_(2i))F_(2i-1)(t)dt+int_(a_(2n-2))^(1/x-1)F_(2n-1)(t)dt,a_(2n+1)<x<a_(2n-1)$
$(1-F_(2n+1)(x))/x=c-sum_(i=1)^(n-1)int_(a_(2i+1))^(a_(2i-1))F_(2i)(t)dt-int_(1/x-1)^(a_(2n-1))F_(2n)(t)dt,a_(2n)<x<a_(2n+2)$
通过以上递推式,我们可以写出任意一个区间的$F(x)$,比如
$2/3<x<1$时,$F(x)=F_2(x)=1 - ((2 - c) (1 - x)^2)/(2 x)$
$1/2<x<3/5$时,$F(x)=F_3(x)=((2 - c) (1 - 6 x + 12 x^2 + 2 x^2 log(1/x - 1)))/(4 x)$
$5/8<x<2/3$时,$F(x)=F_4(x)=1 - ((2 - c) (12 - 38 x + 31 x^2 + (2 - 4 x ) log((2 x - 1)/(1 - x))))/(8 x)$
去掉以上四个区间,仅剩下$(3/5,5/8)$之间的分布函数还没有写出来,越接近$phi$分布函数越复杂,$F_5(x)$已经不能用初等函数表示出来了。
得出以上结论后,我还想知道以下几个问题的答案:
(1)能否求出$E(X)=1-c$的值?数值上看,$E(X)≈0.374$
(2)能否求出$f(phi)$以及$F(phi)$?
(3)理论上,当$n->∞$时,以下程序输出的结果是否依概率收敛于$E(X)$?
- b[1] = RandomReal[]; Do[b[i + 1] = RandomReal[]/(1 + b[i]), {i, n}]
- Mean[Table[a[i], {i, n}]]
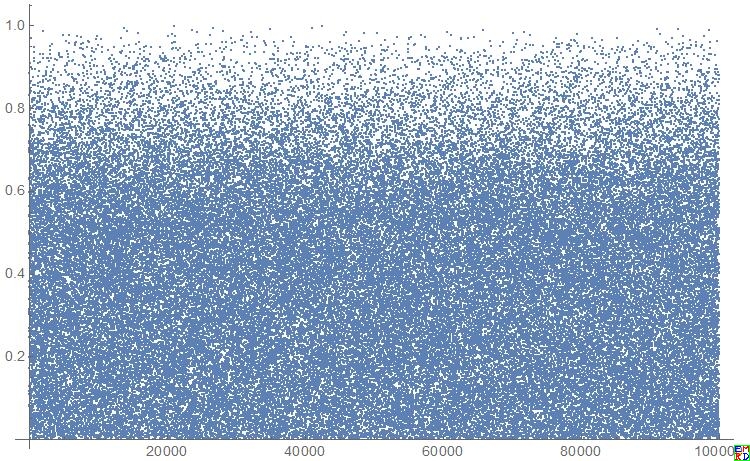
附一张分布图,可以看出在上半部分,点是越来越稀疏的,从$F_2(x)$的导函数也不难看出。
|
-
|