数学研发网设为首页收藏本站
切换到窄版

 找回密码
 欢迎注册
数学研发论坛»论坛 › 【数学研究】 › 难题征解 › n×n方格网中，最多可以选出多少个点，满足任意三点都不 ...
12下一页
返回列表 发新帖
查看: 56744|回复: 20

[提问] n×n方格网中，最多可以选出多少个点，满足任意三点都不共线？

[复制链接]
lsr314
发表于 2019-6-4 17:40:42 | 显示全部楼层 |阅读模式

马上注册，结交更多好友，享用更多功能，让你轻松玩转社区。

您需要 登录 才可以下载或查看，没有账号？欢迎注册

×
在n×n方格网中，最多可以选出多少个点，满足任意三点都不共线？
精华

最简单的n=3时，最多可选出6个。n=4就已经有点复杂了。
毋因群疑而阻独见　　毋任己意而废人言
毋私小惠而伤大体　　毋借公论以快私情
回复

使用道具 举报

.·.·.
发表于 2019-6-4 18:01:04 | 显示全部楼层
本帖最后由 .·.·. 于 2019-6-4 18:04 编辑

n=4是8个
你可以画一个圆
n=5就比较复杂了
感觉Key29会给出一个解答然后接上
“n=6就比较复杂了”
然后说不定mathe会给出一个解答然后接上
“n如果是复数的话就比较复杂了”



————————————————————————————————————————————————————————————————————————————————————————————————————

忽然意识到这个题难到爆炸
问集合{$1,2,3,...,n^2$}究竟能选出多少个数字保证任意三个数不构成等差数列
我们的解不比上面这个答案少，而不比2n多

问题是2n这个上界显然而且应该有不小的改善空间，另一个……似乎仍然是Open的问题

点评

.·.·.
……下面那段话想错了……试图编程然后编程结果告诉我，我想得太简单，“共线”比等差数列的约束要强很多  发表于 2019-6-4 19:29
lsr314
确实，n=4还是简单的，因为可以取到上界2n，n=5可能只能取到9  发表于 2019-6-4 19:04
毋因群疑而阻独见　　毋任己意而废人言
毋私小惠而伤大体　　毋借公论以快私情
回复 支持 反对

使用道具 举报

lsr314
 楼主| 发表于 2019-6-4 19:39:33 | 显示全部楼层
n=5可以取到10：

n=5.jpg
毋因群疑而阻独见　　毋任己意而废人言
毋私小惠而伤大体　　毋借公论以快私情
回复 支持 反对

使用道具 举报

lsr314
 楼主| 发表于 2019-6-4 20:07:01 | 显示全部楼层
n=6可以取到12：

n=6.jpg

点评

markfang2050
递归归纳法，这是某年北大自主招生试题。  发表于 2019-6-4 21:47
.·.·.
这个图可以推广到n=8。。所以有一个问题是，是否所有n=k都能推广到n=4k的情况  发表于 2019-6-4 21:28
毋因群疑而阻独见　　毋任己意而废人言
毋私小惠而伤大体　　毋借公论以快私情
回复 支持 反对

使用道具 举报

lsr314
 楼主| 发表于 2019-6-4 22:09:50 | 显示全部楼层
n=7取14：

n=7.jpg
毋因群疑而阻独见　　毋任己意而废人言
毋私小惠而伤大体　　毋借公论以快私情
回复

使用道具 举报

lsr314
 楼主| 发表于 2019-6-4 22:10:47 | 显示全部楼层
尽量让中间没有点出现，外面呈现一个环形，这样通过的概率比较大
毋因群疑而阻独见　　毋任己意而废人言
毋私小惠而伤大体　　毋借公论以快私情
回复 支持 反对

使用道具 举报

.·.·.
发表于 2019-6-4 22:21:42 | 显示全部楼层
本帖最后由 .·.·. 于 2019-6-5 00:14 编辑

……
程序写完了，炸得很可以
果然学统计的程序都不好
这是我搜索出来的一组解，有一定的对称性(0302代表在x=3,y=2的位置有一个点)
0000 0001 0100 0103 0203 0204 0301 0302 0402 0404
捕获.PNG
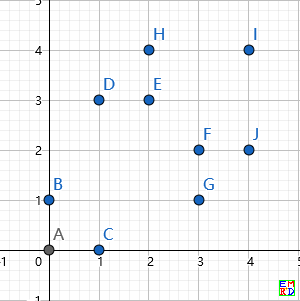
后面程序不知为何写着写着就放飞自我了（GCD写错……改过来就好了）
0002 0004 0103 0104 0200 0201 0302 0303 0401 0402
(0002,0302,0402共线)
N=5（对称意义下）的全部解（可能有重复，我没仔细筛）
  1. res10:0000 0001 0100 0103 0203 0204 0301 0302 0402 0404 .
  2. res10:0000 0001 0101 0103 0200 0204 0302 0304 0402 0403 .
  3. res10:0000 0002 0100 0101 0203 0204 0301 0304 0402 0403 .
  4. res10:0000 0002 0101 0104 0203 0204 0300 0301 0402 0403 .
  5. res10:0000 0002 0102 0103 0200 0201 0301 0304 0403 0404 .
  6. res10:0000 0002 0102 0104 0200 0201 0303 0304 0401 0403 .
  7. res10:0000 0003 0101 0103 0200 0204 0302 0304 0401 0402 .
  8. res10:0001 0002 0100 0102 0200 0204 0301 0303 0403 0404 .
  9. res10:0001 0002 0100 0103 0200 0201 0303 0304 0402 0404 .
  10. res10:0001 0002 0100 0104 0203 0204 0300 0301 0402 0403 .
  11. res10:0001 0002 0102 0104 0200 0204 0300 0303 0401 0403 .
  12. res10:0001 0002 0102 0104 0200 0204 0301 0303 0400 0403 .
  13. res10:0001 0002 0103 0104 0200 0201 0300 0303 0402 0404 .
  14. res10:0001 0002 0103 0104 0200 0201 0300 0304 0402 0403 .
  15. res10:0001 0003 0100 0101 0203 0204 0300 0302 0402 0404 .
  16. res10:0001 0003 0100 0103 0200 0204 0302 0304 0401 0402 .
  17. res10:0001 0003 0101 0104 0200 0204 0300 0302 0402 0403 .
  18. res10:0001 0003 0103 0104 0200 0201 0302 0304 0400 0402 .
  19. res10:0001 0003 0103 0104 0200 0204 0300 0302 0401 0402 .
  20. res10:0001 0004 0101 0103 0200 0204 0300 0302 0402 0403 .
  21. res10:0002 0003 0100 0101 0203 0204 0300 0304 0401 0402 .
  22. res10:0002 0003 0100 0101 0203 0204 0301 0304 0400 0402 .
  23. res10:0002 0003 0100 0102 0200 0204 0301 0303 0401 0404 .
  24. res10:0002 0003 0100 0102 0200 0204 0301 0304 0401 0403 .
  25. res10:0002 0003 0100 0104 0200 0201 0303 0304 0401 0402 .
  26. res10:0002 0003 0101 0104 0203 0204 0300 0301 0400 0402 .
  27. res10:0002 0003 0102 0104 0200 0204 0301 0303 0400 0401 .
  28. res10:0002 0003 0103 0104 0200 0201 0300 0304 0401 0402 .
  29. res10:0002 0004 0100 0102 0203 0204 0300 0301 0401 0403 .
  30. res10:0002 0004 0100 0102 0203 0204 0301 0303 0400 0401 .
  31. res10:0002 0004 0100 0103 0200 0201 0303 0304 0401 0402 .
  32. res10:0002 0004 0100 0104 0200 0202 0301 0303 0401 0403 .
  33. res10:0002 0004 0101 0102 0203 0204 0300 0301 0400 0403 .
  34. res10:0002 0004 0101 0102 0203 0204 0300 0303 0400 0401 .
  35. res10:0002 0004 0103 0104 0200 0201 0300 0303 0401 0402 .
复制代码
  1. #define N 9
  2.   #define stop (N-(N/2))  // maybe N-(N+1)/2 is more sutiable since it will produce less bad results.
  3.   #define N2 (N*N)
  4.   #define N8 (N<<8)
  5.   #define NN ((N<<8)|N)
  6.   #define UB (2*N+1) // UpperBound
  7.   #define at2(x,y) a[N*(x)+(y)]
  8.   #define at(x)   a[N*(((x)&0xFF00)>>8)+(x)&0xFF]
  9.   #define inRange(x)((N8>((unsigned short)(x)))&(N>(unsigned char)((x)&0xFF)))
  10. //  #define gt(x,y) (((x)>(y))&(char)((x)&0xFF-(y)&0xFF)>0)
  11. //  #define inRange(y) gt(y,0)&gt(NN,y)
  12. extern int printf(const char*,...);
  13. unsigned char a[N2+5000];
  14. unsigned short loc[UB+5000];
  15. int max=0;
  16. int cur=0;

  18. unsigned short divgcd(unsigned short x){
  19.   if(x<128){return 1;}
  20.   if(x&255){
  21.     switch(x){//1~10 only
  22. //2xx
  23.     case 0x1F6:return 0xFB;
  24.     case 0x1F8:return 0xFC;
  25.     case 0x1FA:return 0xFD;
  26.     case 0x1FC:return 0xFE;
  27.     case 0x1FE:return 0xFF;
  28.     case 0x202:return 0x101;
  29.     case 0x204:return 0x102;
  30.     case 0x206:return 0x103;
  31.     case 0x208:return 0x104;
  32.     case 0x20A:return 0x105;
  33. //3xx
  34.     case 0x2F7:return 0xFD;
  35.     case 0x2FA:return 0xFE;
  36.     case 0x2FD:return 0xFF;
  37.     case 0x303:return 0x101;
  38.     case 0x306:return 0x102;
  39.     case 0x309:return 0x103;
  40. //4xx
  41.     case 0x3F6:return 0x1FB;
  42.     case 0x3F8:return 0xFF;
  43.     case 0x3FA:return 0x1FD;
  44.     case 0x3FC:return 0xFF;
  45.     case 0x3FE:return 0x1FF;
  46.     case 0x402:return 0x201;
  47.     case 0x404:return 0x101;
  48.     case 0x406:return 0x203;
  49.     case 0x408:return 0x102;
  50.     case 0x40A:return 0x205;
  51. //5xx
  52.     case 0x4F6:return 0xFE;
  53.     case 0x4FB:return 0xFF;
  54.     case 0x505:return 0x101;
  55.     case 0x50A:return 0x102;
  56. //6xx
  57.     case 0x5F6:return 0x2FB;
  58.     case 0x5F7:return 0x1FD;
  59.     case 0x5F8:return 0x2FC;
  60.     case 0x5FA:return 0xFF;
  61.     case 0x5FC:return 0x2FE;
  62.     case 0x5FD:return 0x1FF;
  63.     case 0x5FE:return 0x3FF;
  64.     case 0x602:return 0x301;
  65.     case 0x603:return 0x201;
  66.     case 0x604:return 0x302;
  67.     case 0x606:return 0x101;
  68.     case 0x608:return 0x304;
  69.     case 0x609:return 0x203;
  70.     case 0x60A:return 0x305;
  71. //7xx
  72.     case 0x6F9:return 0xFF;
  73.     case 0x707:return 0x101;
  74. //8xx
  75.     case 0x7F6:return 0x3FB;
  76.     case 0x7F8:return 0xFF;
  77.     case 0x7FA:return 0x3FD;
  78.     case 0x7FC:return 0x1FF;
  79.     case 0x7FE:return 0x3FF;
  80.     case 0x802:return 0x401;
  81.     case 0x804:return 0x201;
  82.     case 0x806:return 0x403;
  83.     case 0x808:return 0x101;
  84.     case 0x80A:return 0x405;
  85. //9xx
  86.     case 0x8F7:return 0xFF;
  87.     case 0x8FA:return 0x2FE;
  88.     case 0x8FD:return 0x2FF;
  89.     case 0x903:return 0x301;
  90.     case 0x906:return 0x302;
  91.     case 0x909:return 0x101;
  92. //Axx
  93.     case 0x9F6:return 0xFF;
  94.     case 0x9FB:return 0x1FF;
  95.     case 0x9FE:return 0x4FF;
  96.     case 0xA02:return 0x501;
  97.     case 0xA05:return 0x201;
  98.     case 0xA0A:return 0x101;
  99.     default:return x;
  100.     }
  101.   }else{return 256;}
  102. }

  104. void add(unsigned short x){
  105. //  printf("\ncur%d+%04x:",cur,x);
  106.   at(x)+=1;
  107.   for(int i=0;i<cur;i++){
  108.     unsigned short tmp=divgcd(x-loc[i]);//printf("\n %d::%04x-%04x=%04x:",i,x,loc[i],tmp);
  109.     for(short y=x+tmp;inRange(y);y+=tmp){/*printf("+%04x",y);*/at(y)+=1;}
  110.   }
  111.   loc[cur]=x;
  112.   cur++;
  113. }
  114. void remove(unsigned short x){
  115. //  printf("\ncur%d-%04x:",cur,x);
  116.   cur--;
  117. //loc[cur]=0;
  118.   for(int i=0;i<cur;i++){
  119.     unsigned short tmp=divgcd(x-loc[i]);//printf("\n %d::%04x-%04x=%04x:",i,x,loc[i],tmp);
  120.     for(short y=x+tmp;inRange(y);y+=tmp){/*printf("-%04x",y);*/at(y)-=1;}
  121.   }
  122.   at(x)-=1;
  123. }
  124. //#include<stdlib.h>

  126. void find(unsigned short x){
  127. //  printf("\n:find%d.",cur);
  128. //unsigned char aaa[N2];
  129. //for(int i=0;i<N2;i++)aaa[i]=a[i];
  130.   add(x);
  131.   for(unsigned short y=x;y<N8;y++){
  132.     if((y&0xFF)==N){y&=0xFF00;y+=256;}// no need to break since it is a legal state.
  133.     if(!at(y)){find(y);}
  134.   }
  135.   if(max<cur){
  136.     max=cur;
  137.     printf("res%d:",cur);
  138.     for(int i=0;i<cur;i++)printf("%04x ",loc[i]);
  139.     printf(".\n");
  140.   }
  141.   remove(x);
  142. //for(int i=0;i<N2;i++)if(aaa[i]!=a[i]){exit(printf("!"));}
  143. }

  145. void main(){
  146.   for(int i=0;i<N2;i++)a[i]=0;
  147.   a[N2]=1;//ignore N<<8 illegal.
  148. //  printf("%04x %04x %04x %04x %04x %04x\n",divgcd(0x6652),divgcd(0x0103),divgcd(0x0301),divgcd(0x0202),divgcd(0x0204),divgcd(0x0005));
  149.   for(int i=0;i<stop;i++){find(i);}
  150. }//但愿GCD函数不再出错……
复制代码


————————————————————

毕竟我们一贯以来都把BUG视为strong regularizer……
Note:N=6,7的GCD函数存在错误
N=6

  1. res12:0000 0001 0101 0104 0204 0205 0300 0305 0402 0403 0502 0503 .
  2. res12:0000 0001 0103 0104 0200 0202 0302 0305 0401 0405 0503 0504 .
  3. res12:0000 0001 0103 0105 0201 0204 0300 0302 0404 0405 0502 0503 .
  4. res12:0000 0001 0103 0105 0202 0204 0300 0302 0401 0405 0503 0504 .
  5. res12:0000 0001 0104 0105 0200 0204 0302 0305 0401 0403 0502 0503 .
  6. res12:0000 0002 0101 0104 0203 0205 0300 0301 0403 0405 0502 0504 .
  7. res12:0000 0002 0101 0104 0204 0205 0300 0301 0403 0405 0502 0503 .
  8. res12:0000 0002 0102 0104 0200 0201 0304 0305 0401 0403 0503 0505 .
  9. res12:0000 0002 0103 0104 0201 0205 0300 0301 0404 0405 0502 0503 .
  10. res12:0000 0002 0104 0105 0201 0204 0300 0301 0403 0405 0502 0503 .
  11. res12:0000 0002 0104 0105 0201 0205 0300 0301 0403 0404 0502 0503 .
  12. res12:0000 0003 0100 0102 0203 0205 0301 0305 0402 0404 0501 0504 .
  13. res12:0000 0003 0100 0104 0202 0203 0301 0305 0402 0405 0501 0504 .
  14. res12:0000 0003 0101 0105 0203 0205 0302 0304 0400 0402 0501 0504 .
  15. res12:0000 0003 0102 0103 0200 0205 0301 0305 0401 0404 0502 0504 .
  16. res12:0000 0003 0102 0103 0200 0205 0304 0305 0401 0402 0501 0504 .
  17. res12:0000 0004 0102 0104 0201 0205 0301 0305 0400 0403 0502 0503 .
  18. res12:0000 0004 0102 0105 0202 0205 0300 0301 0401 0403 0503 0504 .
  19. res12:0000 0004 0103 0104 0200 0201 0302 0305 0401 0405 0502 0503 .
  20. res12:0001 0002 0100 0104 0200 0202 0303 0305 0401 0405 0503 0504 .
  21. res12:0001 0002 0100 0104 0200 0204 0302 0303 0401 0405 0503 0505 .
  22. res12:0001 0002 0100 0104 0203 0205 0301 0303 0400 0402 0504 0505 .
  23. res12:0001 0002 0102 0104 0200 0205 0300 0305 0401 0403 0503 0504 .
  24. res12:0001 0002 0102 0105 0204 0205 0300 0301 0400 0403 0503 0504 .
  25. res12:0001 0002 0104 0105 0200 0202 0303 0305 0400 0401 0503 0504 .
  26. res12:0001 0002 0104 0105 0200 0204 0300 0302 0401 0403 0503 0505 .
  27. res12:0001 0002 0104 0105 0201 0205 0300 0303 0402 0404 0500 0503 .
  28. res12:0001 0002 0104 0105 0204 0205 0300 0301 0400 0403 0502 0503 .
  29. res12:0001 0003 0100 0104 0201 0203 0300 0305 0402 0404 0502 0505 .
  30. res12:0001 0003 0101 0104 0200 0204 0300 0305 0402 0403 0502 0505 .
  31. res12:0001 0003 0101 0105 0203 0205 0300 0302 0400 0404 0502 0504 .
  32. res12:0001 0003 0101 0105 0204 0205 0300 0302 0403 0404 0500 0502 .
  33. res12:0001 0003 0102 0105 0200 0204 0301 0305 0400 0403 0502 0504 .
  34. res12:0001 0003 0103 0104 0200 0201 0300 0305 0402 0404 0502 0505 .
  35. res12:0001 0003 0103 0105 0200 0201 0304 0305 0400 0402 0502 0504 .
  36. res12:0001 0003 0104 0105 0200 0203 0300 0305 0402 0404 0501 0502 .
  37. res12:0001 0003 0104 0105 0201 0202 0303 0305 0400 0402 0500 0504 .
  38. res12:0001 0004 0100 0101 0204 0205 0300 0305 0402 0403 0502 0503 .
  39. res12:0001 0004 0100 0103 0200 0204 0302 0303 0401 0405 0502 0505 .
  40. res12:0001 0004 0100 0105 0201 0205 0300 0303 0402 0404 0502 0503 .
  41. res12:0001 0004 0101 0102 0204 0205 0300 0305 0400 0403 0502 0503 .
  42. res12:0001 0004 0101 0102 0204 0205 0300 0305 0402 0403 0500 0503 .
  43. res12:0001 0004 0101 0102 0204 0205 0303 0305 0400 0403 0500 0502 .
  44. res12:0001 0004 0101 0103 0200 0204 0300 0302 0403 0405 0502 0505 .
  45. res12:0001 0004 0102 0104 0201 0205 0303 0305 0400 0402 0500 0503 .
  46. res12:0001 0004 0102 0105 0201 0205 0302 0303 0400 0404 0500 0503 .
  47. res12:0001 0004 0102 0105 0204 0205 0300 0301 0400 0403 0502 0503 .
  48. res12:0001 0004 0103 0104 0200 0201 0300 0305 0402 0403 0502 0505 .
  49. res12:0001 0004 0103 0105 0200 0201 0303 0305 0402 0404 0500 0502 .
  50. res12:0002 0003 0100 0101 0203 0205 0301 0304 0400 0402 0504 0505 .
  51. res12:0002 0003 0100 0101 0204 0205 0300 0304 0401 0402 0503 0505 .
  52. res12:0002 0003 0100 0102 0204 0205 0301 0304 0400 0401 0503 0505 .
  53. res12:0002 0003 0100 0104 0200 0201 0304 0305 0401 0405 0502 0503 .
  54. res12:0002 0003 0100 0105 0200 0203 0304 0305 0401 0402 0501 0504 .
  55. res12:0002 0003 0101 0105 0204 0205 0300 0301 0400 0403 0502 0504 .
  56. res12:0002 0003 0101 0105 0204 0205 0300 0301 0400 0404 0502 0503 .
  57. res12:0002 0003 0103 0104 0200 0201 0300 0301 0404 0405 0502 0505 .
  58. res12:0002 0003 0103 0105 0200 0201 0300 0301 0404 0405 0502 0504 .
  59. res12:0002 0003 0103 0105 0200 0201 0300 0304 0404 0405 0501 0502 .
  60. res12:0002 0003 0103 0105 0201 0202 0300 0304 0404 0405 0500 0501 .
  61. res12:0002 0003 0104 0105 0200 0201 0300 0304 0402 0403 0501 0505 .
  62. res12:0002 0003 0104 0105 0200 0201 0303 0305 0401 0402 0500 0504 .
  63. res12:0002 0004 0100 0102 0203 0205 0301 0305 0400 0401 0503 0504 .
  64. res12:0002 0004 0100 0102 0204 0205 0300 0301 0403 0405 0501 0503 .
  65. res12:0002 0004 0100 0103 0201 0205 0300 0304 0402 0405 0501 0503 .
  66. res12:0002 0004 0100 0104 0200 0202 0303 0305 0401 0405 0501 0503 .
  67. res12:0002 0004 0100 0104 0202 0205 0301 0303 0403 0405 0500 0501 .
  68. res12:0002 0004 0100 0104 0202 0205 0301 0305 0401 0403 0500 0503 .
  69. res12:0002 0004 0100 0105 0202 0205 0300 0301 0403 0404 0501 0503 .
  70. res12:0002 0004 0101 0104 0201 0205 0300 0305 0402 0403 0500 0503 .
  71. res12:0002 0004 0101 0104 0203 0205 0300 0301 0400 0405 0502 0503 .
  72. res12:0002 0004 0101 0105 0202 0204 0300 0301 0403 0405 0500 0503 .
  73. res12:0002 0004 0101 0105 0204 0205 0300 0301 0400 0403 0502 0503 .
  74. res12:0002 0004 0103 0104 0200 0201 0300 0302 0401 0405 0503 0505 .
  75. res12:0002 0005 0100 0103 0203 0205 0301 0304 0400 0402 0501 0504 .
  76. res12:0002 0005 0101 0105 0202 0203 0300 0304 0400 0403 0501 0504 .
  77. res12:0002 0005 0102 0103 0200 0205 0300 0301 0403 0404 0501 0504 .
  78. res12:0002 0005 0102 0103 0200 0205 0300 0304 0401 0404 0501 0503 .
  79. res12:0002 0005 0103 0104 0200 0205 0300 0301 0403 0404 0501 0502 .
  80. res12:0002 0005 0103 0105 0200 0202 0300 0304 0401 0403 0501 0504 .
复制代码
N=7
(数量优点爆炸，算得有点慢)
  1. res14:0000 0001 0102 0104 0205 0206 0301 0305 0400 0403 0502 0504 0603 0606 .
  2. res14:0000 0002 0101 0102 0205 0206 0301 0304 0400 0406 0503 0504 0603 0605 .
  3. res14:0000 0002 0101 0102 0205 0206 0301 0305 0400 0403 0504 0506 0603 0604 .
  4. res14:0000 0002 0102 0105 0205 0206 0300 0301 0403 0406 0501 0504 0603 0604 .
  5. res14:0000 0002 0104 0105 0200 0202 0304 0306 0401 0403 0501 0506 0603 0605 .
  6. res14:0000 0002 0104 0105 0201 0203 0300 0306 0403 0405 0501 0502 0604 0606 .
  7. res14:0000 0002 0105 0106 0202 0204 0301 0304 0401 0403 0500 0506 0603 0605 .
  8. res14:0000 0003 0101 0105 0205 0206 0302 0304 0400 0401 0504 0506 0602 0603 .
  9. res14:0000 0003 0102 0105 0200 0205 0302 0304 0401 0406 0501 0504 0603 0606 .
  10. res14:0000 0003 0102 0105 0205 0206 0302 0304 0400 0401 0501 0504 0603 0606 .
  11. res14:0000 0003 0102 0105 0205 0206 0302 0304 0401 0406 0501 0504 0600 0603 .
  12. res14:0000 0003 0103 0105 0200 0201 0304 0306 0405 0406 0501 0502 0602 0604 .
  13. res14:0000 0003 0104 0106 0201 0206 0302 0304 0401 0405 0503 0505 0600 0602 .
  14. res14:0000 0004 0101 0103 0200 0201 0304 0306 0405 0406 0502 0503 0602 0605 .
  15. res14:0000 0004 0101 0103 0200 0201 0305 0306 0403 0405 0502 0506 0602 0604 .
  16. res14:0000 0004 0101 0104 0203 0206 0300 0306 0403 0405 0501 0502 0602 0605 .
  17. res14:0000 0004 0103 0104 0201 0205 0300 0302 0401 0405 0503 0506 0602 0606 .
  18. res14:0000 0004 0103 0106 0201 0203 0305 0306 0401 0405 0500 0502 0602 0604 .
  19. res14:0000 0004 0104 0105 0200 0202 0301 0306 0403 0406 0501 0502 0603 0605 .
  20. res14:0000 0004 0104 0106 0202 0203 0301 0306 0403 0405 0501 0502 0600 0605 .
  21. res14:0000 0005 0104 0106 0201 0202 0304 0306 0403 0405 0501 0503 0600 0602 .
  22. res14:0001 0002 0102 0105 0200 0206 0300 0306 0403 0404 0504 0505 0601 0603 .
  23. res14:0001 0002 0103 0105 0203 0206 0300 0306 0400 0401 0504 0505 0602 0604 .
  24. res14:0001 0002 0104 0105 0200 0204 0301 0306 0400 0403 0502 0506 0603 0605 .
  25. res14:0001 0002 0104 0106 0200 0204 0300 0306 0402 0403 0501 0505 0603 0605 .
  26. res14:0001 0003 0100 0104 0203 0206 0300 0305 0402 0406 0501 0502 0604 0605 .
  27. res14:0001 0003 0100 0105 0203 0205 0300 0302 0404 0406 0501 0502 0604 0606 .
  28. res14:0001 0003 0100 0105 0204 0205 0300 0302 0401 0406 0503 0506 0602 0604 .
  29. res14:0001 0003 0101 0105 0200 0204 0304 0306 0400 0406 0502 0505 0602 0603 .
  30. res14:0001 0003 0101 0105 0203 0206 0302 0306 0400 0402 0504 0505 0600 0604 .
  31. res14:0001 0003 0102 0103 0200 0206 0302 0305 0400 0401 0504 0505 0604 0606 .
  32. res14:0001 0003 0102 0104 0200 0206 0301 0305 0400 0406 0502 0504 0603 0605 .
  33. res14:0001 0003 0102 0105 0200 0202 0305 0306 0404 0406 0500 0504 0601 0603 .
  34. res14:0001 0003 0103 0104 0204 0206 0300 0301 0400 0402 0505 0506 0602 0605 .
  35. res14:0001 0003 0103 0106 0200 0204 0300 0306 0402 0404 0501 0505 0602 0605 .
  36. res14:0001 0003 0103 0106 0201 0204 0300 0306 0402 0404 0500 0505 0602 0605 .
  37. res14:0001 0003 0104 0105 0200 0206 0301 0304 0400 0406 0502 0505 0602 0603 .
  38. res14:0001 0003 0104 0105 0204 0206 0300 0301 0400 0406 0502 0503 0602 0605 .
  39. res14:0001 0003 0105 0106 0200 0202 0304 0306 0400 0402 0504 0505 0601 0603 .
  40. res14:0001 0003 0105 0106 0205 0206 0300 0302 0400 0401 0503 0504 0602 0604 .
  41. res14:0001 0004 0100 0101 0204 0205 0305 0306 0400 0402 0503 0506 0602 0603 .
  42. res14:0001 0004 0100 0103 0204 0206 0300 0306 0402 0405 0501 0503 0602 0605 .
  43. res14:0001 0004 0100 0106 0204 0205 0305 0306 0401 0402 0500 0503 0602 0603 .
  44. res14:0001 0004 0101 0102 0205 0206 0300 0306 0400 0403 0504 0505 0602 0603 .
  45. res14:0001 0004 0101 0103 0204 0206 0300 0306 0402 0405 0500 0503 0602 0605 .
  46. res14:0001 0004 0101 0104 0200 0203 0300 0306 0403 0406 0502 0505 0602 0605 .
  47. res14:0001 0004 0101 0104 0200 0206 0300 0306 0403 0405 0502 0503 0602 0605 .
  48. res14:0001 0004 0101 0104 0203 0206 0300 0306 0400 0403 0502 0505 0602 0605 .
  49. res14:0001 0004 0101 0105 0203 0204 0300 0306 0400 0406 0502 0503 0602 0605 .
  50. res14:0001 0004 0102 0106 0204 0206 0300 0305 0402 0403 0500 0505 0601 0603 .
  51. res14:0001 0004 0103 0104 0200 0201 0300 0302 0405 0406 0503 0505 0602 0606 .
  52. res14:0001 0004 0103 0104 0200 0201 0300 0306 0405 0406 0502 0503 0602 0605 .
  53. res14:0001 0004 0103 0104 0200 0206 0300 0306 0402 0403 0501 0505 0602 0605 .
  54. res14:0001 0004 0103 0104 0200 0206 0300 0306 0403 0405 0501 0502 0602 0605 .
  55. res14:0001 0004 0103 0104 0201 0206 0300 0306 0402 0405 0500 0503 0602 0605 .
  56. res14:0001 0004 0103 0104 0201 0206 0300 0306 0402 0405 0502 0503 0600 0605 .
  57. res14:0001 0004 0103 0104 0201 0206 0300 0306 0402 0405 0503 0505 0600 0602 .
  58. res14:0001 0004 0103 0106 0201 0204 0300 0306 0402 0405 0500 0503 0602 0605 .
  59. res14:0001 0004 0104 0105 0200 0201 0305 0306 0400 0406 0502 0503 0602 0603 .
  60. res14:0001 0004 0104 0105 0201 0203 0300 0306 0400 0406 0502 0503 0602 0605 .
  61. res14:0001 0004 0104 0106 0200 0201 0305 0306 0400 0403 0502 0505 0602 0603 .
  62. res14:0001 0004 0104 0106 0200 0201 0305 0306 0403 0405 0502 0503 0600 0602 .
  63. res14:0001 0004 0104 0106 0200 0203 0301 0305 0400 0406 0502 0505 0602 0603 .
  64. res14:0001 0004 0104 0106 0201 0203 0305 0306 0400 0403 0502 0505 0600 0602 .
  65. res14:0001 0004 0105 0106 0202 0204 0300 0301 0405 0406 0500 0503 0602 0603 .
  66. res14:0001 0005 0100 0102 0205 0206 0302 0303 0404 0406 0500 0503 0601 0604 .
  67. res14:0001 0005 0100 0103 0202 0204 0300 0306 0402 0404 0501 0506 0603 0605 .
  68. res14:0001 0005 0100 0105 0203 0204 0300 0302 0404 0406 0502 0503 0601 0606 .
  69. res14:0001 0005 0100 0105 0203 0206 0300 0302 0404 0406 0502 0503 0601 0604 .
  70. res14:0001 0005 0101 0103 0203 0206 0302 0306 0400 0402 0504 0505 0600 0604 .
  71. res14:0001 0005 0102 0103 0200 0202 0300 0306 0404 0406 0501 0504 0603 0605 .
  72. res14:0001 0005 0102 0103 0200 0202 0300 0306 0404 0406 0503 0504 0601 0605 .
  73. res14:0001 0005 0102 0104 0200 0202 0305 0306 0400 0406 0503 0504 0601 0603 .
  74. res14:0001 0005 0102 0105 0200 0202 0300 0306 0404 0406 0503 0504 0601 0603 .
  75. res14:0001 0005 0102 0105 0202 0206 0300 0306 0400 0404 0503 0504 0601 0603 .
  76. res14:0001 0006 0100 0101 0204 0205 0300 0303 0405 0406 0502 0503 0602 0604 .
  77. res14:0002 0003 0100 0101 0205 0206 0302 0304 0400 0401 0505 0506 0603 0604 .
  78. res14:0002 0003 0100 0102 0203 0206 0301 0305 0400 0401 0504 0505 0604 0606 .
  79. res14:0002 0003 0100 0102 0205 0206 0301 0305 0400 0401 0504 0506 0603 0604 .
  80. res14:0002 0003 0100 0105 0204 0206 0301 0304 0400 0401 0505 0506 0602 0603 .
  81. res14:0002 0003 0100 0105 0204 0206 0301 0306 0400 0401 0504 0505 0602 0603 .
  82. res14:0002 0003 0100 0105 0205 0206 0300 0302 0401 0404 0501 0503 0604 0606 .
  83. res14:0002 0003 0100 0105 0205 0206 0301 0304 0400 0401 0504 0506 0602 0603 .
  84. res14:0002 0003 0100 0105 0205 0206 0302 0304 0400 0401 0501 0506 0603 0604 .
  85. res14:0002 0003 0101 0105 0203 0204 0300 0306 0400 0401 0505 0506 0602 0604 .
  86. res14:0002 0003 0101 0105 0203 0206 0300 0306 0400 0401 0504 0505 0602 0604 .
  87. res14:0002 0003 0101 0105 0203 0206 0304 0306 0400 0401 0504 0505 0600 0602 .
  88. res14:0002 0003 0101 0105 0204 0206 0300 0306 0400 0401 0503 0505 0602 0604 .
  89. res14:0002 0003 0101 0105 0205 0206 0300 0302 0400 0406 0501 0504 0603 0604 .
  90. res14:0002 0003 0101 0105 0205 0206 0302 0304 0400 0401 0504 0506 0600 0603 .
  91. res14:0002 0003 0101 0105 0205 0206 0302 0304 0400 0406 0501 0504 0600 0603 .
  92. res14:0002 0003 0102 0105 0200 0203 0305 0306 0400 0401 0501 0504 0604 0606 .
  93. res14:0002 0003 0102 0105 0200 0206 0301 0304 0400 0406 0504 0505 0601 0603 .
  94. res14:0002 0003 0102 0105 0200 0206 0301 0306 0400 0404 0504 0505 0601 0603 .
  95. res14:0002 0003 0102 0105 0200 0206 0304 0306 0400 0401 0501 0505 0603 0604 .
  96. res14:0002 0003 0102 0105 0200 0206 0304 0306 0400 0401 0504 0505 0601 0603 .
  97. res14:0002 0003 0102 0105 0200 0206 0304 0306 0400 0404 0501 0505 0601 0603 .
  98. res14:0002 0003 0102 0105 0200 0206 0305 0306 0400 0401 0501 0504 0603 0604 .
  99. res14:0002 0003 0102 0105 0203 0206 0305 0306 0400 0401 0500 0504 0601 0604 .
  100. res14:0002 0003 0102 0105 0203 0206 0305 0306 0400 0401 0501 0504 0600 0604 .
  101. res14:0002 0003 0102 0106 0200 0206 0304 0305 0400 0401 0501 0505 0603 0604 .
  102. res14:0002 0003 0103 0105 0201 0202 0300 0306 0404 0405 0500 0506 0601 0604 .
  103. res14:0002 0003 0103 0105 0201 0206 0300 0306 0402 0404 0500 0505 0601 0604 .
  104. res14:0002 0003 0103 0105 0205 0206 0300 0301 0400 0401 0504 0506 0602 0604 .
  105. res14:0002 0003 0103 0106 0200 0201 0300 0306 0404 0405 0501 0505 0602 0604 .
  106. res14:0002 0003 0103 0106 0205 0206 0300 0301 0400 0401 0504 0505 0602 0604 .
  107. res14:0002 0003 0104 0106 0200 0201 0300 0304 0405 0406 0501 0505 0602 0603 .
  108. res14:0002 0003 0104 0106 0200 0201 0302 0304 0405 0406 0501 0505 0600 0603 .
  109. res14:0002 0003 0105 0106 0200 0201 0302 0304 0405 0406 0500 0501 0603 0604 .
  110. res14:0002 0003 0105 0106 0200 0206 0302 0304 0400 0401 0501 0505 0603 0604 .
  111. res14:0002 0003 0105 0106 0201 0206 0300 0302 0401 0404 0503 0505 0600 0604 .
  112. res14:0002 0003 0105 0106 0205 0206 0300 0302 0401 0404 0501 0503 0600 0604 .
  113. res14:0002 0004 0100 0101 0205 0206 0300 0306 0401 0403 0503 0505 0602 0604 .
  114. res14:0002 0004 0100 0101 0205 0206 0300 0306 0402 0403 0501 0505 0603 0604 .
  115. res14:0002 0004 0100 0101 0205 0206 0304 0306 0400 0401 0503 0505 0602 0603 .
  116. res14:0002 0004 0100 0103 0200 0205 0304 0306 0401 0402 0501 0506 0603 0605 .
  117. res14:0002 0004 0100 0103 0201 0205 0300 0306 0401 0405 0503 0506 0602 0604 .
  118. res14:0002 0004 0100 0103 0205 0206 0300 0306 0401 0403 0501 0505 0602 0604 .
  119. res14:0002 0004 0100 0104 0201 0203 0300 0301 0405 0406 0503 0505 0602 0606 .
  120. res14:0002 0004 0100 0105 0204 0205 0301 0306 0400 0401 0503 0506 0602 0603 .
  121. res14:0002 0004 0101 0102 0205 0206 0300 0306 0400 0403 0501 0503 0604 0605 .
  122. res14:0002 0004 0101 0102 0205 0206 0300 0306 0400 0403 0501 0505 0603 0604 .
  123. res14:0002 0004 0101 0105 0201 0203 0300 0306 0405 0406 0500 0503 0602 0604 .
  124. res14:0002 0004 0101 0105 0203 0205 0300 0306 0400 0401 0503 0506 0602 0604 .
  125. res14:0002 0004 0101 0106 0202 0204 0300 0306 0403 0405 0501 0503 0600 0605 .
  126. res14:0002 0004 0102 0106 0203 0205 0305 0306 0400 0401 0500 0501 0603 0604 .
  127. res14:0002 0004 0103 0106 0200 0201 0300 0306 0403 0405 0501 0505 0602 0604 .
  128. res14:0002 0004 0103 0106 0201 0205 0300 0306 0401 0405 0500 0503 0602 0604 .
  129. res14:0002 0004 0104 0105 0201 0203 0300 0306 0403 0405 0501 0502 0600 0606 .
  130. res14:0002 0004 0105 0106 0200 0202 0301 0304 0401 0403 0500 0506 0603 0605 .
  131. res14:0002 0005 0100 0103 0202 0205 0300 0306 0401 0404 0503 0506 0601 0604 .
  132. res14:0002 0005 0101 0102 0203 0205 0300 0306 0400 0406 0501 0504 0603 0604 .
  133. res14:0002 0005 0101 0102 0203 0205 0300 0306 0400 0406 0503 0504 0601 0604 .
  134. res14:0002 0005 0101 0102 0203 0205 0300 0306 0403 0406 0501 0504 0600 0604 .
  135. res14:0002 0005 0101 0102 0203 0206 0300 0306 0400 0403 0504 0505 0601 0604 .
  136. res14:0002 0005 0101 0102 0205 0206 0300 0306 0400 0403 0501 0504 0603 0604 .
  137. res14:0002 0005 0101 0103 0205 0206 0300 0304 0400 0401 0503 0506 0602 0604 .
  138. res14:0002 0005 0101 0103 0205 0206 0300 0306 0400 0401 0503 0504 0602 0604 .
  139. res14:0002 0005 0101 0105 0202 0203 0300 0306 0400 0406 0501 0504 0603 0604 .
  140. res14:0002 0005 0101 0105 0202 0203 0300 0306 0400 0406 0503 0504 0601 0604 .
  141. res14:0002 0005 0101 0105 0203 0206 0300 0302 0400 0406 0501 0504 0603 0604 .
  142. res14:0002 0005 0102 0103 0200 0206 0300 0306 0401 0403 0504 0505 0601 0604 .
  143. res14:0002 0005 0102 0103 0200 0206 0300 0306 0403 0404 0501 0505 0601 0604 .
  144. res14:0002 0005 0102 0103 0200 0206 0301 0306 0400 0404 0504 0505 0601 0603 .
  145. res14:0002 0005 0102 0103 0205 0206 0300 0306 0400 0401 0503 0504 0601 0604 .
  146. res14:0002 0005 0102 0103 0205 0206 0300 0306 0400 0404 0501 0503 0601 0604 .
  147. res14:0002 0005 0102 0103 0205 0206 0300 0306 0401 0404 0500 0503 0601 0604 .
  148. res14:0002 0005 0102 0105 0200 0203 0300 0306 0403 0406 0501 0504 0601 0604 .
  149. res14:0002 0005 0102 0105 0200 0206 0300 0306 0403 0404 0501 0504 0601 0603 .
  150. res14:0002 0005 0102 0105 0203 0206 0300 0306 0400 0403 0501 0504 0601 0604 .
  151. res14:0002 0005 0102 0105 0204 0206 0300 0301 0400 0404 0503 0506 0601 0603 .
  152. res14:0002 0005 0103 0105 0202 0206 0300 0306 0401 0404 0500 0503 0601 0604 .
  153. res14:0002 0005 0104 0106 0200 0201 0304 0306 0403 0405 0501 0503 0600 0602 .
  154. res14:0002 0006 0101 0102 0203 0205 0300 0306 0401 0403 0504 0505 0600 0604 .
  155. res14:0002 0006 0101 0102 0204 0206 0300 0304 0400 0403 0501 0505 0603 0605 .
  156. res14:0002 0006 0101 0106 0202 0204 0300 0304 0403 0405 0500 0501 0603 0605 .
  157. res14:0002 0006 0102 0104 0200 0204 0301 0303 0400 0401 0505 0506 0603 0605 .
  158. res14:0002 0006 0102 0105 0200 0203 0300 0306 0401 0403 0504 0505 0601 0604 .
  159. res14:0002 0006 0103 0105 0205 0206 0300 0302 0400 0401 0503 0504 0601 0604 .
  160. res14:0003 0004 0100 0101 0204 0206 0305 0306 0400 0402 0501 0502 0603 0605 .
  161. res14:0003 0004 0100 0101 0204 0206 0305 0306 0400 0402 0502 0505 0601 0603 .
  162. res14:0003 0004 0100 0101 0205 0206 0302 0304 0400 0401 0505 0506 0602 0603 .
  163. res14:0003 0004 0100 0102 0204 0206 0301 0305 0400 0402 0501 0506 0603 0605 .
  164. res14:0003 0004 0100 0102 0204 0206 0301 0305 0400 0402 0505 0506 0601 0603 .
  165. res14:0003 0004 0100 0102 0205 0206 0301 0302 0400 0401 0505 0506 0603 0604 .
  166. res14:0003 0004 0100 0102 0205 0206 0301 0305 0400 0402 0504 0506 0601 0603 .
  167. res14:0003 0004 0100 0103 0204 0206 0300 0306 0401 0402 0501 0505 0602 0605 .
  168. res14:0003 0004 0101 0102 0205 0206 0301 0305 0400 0402 0504 0506 0600 0603 .
  169. res14:0003 0004 0101 0103 0204 0206 0300 0306 0401 0402 0500 0505 0602 0605 .
  170. res14:0003 0004 0101 0104 0200 0206 0301 0302 0400 0406 0502 0505 0603 0605 .
  171. res14:0003 0004 0101 0104 0200 0206 0301 0302 0405 0406 0502 0505 0600 0603 .
  172. res14:0003 0004 0101 0104 0201 0206 0300 0302 0400 0405 0505 0506 0602 0603 .
  173. res14:0003 0004 0101 0104 0201 0206 0302 0305 0400 0406 0502 0505 0600 0603 .
  174. res14:0003 0004 0101 0104 0203 0206 0300 0301 0400 0406 0502 0505 0602 0605 .
  175. res14:0003 0004 0101 0104 0203 0206 0300 0301 0405 0406 0502 0505 0600 0602 .
  176. res14:0003 0004 0101 0105 0200 0201 0304 0305 0400 0406 0502 0506 0602 0603 .
  177. res14:0003 0004 0101 0105 0200 0201 0304 0306 0400 0406 0502 0505 0602 0603 .
  178. res14:0003 0004 0101 0105 0200 0202 0305 0306 0402 0406 0500 0504 0601 0603 .
  179. res14:0003 0004 0101 0105 0200 0203 0300 0306 0405 0406 0501 0502 0602 0604 .
  180. res14:0003 0004 0101 0105 0200 0204 0301 0306 0400 0406 0502 0505 0602 0603 .
  181. res14:0003 0004 0101 0105 0201 0202 0300 0302 0405 0406 0500 0506 0603 0604 .
  182. res14:0003 0004 0101 0105 0201 0202 0300 0306 0405 0406 0500 0503 0602 0604 .
  183. res14:0003 0004 0101 0105 0201 0203 0300 0306 0405 0406 0500 0502 0602 0604 .
  184. res14:0003 0004 0101 0105 0201 0203 0304 0306 0400 0406 0502 0505 0600 0602 .
  185. res14:0003 0004 0101 0105 0201 0204 0300 0306 0400 0406 0502 0503 0602 0605 .
  186. res14:0003 0004 0101 0105 0202 0203 0300 0306 0405 0406 0500 0501 0602 0604 .
  187. res14:0003 0004 0101 0106 0200 0201 0300 0306 0403 0405 0502 0505 0602 0604 .
  188. res14:0003 0004 0101 0106 0200 0201 0302 0304 0405 0406 0500 0505 0602 0603 .
  189. res14:0003 0004 0101 0106 0200 0201 0302 0305 0405 0406 0500 0502 0603 0604 .
  190. res14:0003 0004 0101 0106 0201 0202 0300 0305 0405 0406 0500 0503 0602 0604 .
  191. res14:0003 0004 0101 0106 0203 0206 0301 0302 0400 0405 0504 0505 0600 0602 .
  192. res14:0003 0004 0102 0104 0203 0206 0301 0305 0400 0406 0501 0502 0600 0605 .
  193. res14:0003 0004 0103 0105 0200 0201 0300 0306 0405 0406 0501 0502 0602 0604 .
  194. res14:0003 0004 0103 0105 0200 0201 0304 0306 0405 0406 0500 0502 0601 0602 .
  195. res14:0003 0004 0103 0105 0200 0201 0304 0306 0405 0406 0501 0502 0600 0602 .
  196. res14:0003 0004 0103 0106 0200 0201 0300 0306 0402 0404 0501 0505 0602 0605 .
  197. res14:0003 0004 0103 0106 0201 0204 0300 0306 0401 0402 0500 0505 0602 0605 .
  198. res14:0003 0004 0103 0106 0201 0205 0300 0305 0401 0402 0500 0506 0602 0604 .
  199. res14:0003 0004 0104 0105 0200 0201 0301 0302 0400 0406 0502 0505 0603 0606 .
  200. res14:0003 0004 0104 0106 0200 0201 0301 0302 0405 0406 0502 0505 0600 0603 .
  201. res14:0003 0004 0104 0106 0200 0201 0301 0305 0400 0406 0502 0505 0602 0603 .
  202. res14:0003 0004 0104 0106 0200 0203 0301 0305 0405 0406 0501 0502 0600 0602 .
  203. res14:0003 0004 0104 0106 0200 0206 0300 0301 0403 0405 0501 0502 0602 0605 .
  204. res14:0003 0004 0104 0106 0201 0203 0301 0305 0400 0406 0502 0505 0600 0602 .
  205. res14:0003 0004 0104 0106 0201 0206 0300 0301 0400 0405 0502 0503 0602 0605 .
  206. res14:0003 0004 0104 0106 0201 0206 0301 0302 0400 0405 0502 0505 0600 0603 .
  207. res14:0003 0004 0104 0106 0201 0206 0301 0302 0400 0405 0503 0505 0600 0602 .
  208. res14:0003 0004 0105 0106 0201 0202 0300 0306 0402 0404 0500 0503 0601 0605 .
  209. res14:0003 0004 0105 0106 0201 0205 0300 0302 0400 0401 0503 0506 0602 0604 .
  210. res14:0003 0005 0100 0101 0202 0204 0305 0306 0400 0402 0501 0506 0603 0604 .
  211. res14:0003 0005 0100 0101 0202 0206 0305 0306 0400 0402 0501 0504 0603 0604 .
  212. res14:0003 0005 0100 0101 0204 0205 0300 0302 0402 0406 0501 0506 0603 0604 .
  213. res14:0003 0005 0100 0102 0204 0206 0301 0302 0404 0406 0501 0505 0600 0603 .
  214. res14:0003 0005 0100 0102 0205 0206 0302 0304 0401 0404 0501 0503 0600 0606 .
  215. res14:0003 0005 0101 0102 0200 0202 0305 0306 0400 0406 0501 0504 0603 0604 .
  216. res14:0003 0005 0101 0102 0200 0206 0302 0305 0400 0406 0501 0504 0603 0604 .
  217. res14:0003 0005 0101 0102 0200 0206 0302 0306 0400 0401 0504 0505 0603 0604 .
  218. res14:0003 0005 0101 0103 0205 0206 0300 0302 0400 0401 0504 0506 0602 0604 .
  219. res14:0003 0005 0101 0105 0200 0202 0302 0306 0400 0406 0501 0504 0603 0604 .
  220. res14:0003 0005 0101 0105 0201 0203 0300 0306 0402 0404 0500 0506 0602 0604 .
  221. res14:0003 0005 0101 0105 0202 0206 0300 0302 0400 0406 0501 0504 0603 0604 .
  222. res14:0003 0005 0101 0106 0201 0202 0304 0306 0400 0405 0500 0503 0602 0604 .
  223. res14:0003 0005 0101 0106 0202 0205 0300 0302 0400 0406 0501 0504 0603 0604 .
  224. res14:0003 0005 0102 0103 0200 0206 0304 0305 0400 0401 0502 0504 0601 0606 .
  225. res14:0003 0005 0102 0104 0200 0206 0301 0305 0400 0406 0502 0504 0601 0603 .
  226. res14:0003 0005 0102 0105 0200 0206 0302 0306 0400 0401 0501 0504 0603 0604 .
  227. res14:0003 0005 0102 0106 0200 0203 0301 0306 0400 0404 0504 0505 0601 0602 .
  228. res14:0003 0005 0102 0106 0202 0203 0305 0306 0400 0404 0500 0501 0601 0604 .
  229. res14:0003 0005 0102 0106 0203 0205 0301 0302 0400 0404 0501 0504 0600 0606 .
  230. res14:0003 0005 0102 0106 0203 0205 0301 0302 0400 0406 0501 0504 0600 0604 .
  231. res14:0003 0005 0102 0106 0203 0206 0301 0302 0400 0404 0501 0505 0600 0604 .
  232. res14:0003 0005 0103 0104 0200 0206 0300 0304 0405 0406 0501 0502 0601 0602 .
  233. res14:0003 0005 0103 0104 0200 0206 0301 0304 0405 0406 0501 0502 0600 0602 .
  234. res14:0003 0005 0103 0106 0200 0202 0304 0306 0404 0405 0500 0501 0601 0602 .
  235. res14:0003 0006 0101 0103 0201 0205 0304 0305 0400 0402 0504 0506 0600 0602 .
  236. res14:0003 0006 0101 0103 0205 0206 0300 0302 0400 0401 0504 0505 0602 0604 .
  237. res14:0003 0006 0101 0104 0200 0201 0302 0304 0405 0406 0502 0505 0600 0603 .
  238. res14:0003 0006 0101 0104 0200 0201 0304 0305 0400 0406 0502 0505 0602 0603 .
  239. res14:0003 0006 0101 0104 0200 0201 0304 0305 0405 0406 0500 0502 0602 0603 .
  240. res14:0003 0006 0101 0104 0200 0206 0301 0304 0400 0405 0502 0505 0602 0603 .
  241. res14:0003 0006 0101 0104 0200 0206 0302 0305 0401 0402 0504 0505 0600 0603 .
  242. res14:0003 0006 0101 0104 0201 0206 0302 0304 0400 0405 0502 0505 0600 0603 .
  243. res14:0003 0006 0102 0105 0200 0206 0301 0304 0400 0404 0502 0505 0601 0603 .
  244. res14:0003 0006 0103 0105 0201 0206 0300 0304 0400 0405 0502 0504 0601 0602 .
  245. res14:0003 0006 0104 0105 0200 0201 0301 0304 0400 0406 0502 0505 0602 0603 .
复制代码
n=8有解
n=9
  1. B:\>gcc play.c -O3 -march=native -o play2 && play2
  2. B:\>gcc play.c -O3 -march=native -o play2 && play2
  3. res13:0004 0005 0100 0101 0200 0201 0303 0304 0402 0502 0607 0608 0805 .
  4. res14:0004 0005 0100 0101 0200 0201 0303 0304 0402 0607 0608 0702 0803 0805 .
  5. res15:0004 0005 0100 0101 0200 0201 0303 0305 0408 0503 0508 0607 0702 0802 0804 .
  6. res16:0004 0005 0100 0101 0200 0201 0305 0306 0404 0408 0507 0508 0702 0703 0802 0806 .
  7. res17:0004 0005 0100 0101 0200 0201 0305 0306 0408 0506 0507 0602 0603 0703 0704 0802 0808 .
  8. res18:0004 0005 0100 0101 0204 0207 0300 0302 0407 0408 0506 0508 0601 0603 0703 0705 0802 0806 .
  9. ^C
  10. B:\>gcc play.c -O3 -march=native -o play2 && play2
  11. res15:0004 0005 0100 0101 0200 0201 0303 0304 0402 0409 0502 0607 0608 0905 0906 .
  12. res16:0004 0005 0100 0101 0200 0201 0303 0304 0402 0409 0607 0608 0702 0803 0905 0906 .
  13. res17:0004 0005 0100 0101 0200 0201 0303 0307 0402 0409 0508 0702 0708 0803 0809 0905 0906 .
  14. res18:0004 0005 0100 0101 0200 0201 0303 0307 0407 0409 0508 0603 0702 0708 0802 0806 0905 0906 .
  15. res19:0004 0005 0100 0101 0200 0202 0305 0307 0409 0501 0507 0603 0604 0702 0708 0803 0809 0906 0908 .
  16. res20:0004 0005 0100 0101 0205 0208 0306 0308 0400 0402 0507 0509 0602 0603 0701 0709 0803 0807 0904 0906 .
  17. ^C
复制代码
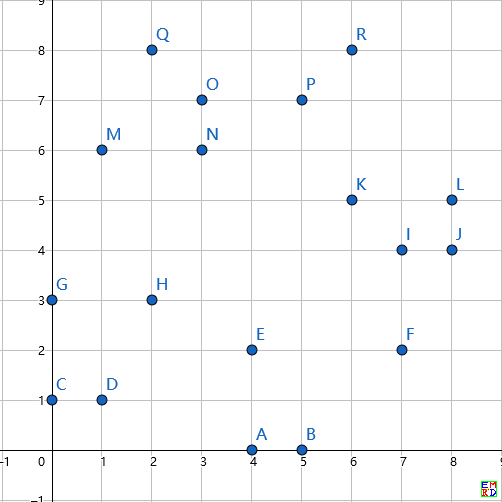
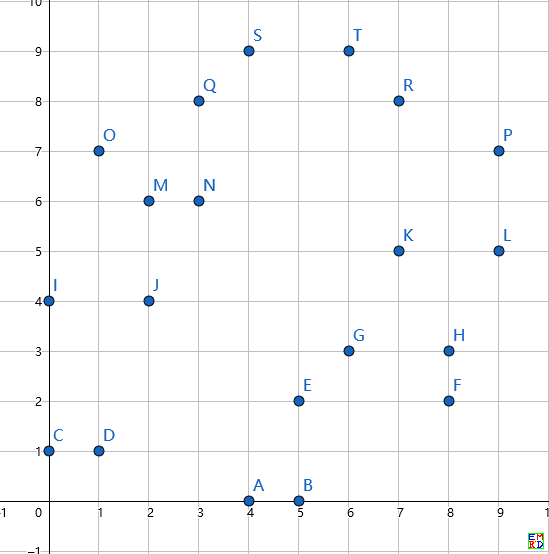捕获.PNG
捕获.PNG 倒着搜似乎快一点
  1. B:\>for /l %i in (5,1,10) do @(start /b play%i)
  2. res17:0005 0006 0100 0101 0200 0201 0303 0304 0409 040a 0502 0503 0607 0608 0802 0a05 0a07 .
  3. res18:0005 0006 0100 0101 0200 0201 0303 0304 0409 040a 0502 0608 0704 0708 080a 0907 0a02 0a03 .
  4. res19:0005 0006 0100 0101 0200 0201 0303 0304 0409 040a 0608 0702 0703 0802 080a 0906 0907 0a05 0a07 .
  5. res16:0006 0007 0100 0101 0200 0201 0303 0304 0409 040a 0503 0607 0608 0802 0902 0a05 .
  6. res18:0006 0007 0100 0101 0200 0201 0303 0304 0409 040a 0503 0608 0708 0802 080a 0902 0904 0a05 .
  7. res19:0006 0007 0100 0101 0200 0201 0303 0304 0409 040a 0604 0608 0702 0703 0805 0809 0902 0906 0a05 .
  8. res14:0007 0008 0100 0101 0200 0201 0303 0304 0402 0409 0602 0607 0903 0905 .
  9. res17:0007 0008 0100 0101 0200 0201 0303 0304 0402 0409 0602 0608 0805 0809 0903 0905 0a07 .
  10. res18:0007 0008 0100 0101 0200 0201 0303 0304 0409 040a 0503 0608 0802 0809 0902 0904 0a05 0a07 .

  12. B:\>res15:0008 0009 0100 0101 0200 0201 0303 0304 0402 0409 0502 0607 0608 0905 0906 .
  13. res16:0008 0009 0100 0101 0200 0201 0303 0304 0402 0409 0502 0608 0905 090a 0a03 0a07 .
  14. res17:0008 0009 0100 0101 0200 0201 0303 0304 0402 040a 0602 0608 0805 0809 0903 0904 0a07 .
  15. res18:0008 0009 0100 0101 0200 0201 0303 0304 0409 040a 0502 0608 0704 0705 0902 090a 0a03 0a05 .
  16. res15:0009 000a 0100 0101 0200 0201 0303 0304 0409 040a 0502 0503 0602 0607 0a07 .
  17. res16:0009 000a 0100 0101 0200 0201 0303 0304 0409 040a 0502 0503 0602 0608 0708 0a05 .
  18. res17:0009 000a 0100 0101 0200 0201 0303 0304 0409 040a 0502 0602 0608 0704 0708 0907 0a05 .
  19. res18:0009 000a 0100 0101 0200 0201 0303 0304 0409 040a 0502 0608 0704 0708 0902 0907 0a03 0a05 .
  20. res15:000a 0100 0101 0200 0201 0303 0304 0409 040a 0502 0503 0602 0607 0a06 0a07 .
  21. res16:000a 0100 0101 0200 0201 0303 0304 0409 040a 0502 0602 0604 0809 0906 0a05 0a06 .
  22. res17:000a 0100 0101 0200 0201 0303 0304 0409 040a 0502 0608 0704 0705 0809 0902 0a03 0a05 .
  23. res18:000a 0100 0101 0200 0201 0303 0304 0409 040a 0602 0608 0703 0704 0809 0902 0906 0a05 0a08 .
  24. res19:0008 0009 0100 0101 0200 0201 0303 0305 0408 0502 0607 060a 0704 070a 0802 0809 0907 0a03 0a04 .
  25. res19:0007 0008 0100 0101 0200 0201 0303 0306 040a 0508 050a 0602 0607 0702 0705 0809 0903 0a05 0a06 .
  26. res19:0009 000a 0100 0101 0200 0201 0303 0307 0408 0409 050a 0702 0708 0803 0805 0905 0907 0a02 0a06 .
  27. res20:0006 0007 0100 0101 0200 0201 0303 0307 0409 0508 050a 0604 0702 0708 0809 080a 0902 0903 0a04 0a06 .
  28. res20:0005 0006 0100 0101 0200 0201 0303 0307 0409 0508 0602 0604 0708 070a 0809 080a 0902 0903 0a05 0a06 .
  29. res19:000a 0100 0101 0200 0201 0303 0307 0407 0409 0502 0508 0603 0705 0708 0809 080a 0905 0a02 0a04 .
  30. res20:0007 0008 0100 0101 0200 0201 0304 0306 040a 0509 0602 0607 0703 0709 0805 0808 0903 0906 0a02 0a05 .
  31. res20:0008 0009 0100 0101 0200 0201 0305 0306 0402 0408 0505 060a 0709 070a 0802 0803 0904 0906 0a03 0a07 .
  32. res21:0006 0007 0100 0101 0200 0201 0306 0308 0404 040a 0508 050a 0602 0703 0709 0805 0809 0902 0903 0a05 0a07 .
  33. res20:0009 000a 0100 0101 0200 0203 0303 0307 0408 0507 050a 0602 0608 0701 0702 0805 0809 0904 0906 0a06 .
  34. res21:0007 0008 0100 0101 0200 0203 0307 0309 0403 0405 0508 050a 0609 0701 0702 0806 080a 0902 0904 0a04 0a06 .
  35. res21:0005 0006 0100 0101 0200 0203 0307 0309 0405 0508 050a 0602 0604 0701 0702 0808 080a 0903 0904 0a06 0a07 .
  36. res20:000a 0100 0101 0200 0203 0303 0307 0408 0507 050a 0602 0608 0701 0702 0805 0809 0904 0906 0a06 0a09 .
  37. res22:0005 0006 0100 0101 0200 0208 0305 030a 0403 0409 0503 0507 0601 0609 0707 0708 0802 0804 0902 090a 0a04 0a06 .
复制代码
这样就有了n=11的情况
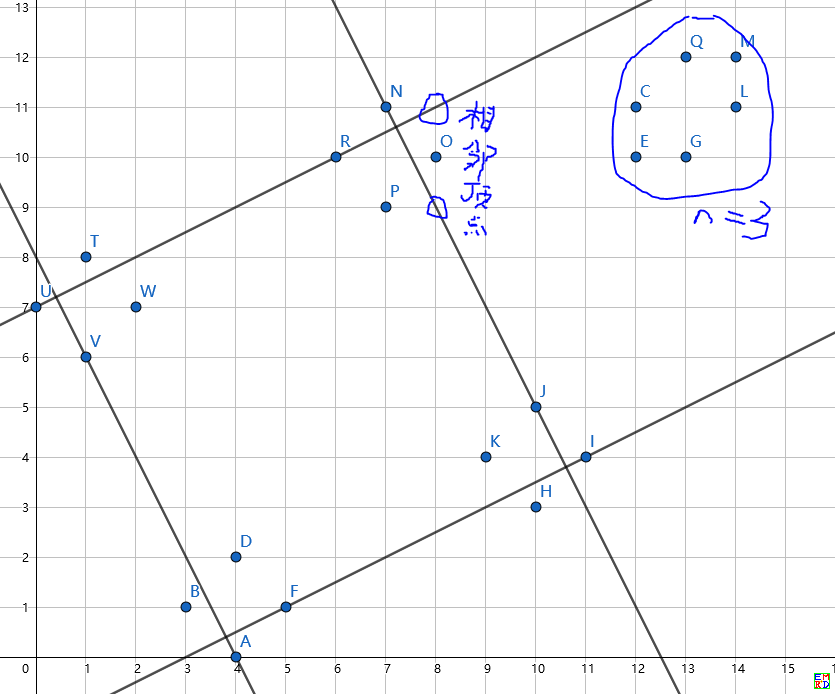
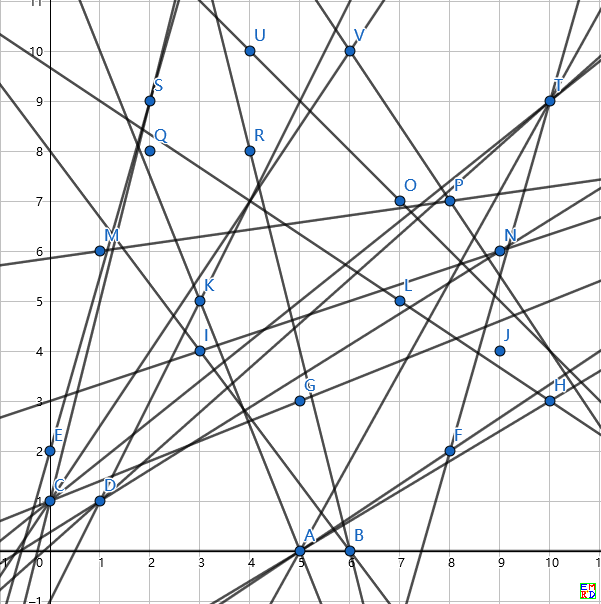
n=11尝试证明的确是共线的

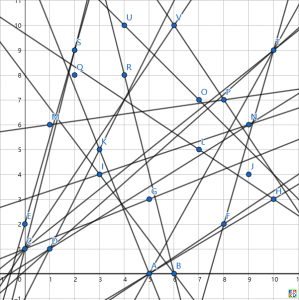
n=12不可用n=3(用n=2->n=8的方法)拼出的原因
捕获.PNG

捕获.PNG

点评

.·.·.
……你是怎么连上wiki的……我这里根本连不上……BTW利用对称性是有风险的，因为在利用对称性之前我们从未考虑过“循环共线”或者“反射共线”或者“轴对称共线”之类的情况——这些往往会阻止我们进行扩展  发表于 2019-6-5 14:28
lsr314
我是说图形本身对称，不是说直接用n/k的图形生成n，参考n=6,7,以及wiki里的10  发表于 2019-6-5 00:19
.·.·.
不能，我刚刚试过，n=12就是反例，不能由n=3像n=2->n=8那样生成  发表于 2019-6-5 00:08
lsr314
能否利用中心对称和轴对称找出一些比较对称的图行呢  发表于 2019-6-4 23:55
.·.·.
……我是直接暴力搜索的……根本不会ACM/NOIP里面的算法……  发表于 2019-6-4 22:42
下一页
毋因群疑而阻独见　　毋任己意而废人言
毋私小惠而伤大体　　毋借公论以快私情
回复 支持 反对

使用道具 举报

lsr314
 楼主| 发表于 2019-6-4 23:35:56 | 显示全部楼层
n=8取16（n=7和n=8均由幸福_狐狸给出）：

n=8.jpg
毋因群疑而阻独见　　毋任己意而废人言
毋私小惠而伤大体　　毋借公论以快私情
回复 支持 反对

使用道具 举报

.·.·.
发表于 2019-6-4 23:54:18 | 显示全部楼层
lsr314 发表于 2019-6-4 23:35
n=8取16（n=7和n=8均由幸福_狐狸给出）：

捕获.PNG

这是我说的n=6可以推广到n=8的原因
也是我说n=k推得n=4k是否可行的原因



毋因群疑而阻独见　　毋任己意而废人言
毋私小惠而伤大体　　毋借公论以快私情
回复 支持 反对

使用道具 举报

lsr314
 楼主| 发表于 2019-6-5 00:13:20 | 显示全部楼层
幸福_狐狸给出一个链接https://en.wikipedia.org/wiki/No-three-in-line_problem
里面提到n不超过46时，都是存在2n个点的解的。对于充分大的n，最佳结果小于2n，猜想大约为1.814n。
n=47的解并没有说不存在，大佬有兴趣可能试试。
毋因群疑而阻独见　　毋任己意而废人言
毋私小惠而伤大体　　毋借公论以快私情
回复 支持 反对

使用道具 举报

12下一页
返回列表 发新帖
高级模式
B Color Image Link Quote Code Smilies
您需要登录后才可以回帖 登录 | 欢迎注册

本版积分规则

小黑屋|手机版|数学研发网 ( 苏ICP备07505100号 )

GMT+8, 2024-4-20 10:33 , Processed in 0.084586 second(s), 20 queries .

Powered by Discuz! X3.5

© 2001-2024 Discuz! Team.

快速回复 返回顶部 返回列表