数学研发网设为首页收藏本站

切换到窄版

数学研发论坛»论坛 › 【综合大厅】 › 开心茶馆 › 在 6 座岛屿之间建造 5 座桥，使它们能够联通，请问有几 ...

12 3 4 / 4 页下一页

返回列表发新帖

查看: 39250|回复: 41

[转载] 在 6 座岛屿之间建造 5 座桥，使它们能够联通，请问有几种建桥方案？

发表于 2019-11-16 09:53:12 | 显示全部楼层 |阅读模式

马上注册，结交更多好友，享用更多功能，让你轻松玩转社区。

您需要登录才可以下载或查看，没有账号？欢迎注册

×

在 6 座岛屿之间建造 5 座桥，使它们能够联通，请问有几种建桥方案？

毋因群疑而阻独见　　毋任己意而废人言
毋私小惠而伤大体　　毋借公论以快私情

回复

使用道具举报

楼主| 发表于 2019-11-18 15:18:50 | 显示全部楼层

在 2 座岛屿之间建造 1 座桥，使它们能够联通，有 1 种建桥方案。
在 3 座岛屿之间建造 2 座桥，使它们能够联通，有 3 种建桥方案。
1：12=13
2：12=23
3：13=23
在 4 座岛屿之间建造 3 座桥，使它们能够联通，有 16 种建桥方案。
01：12,13=14
02：12,13=24
03：12,13=34
04：12,14=23
05：12,14=34
06：12,23=24
07：12,23=34
08：12,24=34
09：13,14=23
10：13,14=24
11：13,23=24
12：13,23=34
13：13,24=34
14：14,23=24
15：14,23=34
16：14,24=34
在 5 座岛屿之间建造 4 座桥，使它们能够联通，有 125 种建桥方案。
004：12,13,14=15,25,35,45
007：12,13,15=24,34,45
007：12,13,23=0
010：12,13,24=25,35,45
012：12,13,25=34,45
014：12,13,34=35,45
015：12,13,35=45

018：12,14,15=23,34,35
021：12,14,23=25,35,45
021：12,14,24=0
023：12,14,25=34,35
025：12,14,34=35,45
026：12,14,35=45

029：12,15,23=24,34,45
031：12,15,24=34,35
031：12,15,25=0
033：12,15,34=35,45
034：12,15,35=45

037：12,23,24=25,35,45
039：12,23,25=34,45
041：12,23,34=35,45
042：12,23,35=45

044：12,24,25=34,35
046：12,24,34=35,45
047：12,24,35=45
049：12,25,34=35,45
050：12,25,35=45
050：12,34,35=x

053：13,14,15=23,24,25
056：13,14,23=25,35,45
059：13,14,24=25,35,45
061：13,14,25=x,35,45
061：13,14,34=0
061：13,14,35=0

064：13,15,23=24,34,45
067：13,15,24=25,34,x,45
069：13,15,25=34,45
069：13,15,34=0
069：13,15,35=0

072：13,23,24=25,35,45
074：13,23,25=34,45
076：13,23,34=35,45
077：13,23,35=45

079：13,24,25=34,35,x
081：13,24,34=35,45
082：13,24,35=45
084：13,25,34=35,45
085：13,25,35=45
085：13,34,35=0

089：14,15,23=24,25,23,35,x
091：14,15,24=34,35
093：14,15,25=34,35
093：14,15,34=0
093：14,15,35=0

096：14,23,24=25,35,45
098：14,23,25=34,x,45
100：14,23,34=35,45
101：14,23,35=45

103：14,24,25=34,35
105：14,24,34=35,45
106：14,24,35=45
108：14,25,34=35,45
109：14,25,35=45
109：14,34,35=0

112：15,23,24=25,x,35,45
114：15,23,25=34,45
116：15,23,34=35,45
117：15,23,35=45

119：15,24,25=34,35
121：15,24,34=35,45
122：15,24,35=45
124：15,25,34=35,45
125：15,25,35=45
125：15,34,35=0

在 6 座岛屿之间建造 5 座桥，使它们能够联通，有 1296 种建桥方案。
1, 3, 16, 125, 1296, .......，可以是这串数吗？

毋因群疑而阻独见　　毋任己意而废人言
毋私小惠而伤大体　　毋借公论以快私情

回复支持反对

使用道具举报

发表于 2019-11-18 23:54:49 | 显示全部楼层

$a_n=n^(n-2)$?怎么证明？

点评

答案确定是1296吗？发表于 2019-11-19 22:11

毋因群疑而阻独见　　毋任己意而废人言
毋私小惠而伤大体　　毋借公论以快私情

回复支持 1 反对 0

使用道具举报

发表于 2019-11-23 09:16:43 | 显示全部楼层

本帖最后由 dlpg070 于 2019-11-23 10:39 编辑

王守恩发表于 2019-11-18 15:18
在 2 座岛屿之间建造 1 座桥，使它们能够联通，有 1 种建桥方案。
在 3 座岛屿之间建造 2 座桥，使它们能 ...

回复王守恩
用最笨方法，画图验证王守恩给出的数列是正确的
{1,3,16,125,1296}
图形演示时，为了清晰，各岛采用环形布局,
希望见到理论证明
下面给出部分数据图片，供欣赏

n=2全联通的方案数1
图片文件 2岛1桥.png

2岛1桥

2岛1桥

1 1 {{1,2}}

n=3全联通的方案数3
图片文件 3岛2桥.png

3岛2桥.png

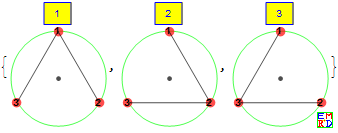
1 1 {{1,2},{1,3}}
2 2 {{1,2},{2,3}}
3 3 {{1,3},{2,3}}

n=4全联通的方案数16
图片文件 4岛3桥.png

4岛3桥.png

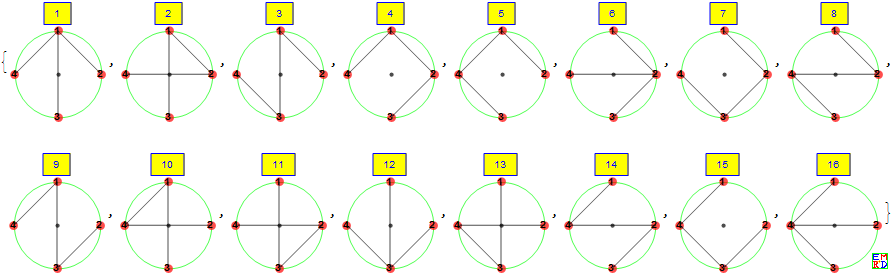
1 1 {{1,2},{1,3},{1,4}}
2 3 {{1,2},{1,3},{2,4}}
3 4 {{1,2},{1,3},{3,4}}
4 5 {{1,2},{1,4},{2,3}}
5 7 {{1,2},{1,4},{3,4}}
6 8 {{1,2},{2,3},{2,4}}
7 9 {{1,2},{2,3},{3,4}}
8 10 {{1,2},{2,4},{3,4}}
9 11 {{1,3},{1,4},{2,3}}
10 12 {{1,3},{1,4},{2,4}}
11 14 {{1,3},{2,3},{2,4}}
12 15 {{1,3},{2,3},{3,4}}
13 16 {{1,3},{2,4},{3,4}}
14 17 {{1,4},{2,3},{2,4}}
15 18 {{1,4},{2,3},{3,4}}
16 19 {{1,4},{2,4},{3,4}}

n=5全联通的方案数125
图片文件 5岛4桥.png(前50)

5岛4桥.png

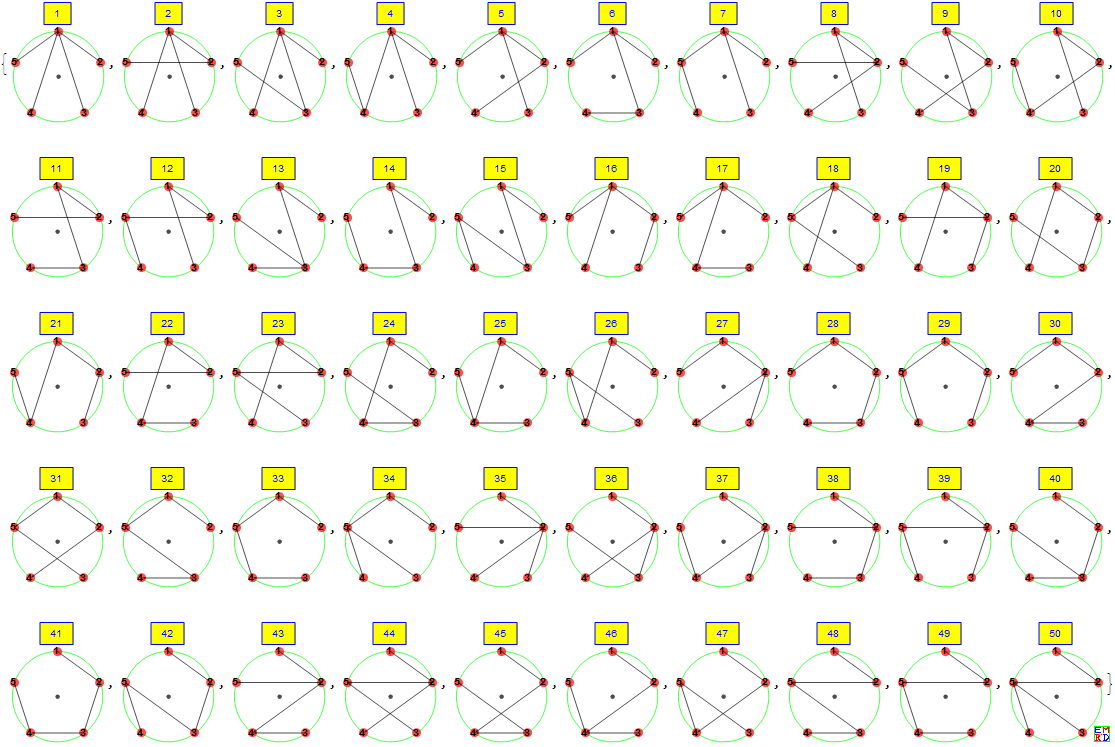
1 1 {{1,2},{1,3},{1,4},{1,5}}
2 4 {{1,2},{1,3},{1,4},{2,5}}
3 6 {{1,2},{1,3},{1,4},{3,5}}
4 7 {{1,2},{1,3},{1,4},{4,5}}
5 9 {{1,2},{1,3},{1,5},{2,4}}
6 11 {{1,2},{1,3},{1,5},{3,4}}
7 13 {{1,2},{1,3},{1,5},{4,5}}
8 19 {{1,2},{1,3},{2,4},{2,5}}
9 21 {{1,2},{1,3},{2,4},{3,5}}
10 22 {{1,2},{1,3},{2,4},{4,5}}
11 23 {{1,2},{1,3},{2,5},{3,4}}
12 25 {{1,2},{1,3},{2,5},{4,5}}
13 26 {{1,2},{1,3},{3,4},{3,5}}
14 27 {{1,2},{1,3},{3,4},{4,5}}
15 28 {{1,2},{1,3},{3,5},{4,5}}
16 29 {{1,2},{1,4},{1,5},{2,3}}
17 32 {{1,2},{1,4},{1,5},{3,4}}
18 33 {{1,2},{1,4},{1,5},{3,5}}
19 36 {{1,2},{1,4},{2,3},{2,5}}
20 38 {{1,2},{1,4},{2,3},{3,5}}
21 39 {{1,2},{1,4},{2,3},{4,5}}
22 44 {{1,2},{1,4},{2,5},{3,4}}
23 45 {{1,2},{1,4},{2,5},{3,5}}
24 47 {{1,2},{1,4},{3,4},{3,5}}
25 48 {{1,2},{1,4},{3,4},{4,5}}
26 49 {{1,2},{1,4},{3,5},{4,5}}
27 50 {{1,2},{1,5},{2,3},{2,4}}
28 52 {{1,2},{1,5},{2,3},{3,4}}
29 54 {{1,2},{1,5},{2,3},{4,5}}
30 56 {{1,2},{1,5},{2,4},{3,4}}
31 57 {{1,2},{1,5},{2,4},{3,5}}
32 62 {{1,2},{1,5},{3,4},{3,5}}
33 63 {{1,2},{1,5},{3,4},{4,5}}
34 64 {{1,2},{1,5},{3,5},{4,5}}
35 65 {{1,2},{2,3},{2,4},{2,5}}
36 67 {{1,2},{2,3},{2,4},{3,5}}
37 68 {{1,2},{2,3},{2,4},{4,5}}
38 69 {{1,2},{2,3},{2,5},{3,4}}
39 71 {{1,2},{2,3},{2,5},{4,5}}
40 72 {{1,2},{2,3},{3,4},{3,5}}
41 73 {{1,2},{2,3},{3,4},{4,5}}
42 74 {{1,2},{2,3},{3,5},{4,5}}
43 75 {{1,2},{2,4},{2,5},{3,4}}
44 76 {{1,2},{2,4},{2,5},{3,5}}
45 78 {{1,2},{2,4},{3,4},{3,5}}
46 79 {{1,2},{2,4},{3,4},{4,5}}
47 80 {{1,2},{2,4},{3,5},{4,5}}
48 81 {{1,2},{2,5},{3,4},{3,5}}
49 82 {{1,2},{2,5},{3,4},{4,5}}
50 83 {{1,2},{2,5},{3,5},{4,5}}
51 85 {{1,3},{1,4},{1,5},{2,3}}
52 86 {{1,3},{1,4},{1,5},{2,4}}
53 87 {{1,3},{1,4},{1,5},{2,5}}
54 92 {{1,3},{1,4},{2,3},{2,5}}
55 94 {{1,3},{1,4},{2,3},{3,5}}
56 95 {{1,3},{1,4},{2,3},{4,5}}
57 96 {{1,3},{1,4},{2,4},{2,5}}
58 98 {{1,3},{1,4},{2,4},{3,5}}
59 99 {{1,3},{1,4},{2,4},{4,5}}
60 101 {{1,3},{1,4},{2,5},{3,5}}
61 102 {{1,3},{1,4},{2,5},{4,5}}
62 106 {{1,3},{1,5},{2,3},{2,4}}
63 108 {{1,3},{1,5},{2,3},{3,4}}
64 110 {{1,3},{1,5},{2,3},{4,5}}
65 111 {{1,3},{1,5},{2,4},{2,5}}
66 112 {{1,3},{1,5},{2,4},{3,4}}
67 114 {{1,3},{1,5},{2,4},{4,5}}
68 115 {{1,3},{1,5},{2,5},{3,4}}
69 117 {{1,3},{1,5},{2,5},{4,5}}
70 121 {{1,3},{2,3},{2,4},{2,5}}
71 123 {{1,3},{2,3},{2,4},{3,5}}
72 124 {{1,3},{2,3},{2,4},{4,5}}
73 125 {{1,3},{2,3},{2,5},{3,4}}
74 127 {{1,3},{2,3},{2,5},{4,5}}
75 128 {{1,3},{2,3},{3,4},{3,5}}
76 129 {{1,3},{2,3},{3,4},{4,5}}
77 130 {{1,3},{2,3},{3,5},{4,5}}
78 131 {{1,3},{2,4},{2,5},{3,4}}
79 132 {{1,3},{2,4},{2,5},{3,5}}
80 134 {{1,3},{2,4},{3,4},{3,5}}
81 135 {{1,3},{2,4},{3,4},{4,5}}
82 136 {{1,3},{2,4},{3,5},{4,5}}
83 137 {{1,3},{2,5},{3,4},{3,5}}
84 138 {{1,3},{2,5},{3,4},{4,5}}
85 139 {{1,3},{2,5},{3,5},{4,5}}
86 141 {{1,4},{1,5},{2,3},{2,4}}
87 142 {{1,4},{1,5},{2,3},{2,5}}
88 143 {{1,4},{1,5},{2,3},{3,4}}
89 144 {{1,4},{1,5},{2,3},{3,5}}
90 147 {{1,4},{1,5},{2,4},{3,4}}
91 148 {{1,4},{1,5},{2,4},{3,5}}
92 150 {{1,4},{1,5},{2,5},{3,4}}
93 151 {{1,4},{1,5},{2,5},{3,5}}
94 156 {{1,4},{2,3},{2,4},{2,5}}
95 158 {{1,4},{2,3},{2,4},{3,5}}
96 159 {{1,4},{2,3},{2,4},{4,5}}
97 160 {{1,4},{2,3},{2,5},{3,4}}
98 162 {{1,4},{2,3},{2,5},{4,5}}
99 163 {{1,4},{2,3},{3,4},{3,5}}
100 164 {{1,4},{2,3},{3,4},{4,5}}
101 165 {{1,4},{2,3},{3,5},{4,5}}
102 166 {{1,4},{2,4},{2,5},{3,4}}
103 167 {{1,4},{2,4},{2,5},{3,5}}
104 169 {{1,4},{2,4},{3,4},{3,5}}
105 170 {{1,4},{2,4},{3,4},{4,5}}
106 171 {{1,4},{2,4},{3,5},{4,5}}
107 172 {{1,4},{2,5},{3,4},{3,5}}
108 173 {{1,4},{2,5},{3,4},{4,5}}
109 174 {{1,4},{2,5},{3,5},{4,5}}
110 176 {{1,5},{2,3},{2,4},{2,5}}
111 178 {{1,5},{2,3},{2,4},{3,5}}
112 179 {{1,5},{2,3},{2,4},{4,5}}
113 180 {{1,5},{2,3},{2,5},{3,4}}
114 182 {{1,5},{2,3},{2,5},{4,5}}
115 183 {{1,5},{2,3},{3,4},{3,5}}
116 184 {{1,5},{2,3},{3,4},{4,5}}
117 185 {{1,5},{2,3},{3,5},{4,5}}
118 186 {{1,5},{2,4},{2,5},{3,4}}
119 187 {{1,5},{2,4},{2,5},{3,5}}
120 189 {{1,5},{2,4},{3,4},{3,5}}
121 190 {{1,5},{2,4},{3,4},{4,5}}
122 191 {{1,5},{2,4},{3,5},{4,5}}
123 192 {{1,5},{2,5},{3,4},{3,5}}
124 193 {{1,5},{2,5},{3,4},{4,5}}
125 194 {{1,5},{2,5},{3,5},{4,5}}

n=6全联通的方案数1296
图片文件 6岛5桥.png(前50)

6岛5桥.png

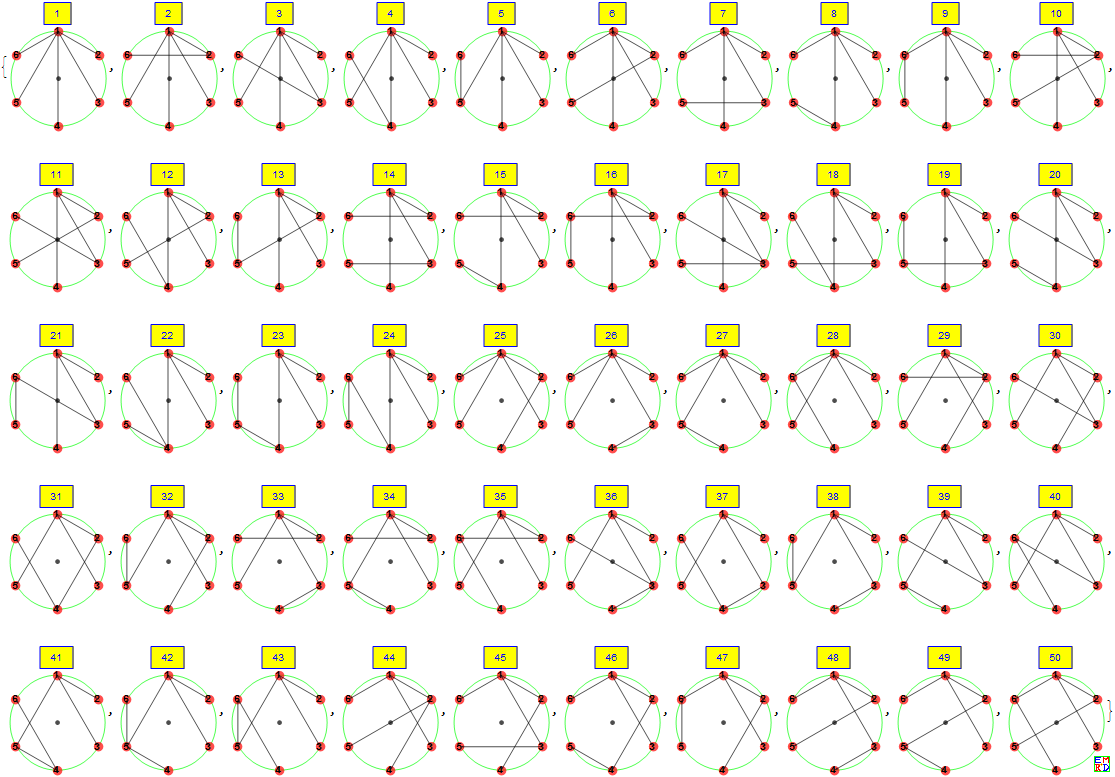
1 1 {{1,2},{1,3},{1,4},{1,5},{1,6}}
2 5 {{1,2},{1,3},{1,4},{1,5},{2,6}}
3 8 {{1,2},{1,3},{1,4},{1,5},{3,6}}
4 10 {{1,2},{1,3},{1,4},{1,5},{4,6}}
5 11 {{1,2},{1,3},{1,4},{1,5},{5,6}}
6 14 {{1,2},{1,3},{1,4},{1,6},{2,5}}
7 17 {{1,2},{1,3},{1,4},{1,6},{3,5}}
8 19 {{1,2},{1,3},{1,4},{1,6},{4,5}}
9 21 {{1,2},{1,3},{1,4},{1,6},{5,6}}
10 39 {{1,2},{1,3},{1,4},{2,5},{2,6}}
11 42 {{1,2},{1,3},{1,4},{2,5},{3,6}}
12 44 {{1,2},{1,3},{1,4},{2,5},{4,6}}
13 45 {{1,2},{1,3},{1,4},{2,5},{5,6}}
14 47 {{1,2},{1,3},{1,4},{2,6},{3,5}}
15 49 {{1,2},{1,3},{1,4},{2,6},{4,5}}
16 51 {{1,2},{1,3},{1,4},{2,6},{5,6}}
17 57 {{1,2},{1,3},{1,4},{3,5},{3,6}}
18 59 {{1,2},{1,3},{1,4},{3,5},{4,6}}
19 60 {{1,2},{1,3},{1,4},{3,5},{5,6}}
20 61 {{1,2},{1,3},{1,4},{3,6},{4,5}}
21 63 {{1,2},{1,3},{1,4},{3,6},{5,6}}
22 64 {{1,2},{1,3},{1,4},{4,5},{4,6}}
23 65 {{1,2},{1,3},{1,4},{4,5},{5,6}}
24 66 {{1,2},{1,3},{1,4},{4,6},{5,6}}
25 68 {{1,2},{1,3},{1,5},{1,6},{2,4}}
26 71 {{1,2},{1,3},{1,5},{1,6},{3,4}}
27 74 {{1,2},{1,3},{1,5},{1,6},{4,5}}
28 75 {{1,2},{1,3},{1,5},{1,6},{4,6}}
29 87 {{1,2},{1,3},{1,5},{2,4},{2,6}}
30 90 {{1,2},{1,3},{1,5},{2,4},{3,6}}
31 92 {{1,2},{1,3},{1,5},{2,4},{4,6}}
32 93 {{1,2},{1,3},{1,5},{2,4},{5,6}}
33 101 {{1,2},{1,3},{1,5},{2,6},{3,4}}
34 104 {{1,2},{1,3},{1,5},{2,6},{4,5}}
35 105 {{1,2},{1,3},{1,5},{2,6},{4,6}}
36 108 {{1,2},{1,3},{1,5},{3,4},{3,6}}
37 110 {{1,2},{1,3},{1,5},{3,4},{4,6}}
38 111 {{1,2},{1,3},{1,5},{3,4},{5,6}}
39 116 {{1,2},{1,3},{1,5},{3,6},{4,5}}
40 117 {{1,2},{1,3},{1,5},{3,6},{4,6}}
41 119 {{1,2},{1,3},{1,5},{4,5},{4,6}}
42 120 {{1,2},{1,3},{1,5},{4,5},{5,6}}
43 121 {{1,2},{1,3},{1,5},{4,6},{5,6}}
44 131 {{1,2},{1,3},{1,6},{2,4},{2,5}}
45 134 {{1,2},{1,3},{1,6},{2,4},{3,5}}
46 136 {{1,2},{1,3},{1,6},{2,4},{4,5}}
47 138 {{1,2},{1,3},{1,6},{2,4},{5,6}}
48 140 {{1,2},{1,3},{1,6},{2,5},{3,4}}
49 143 {{1,2},{1,3},{1,6},{2,5},{4,5}}
50 144 {{1,2},{1,3},{1,6},{2,5},{4,6}}
51 152 {{1,2},{1,3},{1,6},{3,4},{3,5}}
52 154 {{1,2},{1,3},{1,6},{3,4},{4,5}}
53 156 {{1,2},{1,3},{1,6},{3,4},{5,6}}
54 158 {{1,2},{1,3},{1,6},{3,5},{4,5}}
55 159 {{1,2},{1,3},{1,6},{3,5},{4,6}}
56 164 {{1,2},{1,3},{1,6},{4,5},{4,6}}
57 165 {{1,2},{1,3},{1,6},{4,5},{5,6}}
58 166 {{1,2},{1,3},{1,6},{4,6},{5,6}}
59 203 {{1,2},{1,3},{2,4},{2,5},{2,6}}
60 206 {{1,2},{1,3},{2,4},{2,5},{3,6}}
61 208 {{1,2},{1,3},{2,4},{2,5},{4,6}}
62 209 {{1,2},{1,3},{2,4},{2,5},{5,6}}
63 211 {{1,2},{1,3},{2,4},{2,6},{3,5}}
64 213 {{1,2},{1,3},{2,4},{2,6},{4,5}}
65 215 {{1,2},{1,3},{2,4},{2,6},{5,6}}
66 221 {{1,2},{1,3},{2,4},{3,5},{3,6}}
67 223 {{1,2},{1,3},{2,4},{3,5},{4,6}}
68 224 {{1,2},{1,3},{2,4},{3,5},{5,6}}
69 225 {{1,2},{1,3},{2,4},{3,6},{4,5}}
70 227 {{1,2},{1,3},{2,4},{3,6},{5,6}}
71 228 {{1,2},{1,3},{2,4},{4,5},{4,6}}
72 229 {{1,2},{1,3},{2,4},{4,5},{5,6}}
73 230 {{1,2},{1,3},{2,4},{4,6},{5,6}}
74 231 {{1,2},{1,3},{2,5},{2,6},{3,4}}
75 234 {{1,2},{1,3},{2,5},{2,6},{4,5}}
76 235 {{1,2},{1,3},{2,5},{2,6},{4,6}}
77 238 {{1,2},{1,3},{2,5},{3,4},{3,6}}
78 240 {{1,2},{1,3},{2,5},{3,4},{4,6}}
79 241 {{1,2},{1,3},{2,5},{3,4},{5,6}}
80 246 {{1,2},{1,3},{2,5},{3,6},{4,5}}
81 247 {{1,2},{1,3},{2,5},{3,6},{4,6}}
82 249 {{1,2},{1,3},{2,5},{4,5},{4,6}}
83 250 {{1,2},{1,3},{2,5},{4,5},{5,6}}
84 251 {{1,2},{1,3},{2,5},{4,6},{5,6}}
85 252 {{1,2},{1,3},{2,6},{3,4},{3,5}}
86 254 {{1,2},{1,3},{2,6},{3,4},{4,5}}
87 256 {{1,2},{1,3},{2,6},{3,4},{5,6}}
88 258 {{1,2},{1,3},{2,6},{3,5},{4,5}}
89 259 {{1,2},{1,3},{2,6},{3,5},{4,6}}
90 264 {{1,2},{1,3},{2,6},{4,5},{4,6}}
91 265 {{1,2},{1,3},{2,6},{4,5},{5,6}}
92 266 {{1,2},{1,3},{2,6},{4,6},{5,6}}
93 267 {{1,2},{1,3},{3,4},{3,5},{3,6}}
94 269 {{1,2},{1,3},{3,4},{3,5},{4,6}}
95 270 {{1,2},{1,3},{3,4},{3,5},{5,6}}
96 271 {{1,2},{1,3},{3,4},{3,6},{4,5}}
97 273 {{1,2},{1,3},{3,4},{3,6},{5,6}}
98 274 {{1,2},{1,3},{3,4},{4,5},{4,6}}
99 275 {{1,2},{1,3},{3,4},{4,5},{5,6}}
100 276 {{1,2},{1,3},{3,4},{4,6},{5,6}}
------
1290 2728 {{1,6},{2,6},{3,5},{3,6},{4,6}}
1291 2730 {{1,6},{2,6},{3,5},{4,5},{4,6}}
1292 2731 {{1,6},{2,6},{3,5},{4,5},{5,6}}
1293 2732 {{1,6},{2,6},{3,5},{4,6},{5,6}}
1294 2733 {{1,6},{2,6},{3,6},{4,5},{4,6}}
1295 2734 {{1,6},{2,6},{3,6},{4,5},{5,6}}
1296 2735 {{1,6},{2,6},{3,6},{4,6},{5,6}}

毋因群疑而阻独见　　毋任己意而废人言
毋私小惠而伤大体　　毋借公论以快私情

回复支持反对

使用道具举报

楼主| 发表于 2019-11-24 17:40:19 | 显示全部楼层

本帖最后由王守恩于 2019-11-24 17:59 编辑

dlpg070 发表于 2019-11-23 09:16
回复王守恩
用最笨方法，画图验证王守恩给出的数列是正确的
{1,3,16,125,1296}

在五座岛屿之间建造四座桥，使它们能够联通，请问有几种建桥方案？

1，给 5 个岛编上号：1，2，3，4，5；
   给10座桥编上号：12，13，14，15，23，24，25，34，35，45。
   每种建桥方案就是在这10座桥中选择合适的4座桥(8个数字)，
2，我们注意到：在满意的答案里，每个岛出现的次数肯定是相同的，
我们只要统计 “1” 出现的次数就可以了
“1”出现4个：4×1=12,13,14,15出现1次
“1”出现3个：3×4×3=12,13,14，12,13,15，12,14,15，13,14,15 各出现3次，
“1”出现2个：2×6×8=12,13，12,14，12,15，13,14，13,15，14,15 各出现8次，
“1”出现1个：1×4×16=12，13，14，15 各出现16次。
   4×1+3×4×3+2×6×8+1×4×16=200
   200×5(个岛)÷8(8个数字4座桥)=125，可以有 125 种建桥方案。

毋因群疑而阻独见　　毋任己意而废人言
毋私小惠而伤大体　　毋借公论以快私情

回复支持反对

使用道具举报

发表于 2019-11-24 19:37:57 | 显示全部楼层

王守恩发表于 2019-11-24 17:40
在五座岛屿之间建造四座桥，使它们能够联通，请问有几种建桥方案？

1，给 5 个岛编上号：1，2，3，4 ...

如何理解：
200×5(个岛)÷8(8个数字4座桥)=125，可以有 125 种建桥方案。
6岛5桥如何分析？

毋因群疑而阻独见　　毋任己意而废人言
毋私小惠而伤大体　　毋借公论以快私情

回复支持反对

使用道具举报

楼主| 发表于 2019-11-24 21:46:07 | 显示全部楼层

本帖最后由王守恩于 2019-11-25 07:44 编辑

dlpg070 发表于 2019-11-24 19:37
如何理解：
200×5(个岛)÷8(8个数字4座桥)=125，可以有 125 种建桥方案。
6岛5桥如何分析？

在六座岛屿之间建造五座桥，使它们能够联通，请问有几种建桥方案？

1，给 6 个岛编上号：1，2，3，4，5，6；
   给15座桥编上号：12，13，14，15，16，23，24，25，26，34，35，36，45，46，56。
   每种建桥方案就是在这15座桥中选择合适的5座桥(10个数字)，
2，我们注意到：在满意的答案里，每个岛出现的次数肯定是相同的，
我们只要统计 “1” 出现的次数就可以了
“1”出现5个：5×1=12,13,14,15,16出现1次
“1”出现4个：4×5×4=12,13,14,15，12,13,14,16，12,13,15,16，12,14,15,16，13,14,15,16 各出现4次，
“1”出现3个：3×10×15=12,13,14，12,13,15，12,13,16，12,14,15，12,14,16，12,15,16，13,14,15，13,14,16，13,15,16，14,15,16 各出现3次，
“1”出现2个：2×10×50=12,13，12,14，12,15，12,16，13,14，13,15，13,16，14,15，14,16，15,16 各出现50次，
“1”出现1个：1×5×125=12，13，14，15，16 各出现125次。
   5×1+4×5×4+3×10×15+2×10×50+1×5×125=2160
   2160×6(个岛)÷10(10个数字5座桥)=1296，可以有 1296 种建桥方案。
补充：
1，“1”出现4个与“1”出现1个是互补的一对；“1”出现3个与“1”出现2个是互补的一对。
2，可以这样来理解 “1”：每种方案肯定有”1“，
   5岛4桥已经有125种满意的答案，我们把 “125” 里的每个数字都+1，
   变成没有”1“的方案，......“1”×5×125=12，13，14，15，16 各出现125次，......

毋因群疑而阻独见　　毋任己意而废人言
毋私小惠而伤大体　　毋借公论以快私情

回复支持反对

使用道具举报

发表于 2019-11-27 12:42:39 | 显示全部楼层

dlpg070 发表于 2019-11-23 09:16
回复王守恩
用最笨方法，画图验证王守恩给出的数列是正确的
{1,3,16,125,1296}

代码？

点评

方法太笨，代码太丑，勉强能用，不敢贴出发表于 2019-11-27 14:13

毋因群疑而阻独见　　毋任己意而废人言
毋私小惠而伤大体　　毋借公论以快私情

回复支持反对

使用道具举报

发表于 2019-11-27 16:25:22 | 显示全部楼层

markfang2050 发表于 2019-11-27 12:42
代码？

谦虚了。思路可以说说

毋因群疑而阻独见　　毋任己意而废人言
毋私小惠而伤大体　　毋借公论以快私情

回复支持反对

使用道具举报

发表于 2019-11-28 12:48:18 | 显示全部楼层

markfang2050 发表于 2019-11-27 16:25
谦虚了。思路可以说说

盛情难却，说说解题思路，希望对你编写此题漂亮的代码有点帮助
你看到我的函数和变量命名何等丑陋，但一旦测试Ok后,我轻易不敢修改
1---解题思路:
整个解题过程分3部分
1 给出组合数对应的列表
  例如 n岛建桥的类型总数n0=Binomial[n,2]
  需要给出这n0个列表
  我用的办法：
  对岛编号 1#，---，n#
  给出相应的排列，
  选择由小到大排列的项
  例如 n=4 n0=6 得到
  tup2={{1, 2}, {1, 3}, {1, 4}, {2, 3}, {2, 4}, {3, 4}}

  对 tot=Binomial[Binomial[n,2],n-1] 亦如此
2 用剔除法(减法) 求解
  首先得到tot项的总建桥方案列表 :tup2line (包括全联通，有孤岛，2个或多个部分联通)
  分析每个方案，剔除不符合要求的方案(有孤岛或不全联通)，得到满足要求的解
  设计有2个分析函数
farr[] 返回n元素数组(各岛建桥数)---用于判别该方案是否有无桥的孤岛
isok[] 返回n元素数组(各岛联通状态 )---用于判别该方案是否全联通

3 画图演示
  演示贯穿于计算全过程，用于发现计算代码的逻辑错误和手误，已经贴出过类似代码

2---小结
n  岛数
n0=  Binomial[n,2]
tot= Binomial[Binomial[n,2],n-1] 总建桥方案数(包括全联通，有孤岛，2个或多个部分联通)
n1 去掉孤岛的建桥方案数
res  再去掉部分联通的建桥方案，即得到全联通的建桥方案数
n n0    tot n1 res
2 1       1    1    1
3 3       3    3    3
4 6       20    16 16
5 10    210 135 125
6 15    3003 1581  1296

3--- 下面是一个例子
n=4  建桥方案
n0= Binomial[4,2]=6
tup2={{1, 2}, {1, 3}, {1, 4}, {2, 3}, {2, 4}, {3, 4}}
tot= Binomial[Binomial[4,2],4-1]= 20 总建桥方案数

line 一个建桥方案  例如: {{1,2},{1,3},{1,4}}  数字代表岛的编号，{1,2}表示1#岛和2#岛之间的桥，从小到大排序
arr n个元素的数组  例如: {True,{3,1,1,1}}  数组表示各岛的桥头数(0,1,2---,n-1),各元素之和 2(n-1),前部的True
               表示元素值没有0，即没有无桥的孤岛
r n个元素的数组  例如: {4,{1,1,1,1}}  数组表示各岛联通情况，1--- 联通， 0---不联通 (1,2---,n-1),
               各元素都是1，表示全联通,即前部的数字=n
含分析的中间结果
注意 2,6,13,20 *不满足要求
1 1 {1,{{1,2},{1,3},{1,4}},{True,{3,1,1,1}},{4,{1,1,1,1}}}
2 2 {2,{{1,2},{1,3},{2,3}},{False,{2,2,2,0}},{3,{1,1,1,0}}} *不满足要求
3 3 {3,{{1,2},{1,3},{2,4}},{True,{2,2,1,1}},{4,{1,1,1,1}}}
4 4 {4,{{1,2},{1,3},{3,4}},{True,{2,1,2,1}},{4,{1,1,1,1}}}
5 5 {5,{{1,2},{1,4},{2,3}},{True,{2,2,1,1}},{4,{1,1,1,1}}}
6 6 {6,{{1,2},{1,4},{2,4}},{False,{2,2,0,2}},{3,{1,1,0,1}}} *不满足要求
7 7 {7,{{1,2},{1,4},{3,4}},{True,{2,1,1,2}},{4,{1,1,1,1}}}
8 8 {8,{{1,2},{2,3},{2,4}},{True,{1,3,1,1}},{4,{1,1,1,1}}}
9 9 {9,{{1,2},{2,3},{3,4}},{True,{1,2,2,1}},{4,{1,1,1,1}}}
10 10 {10,{{1,2},{2,4},{3,4}},{True,{1,2,1,2}},{4,{1,1,1,1}}}
11 11 {11,{{1,3},{1,4},{2,3}},{True,{2,1,2,1}},{4,{1,1,1,1}}}
12 12 {12,{{1,3},{1,4},{2,4}},{True,{2,1,1,2}},{4,{1,1,1,1}}}
13 13 {13,{{1,3},{1,4},{3,4}},{False,{2,0,2,2}},{3,{1,0,1,1}}} *不满足要求
14 14 {14,{{1,3},{2,3},{2,4}},{True,{1,2,2,1}},{4,{1,1,1,1}}}
15 15 {15,{{1,3},{2,3},{3,4}},{True,{1,1,3,1}},{4,{1,1,1,1}}}
16 16 {16,{{1,3},{2,4},{3,4}},{True,{1,1,2,2}},{4,{1,1,1,1}}}
17 17 {17,{{1,4},{2,3},{2,4}},{True,{1,2,1,2}},{4,{1,1,1,1}}}
18 18 {18,{{1,4},{2,3},{3,4}},{True,{1,1,2,2}},{4,{1,1,1,1}}}
19 19 {19,{{1,4},{2,4},{3,4}},{True,{1,1,1,3}},{4,{1,1,1,1}}}
20 20 {20,{{2,3},{2,4},{3,4}},{False,{0,2,2,2}},{3,{0,1,1,1}}} *不满足要求

含不满足要求的中间结果对应图形
4岛3桥tmp.png

4岛3桥tmp.png

根据中间结果，很容易得到正确结果！！！

注意 2,6,13,20 *不满足要求

4---改进的设想(直接生成（加法)建桥方案)
正在进行，速度快些，存储空间少很多，算法麻烦些，希望找到通项，类似王守恩的方法

毋因群疑而阻独见　　毋任己意而废人言
毋私小惠而伤大体　　毋借公论以快私情

回复支持反对

使用道具举报

12 3 4 / 4 页下一页

返回列表发新帖

小黑屋|手机版|数学研发网 ( 苏ICP备07505100号 )

GMT+8, 2024-12-21 23:44 , Processed in 0.028259 second(s), 20 queries .

Powered by Discuz! X3.5

© 2001-2024 Discuz! Team.

快速回复 返回顶部 返回列表