以三角形ABC各边顶点为焦点作过内心的椭圆，三椭圆在三角形外的交点为XYZ

chyanog

如图所示，以三角形ABC各边顶点为焦点作过内心的椭圆，三椭圆在三角形外的交点分别为XYZ，求证AX、BY、CZ三线共点或平行。

creasson

有趣的结论

hujunhua

确实是个有趣的结论。

这得有一个基础：共一个焦点的俩椭圆最多只有两个交点。这得证明一下！

把椭圆换成双曲线，基础就不复存在，三线共点的结论也不再成立。

mathe

通过极坐标可证共一个焦点的俩椭圆最多只有两个交点

chyanog

类似问题
Two theorems on the focus-sharing ellipses
http://jcgeometry.org/Articles/Volume1/JCG2012V1pp1-5.pdf

The Love for the Three Conics
http://forumgeom.fau.edu/FG2018volume18/FG201848.pdf

creasson

我尝试了求各点坐标，然而mathematica无法给出最终结果。令
\[ \mathop {BA}\limits^ \to  {\rm{ = }}\frac{{\left( {s + t} \right)\left( {1 - st} \right)}}{{s{{\left( {1 - it} \right)}^2}}}\mathop {BC}\limits^ \to  \]
\[ \mathop {BY} \limits^ \to  {\rm{ = }}\frac{{{{\left( {1 + p + ipu} \right)}^2}}}{{1 + p + p{u^2}}}\mathop {BC}\limits^ \to  \]
参数$p,u$ 是如下方程组的解
$ eq1: = 4 p^4 t^4+8 p^4 t^2+4 p^4+8 p^3 t^4+16 p^3 t^2+8 p^3-4 p^2 s^2 t^4-4 p^2 s^2 t^2+4 p^2 s t^3+4 p^2 s t+4 p^2 t^4+8 p^2 t^2+4 p^2-4 p s^2 t^4-4 p s^2 t^2+4 p s t^3+4 p s t-s^2 t^4+2 s t^3-t^2 = 0  $
$ eq2: = 4 q^4 s^2+8 q^4 s t+4 q^4 t^2+8 q^3 s^2+16 q^3 s t+8 q^3 t^2-4 q^2 s^2 t^2+4 q^2 s^2+12 q^2 s t+4 q^2 t^2-4 q s^2 t^2+4 q s t-s^2 t^2 $
$ eq3: = p^2 q s t^2 u^2+p^2 q s t^2+p^2 q s u^2+p^2 q s+p^2 s t^2-2 p^2 s t u+p^2 s u^2+p q^2 s^2 t u^2+p q^2 s^2 t+p q^2 s t^2 u^2+p q^2 s t^2-p q^2 s u^2-p q^2 s-p q^2 t u^2-p q^2 t+p q s^2 t u^2+p q s^2 t+p q s t^2 u^2+3 p q s t^2-p q s u^2+p q s-p q t u^2-p q t+2 p s t^2-2 p s t u+q^2 s^2 t+q^2 s t^2-q^2 s-q^2 t+q s^2 t+2 q s t^2-q t+s t^2 $

mathematica求解：
$ \text{FullSimplify}[\text{Solve}[\{\text{eq1}=0,\text{eq2}=0,\text{eq3}=0,p>0,q>0,s>0,t>0,s t<1,u\in \mathbb{R}\},\{p,q,u\}]] $
$ \text{FullSimplify}[\text{Reduce}[\{\text{eq1}=0 \land \text{eq2}=0\land \text{eq3}=0\land p>0\land q>0\land s>0\land t>0\land s t<1\land u\in \mathbb{R}\},\{u,p,q\}]] $
两组解，其中一组解是内心的。

例如：
$ s\to \frac{1}{\sqrt{3}},t\to \frac{1}{\sqrt{3}}  $ 时，$ p\to \frac{1}{\sqrt{3}}-\frac{1}{2},q\to \frac{1}{\sqrt{3}}-\frac{1}{2},u\to -15 \sqrt{3}-26 $
$ s\to \frac{1}{2},t\to \frac{1}{\sqrt{3}} $ 时，$ p\to \frac{1}{8} \left(2 \sqrt{3}+\sqrt{5}-5\right),q\to \sqrt{5}-\frac{1}{2} \sqrt{3 \left(4 \sqrt{5}+9\right)}+\frac{3}{2},u\to \frac{1}{11} \left(-135 \sqrt{3}-109 \sqrt{5}-64 \sqrt{15}-227\right) $

我感觉$Y$点横纵坐标分别可用一个系数为$s,t$的多项式、次数不高于4的方程表示出来，然而没有计算出来。

chyanog

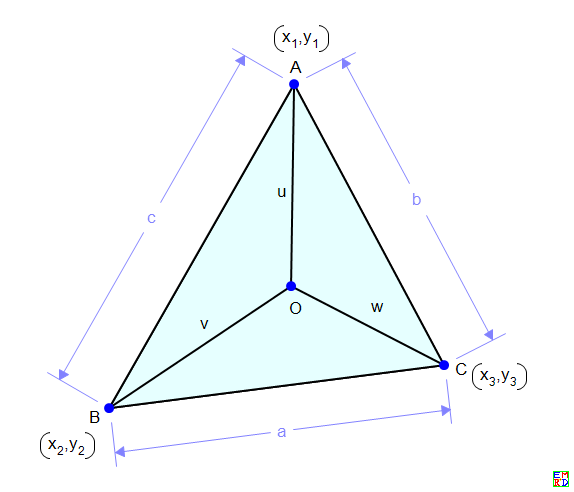
如图所示，O是△ABC的内心，令
$u=\sqrt{\frac{b c (-a+b+c)}{a+b+c}},v=\sqrt{\frac{a c (a-b+c)}{a+b+c}},w=\sqrt{\frac{a b (a+b-c)}{a+b+c}}$
$S=2 \left(x_1 \left(y_2-y_3\right)+x_2 \left(y_3-y_1\right)+x_3 \left(y_1-y_2\right)\right)$
$T=2 \text{sgn}(S) \sqrt{\left(a^2-(v-w)^2\right) \left((u+w)^2-b^2\right) \left((u+v)^2-c^2\right)}$
$\S_1=S \left(a^2-(v-w)^2\right) \left(a^2-b^2-c^2+2 (u+v) (u+w)\right)+T \left(a^2 (2 u+v+w)+b^2 (v-w)+c^2 (w-v)\right)$
$S_2=S \left((u+w)^2-b^2\right) \left(a^2-b^2+c^2-2 (u+v) (v-w)\right)+T \left(-a^2 (u+w)+b^2 (-u-2 v+w)+c^2 (u+w)\right)$
$S_3=S \left((u+v)^2-c^2\right) \left(a^2+b^2-c^2+2 (v-w) (u+w)\right)+T \left(-a^2 (u+v)+b^2 (u+v)+c^2 (-u+v-2 w)\right)$
则X点的坐标可以表示为：
$  ( \frac{S_1 x_1+S_2 x_2+S_3 x_3}{S_1+S_2+S_3},\frac{S_1 y_1+S_2 y_2+S_3 y_3}{S_1+S_2+S_3} ) $
轮换可得YZ的坐标。上面的式子具有一定几何意义，S表示△ABC有向面积的4倍，$S_1:S_2:S_3\text{=}S_{\text{△XBC}}:S_{\text{△XCA}}:S_{\text{△XAB}}$，T的含义还不清楚，使用几何意义说不定可以进一步简化。
Mathematica检验代码：

1. Clear["`*"];
   
2. ellipse[F1_, F2_, P_] :=
   
3.   With[{ff = Norm[F1 - F2], p = Norm[P - F1], q = Norm[P - F2]},
   
4.    Rotate[Circle[(F1 + F2)/2, {(p + q)/2 , Sqrt[(p + q)^2 - ff^2]/2 }], ArcTan @@ (F1 - F2)]];
   
5. 
   
6. intersectionPoint[A : {x1_, y1_}, B : {x2_, y2_}, C : {x3_, y3_}] :=
   
7.   Module[{a, b, c, u, v, w, S1, S2, S3, S, T},
   
8.    {a, b, c} = {Norm[B - C], Norm[C - A], Norm[A - B]};
   
9.    {u, v, w} = {Sqrt[(b c (-a + b + c))/(a + b + c)], Sqrt[( a c (a - b + c))/(a + b + c)], Sqrt[(a b (a + b - c))/( a + b + c)]};
   
10.    S = 2 (x3 (y1 - y2) + x1 (y2 - y3) + x2 (-y1 + y3));
    
11.    T = 2 Sign[S] Sqrt[((u + v)^2 - c^2) (a^2 - (v - w)^2) ((u + w)^2 - b^2)];
    
12.    S1 = S (a^2 - (v - w)^2) (a^2 - b^2 - c^2 + 2 (u + v) (u + w)) + T (a^2 (2 u + v + w) + b^2 (v - w) + c^2 (-v + w));
    
13.    S2 = S (-b^2 + (u + w)^2) (a^2 - b^2 + c^2 - 2 (u + v) (v - w)) +  T (-a^2 (u + w) + c^2 (u + w) + b^2 (-u - 2 v + w));
    
14.    S3 = S (-c^2 + (u + v)^2) (a^2 + b^2 - c^2 + 2 (v - w) (u + w)) + T (-a^2 (u + v) + b^2 (u + v) + c^2 (-u + v - 2 w));
    
15.    {S1 x1 + S2 x2 + S3 x3, S1 y1 + S2 y2 + S3 y3}/(S1 + S2 + S3)
    
16.    ];
    
17. 
    
18. Manipulate[
    
19. Module[{A1, B1, C1, O1, X, Y, Z, eq1, eq2, eq3},
    
20.   {B1, C1, A1} = pt; O1 = First@Insphere[pt];
    
21.   {Y, Z, X} = intersectionPoint @@@ {{B1, C1, A1}, {C1, A1, B1}, {A1, B1, C1}};
    
22.   Graphics[{{EdgeForm[Black], Opacity[0.05], Polygon[pt]},
    
23.     PointSize[Large], Point[O1], Point[{X, Y, Z}],
    
24.     {Orange, ellipse @@@ {{A1, B1, O1}, {B1, C1, O1}, {C1, A1, O1}}},
    
25.     {Blue, InfiniteLine /@ {{A1, X}, {B1, Y}, {C1, Z}}},
    
26.     {Red, RegionIntersection[InfiniteLine /@ {{A1, X}, {B1, Y}}]},
    
27.     {MapThread[{Blue, Disk[#1, 0.28],  Text[Style[#2, White], #1]} &, {{A1, B1, C1}, {"A", "B",  "C"} }],
    
28.      MapThread[{RGBColor[{0, 0.5, 1}], Disk[#1, 0.28], Text[Style[#2, White], #1]} &, {{O1, X, Y, Z}, {"O", "X", "Y", "Z"} }]}
    
29.     }, PlotRange -> 10, ImageSize -> 720, BaseStyle -> 14, Axes -> 0
    
30.    ]
    
31.   ], {{pt, N@{{-5, -5}, {6, -4}, {0, 3.5}}}, Locator, Appearance -> ""}, TrackedSymbols :> {pt}
    
32. ]

复制代码

creasson

重新计算，得到了这样的结果：
\[\mathop {BA}\limits^ \to  {\rm{ = }}\frac{{\left( {s + t} \right)\left( {1 - st} \right)}}{{s{{\left( {1 - it} \right)}^2}}}\mathop {BC}\limits^ \to  \]
\[\mathop {BY}\limits^ \to  {\rm{ = }}\left( {x + yi} \right)\mathop {BC}\limits^ \to  \]
其中 $x,y$分别满足方程:
$$-7 s^8 x^4 t^{16}-36 s^6 x^4 t^{16}-50 s^4 x^4 t^{16}-20 s^2 x^4 t^{16}+x^4 t^{16}+32 s^8 x^3 t^{16}+96 s^6 x^3 t^{16}+96 s^4 x^3 t^{16}+32 s^2 x^3 t^{16}-16 s^8 x^2 t^{16}-48 s^6 x^2 t^{16}-48 s^4 x^2 t^{16}-16 s^2 x^2 t^{16}-8 s^7 x^4 t^{15}+8 s^5 x^4 t^{15}+40 s^3 x^4 t^{15}+24 s x^4 t^{15}+36 s^9 x^3 t^{15}+64 s^7 x^3 t^{15}-24 s^5 x^3 t^{15}-96 s^3 x^3 t^{15}-44 s x^3 t^{15}-80 s^9 x^2 t^{15}-208 s^7 x^2 t^{15}-144 s^5 x^2 t^{15}+16 s^3 x^2 t^{15}+32 s x^2 t^{15}+32 s^9 x t^{15}+96 s^7 x t^{15}+96 s^5 x t^{15}+32 s^3 x t^{15}+48 s^{10} t^{14}+80 s^8 t^{14}+16 s^6 t^{14}-16 s^4 t^{14}-64 s^8 x^4 t^{14}-264 s^6 x^4 t^{14}-240 s^4 x^4 t^{14}-40 s^2 x^4 t^{14}+236 s^8 x^3 t^{14}+592 s^6 x^3 t^{14}+360 s^4 x^3 t^{14}+16 s^2 x^3 t^{14}+12 x^3 t^{14}-26 s^{10} x^2 t^{14}-184 s^8 x^2 t^{14}-188 s^6 x^2 t^{14}+120 s^4 x^2 t^{14}+134 s^2 x^2 t^{14}-16 x^2 t^{14}-64 s^{10} x t^{14}-32 s^8 x t^{14}+32 s^6 x t^{14}-96 s^4 x t^{14}-96 s^2 x t^{14}+48 s^{11} t^{13}-176 s^9 t^{13}-432 s^7 t^{13}-144 s^5 t^{13}-24 s^7 x^4 t^{13}+296 s^5 x^4 t^{13}+376 s^3 x^4 t^{13}+56 s x^4 t^{13}+64 s^3 t^{13}+252 s^9 x^3 t^{13}+64 s^7 x^3 t^{13}-968 s^5 x^3 t^{13}-800 s^3 x^3 t^{13}-20 s x^3 t^{13}-508 s^9 x^2 t^{13}-368 s^7 x^2 t^{13}+728 s^5 x^2 t^{13}+464 s^3 x^2 t^{13}-124 s x^2 t^{13}-60 s^{11} x t^{13}+640 s^9 x t^{13}+840 s^7 x t^{13}-256 s^5 x t^{13}-300 s^3 x t^{13}+96 s x t^{13}+9 s^{12} t^{12}-164 s^{10} t^{12}+206 s^8 t^{12}+908 s^6 t^{12}+433 s^4 t^{12}-236 s^8 x^4 t^{12}-736 s^6 x^4 t^{12}-592 s^4 x^4 t^{12}-112 s^2 x^4 t^{12}-4 x^4 t^{12}+324 s^8 x^3 t^{12}+1328 s^6 x^3 t^{12}+1304 s^4 x^3 t^{12}+304 s^2 x^3 t^{12}+4 x^3 t^{12}-96 s^2 t^{12}-156 s^{10} x^2 t^{12}+758 s^8 x^2 t^{12}+816 s^6 x^2 t^{12}-540 s^4 x^2 t^{12}-420 s^2 x^2 t^{12}+22 x^2 t^{12}+356 s^{10} x t^{12}-1392 s^8 x t^{12}-2632 s^6 x t^{12}-336 s^4 x t^{12}+516 s^2 x t^{12}-32 x t^{12}+20 s^{11} t^{11}+120 s^9 t^{11}-112 s^7 t^{11}-888 s^5 t^{11}+24 s^7 x^4 t^{11}+1320 s^5 x^4 t^{11}+1224 s^3 x^4 t^{11}-8 s x^4 t^{11}-612 s^3 t^{11}+596 s^9 x^3 t^{11}-96 s^7 x^3 t^{11}-3224 s^5 x^3 t^{11}-2496 s^3 x^3 t^{11}+100 s x^3 t^{11}-264 s^9 x^2 t^{11}-1136 s^7 x^2 t^{11}+224 s^5 x^2 t^{11}+1072 s^3 x^2 t^{11}-24 s x^2 t^{11}+64 s t^{11}-76 s^{11} x t^{11}-372 s^9 x t^{11}+1640 s^7 x t^{11}+2904 s^5 x t^{11}+740 s^3 x t^{11}-228 s x t^{11}+12 s^{12} t^{10}-258 s^{10} t^{10}+160 s^8 t^{10}+300 s^6 t^{10}+324 s^4 t^{10}-464 s^8 x^4 t^{10}-984 s^6 x^4 t^{10}-1120 s^4 x^4 t^{10}-568 s^2 x^4 t^{10}-292 s^8 x^3 t^{10}+1584 s^6 x^3 t^{10}+3048 s^4 x^3 t^{10}+1456 s^2 x^3 t^{10}-36 x^3 t^{10}+438 s^2 t^{10}-102 s^{10} x^2 t^{10}+956 s^8 x^2 t^{10}+1612 s^6 x^2 t^{10}-768 s^4 x^2 t^{10}-1174 s^2 x^2 t^{10}+52 x^2 t^{10}+548 s^{10} x t^{10}-676 s^8 x t^{10}-2776 s^6 x t^{10}-1704 s^4 x t^{10}-140 s^2 x t^{10}+12 x t^{10}-16 t^{10}-72 s^{11} t^9+628 s^9 t^9-184 s^7 t^9-672 s^5 t^9+200 s^7 x^4 t^9+2440 s^5 x^4 t^9+1944 s^3 x^4 t^9-104 s x^4 t^9+64 s^3 t^9+588 s^9 x^3 t^9+288 s^7 x^3 t^9-4744 s^5 x^3 t^9-3968 s^3 x^3 t^9+28 s x^3 t^9+108 s^9 x^2 t^9-976 s^7 x^2 t^9-952 s^5 x^2 t^9+1072 s^3 x^2 t^9+364 s x^2 t^9-148 s t^9+8 s^{11} x t^9-1668 s^9 x t^9+1008 s^7 x t^9+3992 s^5 x t^9+1192 s^3 x t^9-180 s x t^9-2 s^{12} t^8+128 s^{10} t^8-619 s^8 t^8-172 s^6 t^8+532 s^4 t^8-530 s^8 x^4 t^8-600 s^6 x^4 t^8-1604 s^4 x^4 t^8-1256 s^2 x^4 t^8+6 x^4 t^8-812 s^8 x^3 t^8+912 s^6 x^3 t^8+3928 s^4 x^3 t^8+2512 s^2 x^3 t^8-12 x^3 t^8-44 s^2 t^8+120 s^{10} x^2 t^8+42 s^8 x^2 t^8-552 s^6 x^2 t^8+76 s^4 x^2 t^8-736 s^2 x^2 t^8-38 x^2 t^8-120 s^{10} x t^8+2188 s^8 x t^8+192 s^6 x t^8-2520 s^4 x t^8-808 s^2 x t^8+44 x t^8+17 t^8-16 s^{11} t^7-8 s^9 t^7+144 s^7 t^7+288 s^5 t^7+360 s^7 x^4 t^7+2200 s^5 x^4 t^7+1656 s^3 x^4 t^7-56 s x^4 t^7+172 s^9 x^3 t^7+1024 s^7 x^3 t^7-4040 s^5 x^3 t^7-3552 s^3 x^3 t^7-68 s x^3 t^7-448 s^9 x^2 t^7-112 s^7 x^2 t^7+1968 s^5 x^2 t^7+944 s^3 x^2 t^7+80 s x^2 t^7-24 s t^7+8 s^{11} x t^7+88 s^9 x t^7-1488 s^7 x t^7-112 s^5 x t^7+392 s^3 x t^7+216 s x t^7-4 s^{12} t^6+108 s^{10} t^6-268 s^8 t^6+232 s^6 t^6-60 s^4 t^6-352 s^8 x^4 t^6-56 s^6 x^4 t^6-1456 s^4 x^4 t^6-1304 s^2 x^4 t^6-316 s^8 x^3 t^6-336 s^6 x^3 t^6+3128 s^4 x^3 t^6+2288 s^2 x^3 t^6+36 x^3 t^6-212 s^2 t^6+58 s^{10} x^2 t^6+816 s^8 x^2 t^6-1284 s^6 x^2 t^6-1192 s^4 x^2 t^6-550 s^2 x^2 t^6-56 x^2 t^6-152 s^{10} x t^6+312 s^8 x t^6+1456 s^6 x t^6-752 s^4 x t^6+40 s^2 x t^6-8 x t^6+12 t^6+24 s^{11} t^5-256 s^9 t^5+464 s^7 t^5-288 s^5 t^5+312 s^7 x^4 t^5+888 s^5 x^4 t^5+744 s^3 x^4 t^5+40 s x^4 t^5-40 s^3 t^5-76 s^9 x^3 t^5+768 s^7 x^3 t^5-1880 s^5 x^3 t^5-1824 s^3 x^3 t^5+4 s x^3 t^5-228 s^9 x^2 t^5-1104 s^7 x^2 t^5+2920 s^5 x^2 t^5+880 s^3 x^2 t^5-228 s x^2 t^5+96 s t^5-12 s^{11} x t^5+568 s^9 x t^5-536 s^7 x t^5-1680 s^5 x t^5+388 s^3 x t^5+56 s x t^5+s^{12} t^4-60 s^{10} t^4+340 s^8 t^4-476 s^6 t^4+237 s^4 t^4-124 s^8 x^4 t^4+96 s^6 x^4 t^4-704 s^4 x^4 t^4-656 s^2 x^4 t^4-4 x^4 t^4+204 s^8 x^3 t^4-816 s^6 x^3 t^4+1608 s^4 x^3 t^4+1232 s^2 x^3 t^4+12 x^3 t^4-16 s^2 t^4-28 s^{10} x^2 t^4+554 s^8 x^2 t^4+640 s^6 x^2 t^4-1892 s^4 x^2 t^4-596 s^2 x^2 t^4+10 x^2 t^4+84 s^{10} x t^4-984 s^8 x t^4+568 s^6 x t^4+768 s^4 x t^4+20 s^2 x t^4-8 x t^4-10 t^4-4 s^{11} t^3+80 s^9 t^3-288 s^7 t^3+344 s^5 t^3+136 s^7 x^4 t^3+56 s^5 x^4 t^3+152 s^3 x^4 t^3+40 s x^4 t^3-156 s^3 t^3-36 s^9 x^3 t^3+32 s^7 x^3 t^3-136 s^5 x^3 t^3-512 s^3 x^3 t^3+12 s x^3 t^3+152 s^9 x^2 t^3-848 s^7 x^2 t^3+384 s^5 x^2 t^3+528 s^3 x^2 t^3-88 s x^2 t^3+24 s t^3+4 s^{11} x t^3-196 s^9 x t^3+968 s^7 x t^3-648 s^5 x t^3-12 s^3 x t^3+12 s x t^3+6 s^{10} t^2-60 s^8 t^2+156 s^6 t^2-160 s^4 t^2-16 s^8 x^4 t^2+24 s^6 x^4 t^2-128 s^4 x^4 t^2-136 s^2 x^4 t^2+116 s^8 x^3 t^2-304 s^6 x^3 t^2+376 s^4 x^3 t^2+336 s^2 x^3 t^2-12 x^3 t^2+62 s^2 t^2+6 s^{10} x^2 t^2-244 s^8 x^2 t^2+692 s^6 x^2 t^2-528 s^4 x^2 t^2-202 s^2 x^2 t^2+20 x^2 t^2-12 s^{10} x t^2+204 s^8 x t^2-568 s^6 x t^2+440 s^4 x t^2-60 s^2 x t^2-4 x t^2-4 t^2-4 s^9 t+24 s^7 t-48 s^5 t+24 s^7 x^4 t-40 s^5 x^4 t+8 s^3 x^4 t+8 s x^4 t+40 s^3 t+4 s^9 x^3 t-96 s^7 x^3 t+168 s^5 x^3 t-64 s^3 x^3 t-12 s x^3 t-12 s^9 x^2 t+144 s^7 x^2 t-264 s^5 x^2 t+144 s^3 x^2 t-12 s x^2 t-12 s t+12 s^9 x t-96 s^7 x t+184 s^5 x t-128 s^3 x t+28 s x t+s^8-4 s^6+6 s^4+s^8 x^4-4 s^6 x^4+6 s^4 x^4-4 s^2 x^4+x^4-4 s^8 x^3+16 s^6 x^3-24 s^4 x^3+16 s^2 x^3-4 x^3-4 s^2+6 s^8 x^2-24 s^6 x^2+36 s^4 x^2-24 s^2 x^2+6 x^2-4 s^8 x+16 s^6 x-24 s^4 x+16 s^2 x-4 x+1=0$$

$$s^{12} t^{16}-4 s^{10} t^{16}-2 s^8 t^{16}+12 s^6 t^{16}+9 s^4 t^{16}-7 s^8 y^4 t^{16}-36 s^6 y^4 t^{16}-50 s^4 y^4 t^{16}-20 s^2 y^4 t^{16}+y^4 t^{16}+20 s^9 y^3 t^{16}+64 s^7 y^3 t^{16}+72 s^5 y^3 t^{16}+32 s^3 y^3 t^{16}+4 s y^3 t^{16}-18 s^{10} y^2 t^{16}-24 s^8 y^2 t^{16}+4 s^6 y^2 t^{16}+8 s^4 y^2 t^{16}-2 s^2 y^2 t^{16}+4 s^{11} y t^{16}-24 s^7 y t^{16}-32 s^5 y t^{16}-12 s^3 y t^{16}-12 s^{11} t^{15}+24 s^9 t^{15}+48 s^7 t^{15}-24 s^5 t^{15}-8 s^7 y^4 t^{15}+8 s^5 y^4 t^{15}+40 s^3 y^4 t^{15}+24 s y^4 t^{15}-36 s^3 t^{15}-68 s^8 y^3 t^{15}-208 s^6 y^3 t^{15}-216 s^4 y^3 t^{15}-80 s^2 y^3 t^{15}-4 y^3 t^{15}+148 s^9 y^2 t^{15}+320 s^7 y^2 t^{15}+200 s^5 y^2 t^{15}+32 s^3 y^2 t^{15}+4 s y^2 t^{15}-60 s^{10} y t^{15}-144 s^8 y t^{15}-72 s^6 y t^{15}+48 s^4 y t^{15}+36 s^2 y t^{15}-4 s^{12} t^{14}+46 s^{10} t^{14}-64 s^8 t^{14}-196 s^6 t^{14}-28 s^4 t^{14}-64 s^8 y^4 t^{14}-264 s^6 y^4 t^{14}-240 s^4 y^4 t^{14}-40 s^2 y^4 t^{14}+92 s^9 y^3 t^{14}+256 s^7 y^3 t^{14}+504 s^5 y^3 t^{14}+416 s^3 y^3 t^{14}+76 s y^3 t^{14}+54 s^2 t^{14}+4 s^{10} y^2 t^{14}-210 s^8 y^2 t^{14}-544 s^6 y^2 t^{14}-508 s^4 y^2 t^{14}-180 s^2 y^2 t^{14}-2 y^2 t^{14}-28 s^{11} y t^{14}+172 s^9 y t^{14}+488 s^7 y t^{14}+376 s^5 y t^{14}+52 s^3 y t^{14}-36 s y t^{14}+24 s^{11} t^{13}-140 s^9 t^{13}+56 s^7 t^{13}+368 s^5 t^{13}-24 s^7 y^4 t^{13}+296 s^5 y^4 t^{13}+376 s^3 y^4 t^{13}+56 s y^4 t^{13}+112 s^3 t^{13}-572 s^8 y^3 t^{13}-944 s^6 y^3 t^{13}-840 s^4 y^3 t^{13}-496 s^2 y^3 t^{13}-28 y^3 t^{13}+360 s^9 y^2 t^{13}+736 s^7 y^2 t^{13}+560 s^5 y^2 t^{13}+416 s^3 y^2 t^{13}+232 s y^2 t^{13}-36 s t^{13}+212 s^{10} y t^{13}-260 s^8 y t^{13}-792 s^6 y t^{13}-456 s^4 y t^{13}-124 s^2 y t^{13}+12 y t^{13}-2 s^{12} t^{12}-64 s^{10} t^{12}+333 s^8 t^{12}+84 s^6 t^{12}-412 s^4 t^{12}-236 s^8 y^4 t^{12}-736 s^6 y^4 t^{12}-592 s^4 y^4 t^{12}-112 s^2 y^4 t^{12}-4 y^4 t^{12}+36 s^9 y^3 t^{12}+864 s^7 y^3 t^{12}+2056 s^5 y^3 t^{12}+1408 s^3 y^3 t^{12}+244 s y^3 t^{12}-108 s^2 t^{12}+194 s^{10} y^2 t^{12}-1092 s^8 y^2 t^{12}-1972 s^6 y^2 t^{12}-1072 s^4 y^2 t^{12}-382 s^2 y^2 t^{12}-92 y^2 t^{12}+8 s^{11} y t^{12}-628 s^9 y t^{12}+464 s^7 y t^{12}+1176 s^5 y t^{12}+200 s^3 y t^{12}+60 s y t^{12}+9 t^{12}+48 s^{11} t^{11}+56 s^9 t^{11}-624 s^7 t^{11}-224 s^5 t^{11}+24 s^7 y^4 t^{11}+1320 s^5 y^4 t^{11}+1224 s^3 y^4 t^{11}-8 s y^4 t^{11}+320 s^3 t^{11}-1332 s^8 y^3 t^{11}-1456 s^6 y^3 t^{11}-2072 s^4 y^3 t^{11}-1648 s^2 y^3 t^{11}-20 y^3 t^{11}-804 s^9 y^2 t^{11}+1440 s^7 y^2 t^{11}+2360 s^5 y^2 t^{11}+1216 s^3 y^2 t^{11}+524 s y^2 t^{11}+40 s t^{11}+264 s^{10} y t^{11}+1500 s^8 y t^{11}-704 s^6 y t^{11}-1528 s^4 y t^{11}-40 s^2 y t^{11}-4 y t^{11}+12 s^{12} t^{10}-196 s^{10} t^{10}+84 s^8 t^{10}+1080 s^6 t^{10}+164 s^4 t^{10}-464 s^8 y^4 t^{10}-984 s^6 y^4 t^{10}-1120 s^4 y^4 t^{10}-568 s^2 y^4 t^{10}-372 s^9 y^3 t^{10}+2144 s^7 y^3 t^{10}+3512 s^5 y^3 t^{10}+2112 s^3 y^3 t^{10}+668 s y^3 t^{10}-180 s^2 t^{10}+120 s^{10} y^2 t^{10}+770 s^8 y^2 t^{10}-1816 s^6 y^2 t^{10}-1780 s^4 y^2 t^{10}-816 s^2 y^2 t^{10}-254 y^2 t^{10}+104 s^{11} y t^{10}-1096 s^9 y t^{10}-2992 s^7 y t^{10}+624 s^5 y t^{10}+1160 s^3 y t^{10}+24 s y t^{10}-4 t^{10}-24 s^{11} t^9+368 s^9 t^9-224 s^7 t^9-1584 s^5 t^9+200 s^7 y^4 t^9+2440 s^5 y^4 t^9+1944 s^3 y^4 t^9-104 s y^4 t^9-8 s^3 t^9-972 s^8 y^3 t^9-1168 s^6 y^3 t^9-3272 s^4 y^3 t^9-2704 s^2 y^3 t^9+52 y^3 t^9-1552 s^9 y^2 t^9-256 s^7 y^2 t^9+2528 s^5 y^2 t^9+1152 s^3 y^2 t^9+688 s y^2 t^9+64 s t^9-312 s^{10} y t^9+1944 s^8 y t^9+3984 s^6 y t^9-464 s^4 y t^9-408 s^2 y t^9-8 y t^9+9 s^{12} t^8-28 s^{10} t^8-412 s^8 t^8+164 s^6 t^8+1621 s^4 t^8-530 s^8 y^4 t^8-600 s^6 y^4 t^8-1604 s^4 y^4 t^8-1256 s^2 y^4 t^8+6 y^4 t^8-708 s^9 y^3 t^8+2688 s^7 y^3 t^8+2264 s^5 y^3 t^8+1568 s^3 y^3 t^8+1292 s y^3 t^8-48 s^2 t^8-238 s^{10} y^2 t^8+3536 s^8 y^2 t^8+956 s^6 y^2 t^8-1912 s^4 y^2 t^8-766 s^2 y^2 t^8-328 y^2 t^8+52 s^{11} y t^8+216 s^9 y t^8-2616 s^7 y t^8-3376 s^5 y t^8+356 s^3 y t^8+56 s y t^8-10 t^8-36 s^{11} t^7+112 s^9 t^7+320 s^7 t^7-8 s^5 t^7+360 s^7 y^4 t^7+2200 s^5 y^4 t^7+1656 s^3 y^4 t^7-56 s y^4 t^7-1052 s^3 t^7+372 s^8 y^3 t^7-1072 s^6 y^3 t^7-2568 s^4 y^3 t^7-1968 s^2 y^3 t^7+52 y^3 t^7+12 s^9 y^2 t^7-3264 s^7 y^2 t^7-968 s^5 y^2 t^7+224 s^3 y^2 t^7+604 s y^2 t^7+24 s t^7-268 s^{10} y t^7-24 s^8 y t^7+3256 s^6 y t^7+1984 s^4 y t^7-140 s^2 y t^7-8 y t^7+54 s^{10} t^6-108 s^8 t^6-180 s^6 t^6-48 s^4 t^6-352 s^8 y^4 t^6-56 s^6 y^4 t^6-1456 s^4 y^4 t^6-1304 s^2 y^4 t^6-492 s^9 y^3 t^6+1344 s^7 y^3 t^6+232 s^5 y^3 t^6+544 s^3 y^3 t^6+1252 s y^3 t^6+414 s^2 t^6-188 s^{10} y^2 t^6+1298 s^8 y^2 t^6+2192 s^6 y^2 t^6-132 s^4 y^2 t^6+252 s^2 y^2 t^6-254 y^2 t^6-12 s^{11} y t^6+476 s^9 y t^6+392 s^7 y t^6-2856 s^5 y t^6-956 s^3 y t^6+12 s y t^6-4 t^6-36 s^9 t^5+40 s^7 t^5+64 s^5 t^5+312 s^7 y^4 t^5+888 s^5 y^4 t^5+744 s^3 y^4 t^5+40 s y^4 t^5+24 s^3 t^5+780 s^8 y^3 t^5-976 s^6 y^3 t^5-728 s^4 y^3 t^5-400 s^2 y^3 t^5-20 y^3 t^5+552 s^9 y^2 t^5-1760 s^7 y^2 t^5-1680 s^5 y^2 t^5-32 s^3 y^2 t^5+104 s y^2 t^5-92 s t^5+36 s^{10} y t^5-340 s^8 y t^5-696 s^6 y t^5+1368 s^4 y t^5+404 s^2 y t^5-4 y t^5+9 s^8 t^4-4 s^6 t^4-10 s^4 t^4-124 s^8 y^4 t^4+96 s^6 y^4 t^4-704 s^4 y^4 t^4-656 s^2 y^4 t^4-4 y^4 t^4-116 s^9 y^3 t^4-32 s^7 y^3 t^4-40 s^5 y^3 t^4+64 s^3 y^3 t^4+508 s y^3 t^4-4 s^2 t^4-2 s^{10} y^2 t^4-564 s^8 y^2 t^4+820 s^6 y^2 t^4+608 s^4 y^2 t^4+382 s^2 y^2 t^4-92 y^2 t^4-36 s^9 y t^4+64 s^7 y t^4+376 s^5 y t^4-288 s^3 y t^4-116 s y t^4+9 t^4+136 s^7 y^4 t^3+56 s^5 y^4 t^3+152 s^3 y^4 t^3+40 s y^4 t^3+260 s^8 y^3 t^3-336 s^6 y^3 t^3-8 s^4 y^3 t^3+112 s^2 y^3 t^3-28 y^3 t^3+4 s^9 y^2 t^3+224 s^7 y^2 t^3-184 s^5 y^2 t^3+64 s^3 y^2 t^3-108 s y^2 t^3+12 s^8 y t^3+16 s^6 y t^3-56 s^4 y t^3+16 s^2 y t^3+12 y t^3-16 s^8 y^4 t^2+24 s^6 y^4 t^2-128 s^4 y^4 t^2-136 s^2 y^4 t^2+4 s^9 y^3 t^2-160 s^7 y^3 t^2+104 s^5 y^3 t^2+52 s y^3 t^2-2 s^8 y^2 t^2-24 s^6 y^2 t^2+52 s^4 y^2 t^2-24 s^2 y^2 t^2-2 y^2 t^2+24 s^7 y^4 t-40 s^5 y^4 t+8 s^3 y^4 t+8 s y^4 t-4 s^8 y^3 t+16 s^6 y^3 t-24 s^4 y^3 t+16 s^2 y^3 t-4 y^3 t+s^8 y^4-4 s^6 y^4+6 s^4 y^4-4 s^2 y^4+y^4=0$$

这可用之前得到的复杂结果表示加以验证：
$$ \left\{\left\{\frac{(p+1)^2-p^2 u^2}{p u^2+p+1},\frac{2 p (p+1) u}{p u^2+p+1}\right\}\text{/.}\, \text{Solve}\left[p^2 q s t^2 u^2+p^2 q s t^2+p^2 q s u^2+p^2 q s+p^2 s t^2-2 p^2 s t u+p^2 s u^2+p q^2 s^2 t u^2+p q^2 s^2 t+p q^2 s t^2 u^2+p q^2 s t^2-p q^2 s u^2-p q^2 s-p q^2 t u^2-p q^2 t+p q s^2 t u^2+p q s^2 t+p q s t^2 u^2+3 p q s t^2-p q s u^2+p q s-p q t u^2-p q t+2 p s t^2-2 p s t u+q^2 s^2 t+q^2 s t^2-q^2 s-q^2 t+q s^2 t+2 q s t^2-q t+s t^2=0,u\right]\right\}\text{/.}\, \left\{p\to \text{Root}\left[\text{$\#$1}^4 \left(4 t^4+8 t^2+4\right)+\text{$\#$1}^3 \left(8 t^4+16 t^2+8\right)+\text{$\#$1}^2 \left(-4 s^2 t^4-4 s^2 t^2+4 s t^3+4 s t+4 t^4+8 t^2+4\right)+\text{$\#$1} \left(-4 s^2 t^4-4 s^2 t^2+4 s t^3+4 s t\right)-s^2 t^4+2 s t^3-t^2\&,4\right],q\to \text{Root}\left[\text{$\#$1}^4 \left(4 s^2+8 s t+4 t^2\right)+\text{$\#$1}^3 \left(8 s^2+16 s t+8 t^2\right)+\text{$\#$1}^2 \left(-4 s^2 t^2+4 s^2+12 s t+4 t^2\right)+\text{$\#$1} \left(4 s t-4 s^2 t^2\right)-s^2 t^2\&,4\right]\right\} $$

creasson

我们采用重心坐标方法，可以较简便地进行计算。先给出点$X$的求法:
令 $ X = \alpha A + \beta B + \gamma C $
$$ \alpha  + \beta  + \gamma  = 1 \space      .......    (1) $$
由椭圆性质首先有：
$$ AX + BX = AI + BI  \space      .......   (2) $$
$$ CX + AX = CI + AI    \space      .......   (3) $$
又由重心坐标的距离公式，有
$$ A{X^2} = \beta {c^2} + \gamma {b^2} - \alpha \beta {c^2} - \beta \gamma {a^2} - \gamma \alpha {b^2}     \space      .......    (4) $$
$$ B{X^2} = \gamma {a^2} + \alpha {c^2} - \alpha \beta {c^2} - \beta \gamma {a^2} - \gamma \alpha {b^2}   \space      .......   (5) $$
$$ C{X^2} = \alpha {b^2} + \beta {a^2} - \alpha \beta {c^2} - \beta \gamma {a^2} - \gamma \alpha {b^2}     \space      .......    (6) $$
然后我们设
$$ \mathop {BA}\limits^ \to   = \frac{{\left( {s + t} \right)\left( {1 - st} \right)}}{{s{{\left( {1 - it} \right)}^2}}}\mathop {BC}\limits^ \to $$
这样
$$ BC = a $$
$$ CA = b = \frac{{t\left( {1 + {s^2}} \right)}}{{s\left( {1 + {t^2}} \right)}}a $$
$$ AB = c = \frac{{\left( {s + t} \right)\left( {1 - st} \right)}}{{s\left( {1 + {t^2}} \right)}}a $$
$$ CA = b = \frac{{t\left( {1 + {s^2}} \right)}}{{s\left( {1 + {t^2}} \right)}}a $$
$$ AI = \frac{{t\left( {1 - st} \right)\sqrt {1 + {s^2}} }}{{s\left( {1 + {t^2}} \right)}}a $$
$$ BI = \frac{{1 - st}}{{\sqrt {1 + {t^2}} }}a $$
$$ CI = \frac{{t\sqrt {1 + {s^2}} }}{{\sqrt {1 + {t^2}} }}a $$
为了消去根式，我们再做代换
$$ s \to \frac{1}{2}\left( {\frac{1}{p} - p} \right),t \to \frac{1}{2}\left( {\frac{1}{q} - q} \right) $$
这样以上$(1)-(6)$式可以简化为有理式方程组，由此可以解出
$$ \alpha = -\frac{(p-1) (p+1) \left(q^2+1\right)^2 \left(p^2 q^2+p^2-4 p+q^2-4 q+1\right) \left(p^2 q^2+p^2+4 p+q^2+4 q+1\right)}{8 q (p+q) (p q-1) \left(p^4 q^4+10 p^4 q^2-7 p^4+8 p^3 q^3-24 p^3 q+2 p^2 q^4-4 p^2 q^2+10 p^2+8 p q^3+8 p q+q^4+2 q^2+1\right)} $$
$$ \beta = -\frac{\left(p^2+1\right)^2 (q-1) (q+1) \left(p^2 q^2-4 p^2 q+p^2-4 p q^2+q^2+1\right) \left(p^2 q^2+4 p^2 q+p^2+4 p q^2+q^2+1\right)}{8 p (p+q) (p q-1) \left(p^4 q^4+10 p^4 q^2-7 p^4+8 p^3 q^3-24 p^3 q+2 p^2 q^4-4 p^2 q^2+10 p^2+8 p q^3+8 p q+q^4+2 q^2+1\right)}$$
$$\gamma = \frac{(p q-p-q-1) (p q+p+q-1) \left(p^2 q^2-4 p^2 q+p^2+4 p+q^2+1\right) \left(p^2 q^2+4 p^2 q+p^2-4 p+q^2+1\right)}{8 p q \left(p^4 q^4+10 p^4 q^2-7 p^4+8 p^3 q^3-24 p^3 q+2 p^2 q^4-4 p^2 q^2+10 p^2+8 p q^3+8 p q+q^4+2 q^2+1\right)}$$
例如，三边为$a=3,b=4,c=5$的三角形$ABC$，可以给出
$$X=\frac{3 \left(85 \sqrt{2}+16 \sqrt{5}+271 \sqrt{10}+849\right) A-4 \left(-95 \sqrt{2}+292 \sqrt{5}+7 \sqrt{10}-639\right) B+5 \left(-127 \sqrt{2}+224 \sqrt{5}-157 \sqrt{10}+33\right) C}{5268}$$
替换 $ p\to q,q\to \frac{1-p q}{p+q} $ 可以给出点$ Y = \alpha _2 A + \beta _2 B + \gamma _2 C $
$$ \alpha_2 = -\frac{(p-1) (p+1) \left(q^2+1\right)^2 \left(p^2 q^2-4 p^2 q+p^2-4 p q^2+q^2+1\right) \left(p^2 q^2+4 p^2 q+p^2+4 p q^2+q^2+1\right)}{8 q (p+q) (p q-1) \left(p^4 q^4+2 p^4 q^2+p^4+8 p^3 q^3+8 p^3 q+10 p^2 q^4-4 p^2 q^2+2 p^2-24 p q^3+8 p q-7 q^4+10 q^2+1\right)} $$
$$ \beta_2 = -\frac{\left(p^2+1\right)^2 (q-1) (q+1) \left(p^2 q^2+p^2-4 p+q^2-4 q+1\right) \left(p^2 q^2+p^2+4 p+q^2+4 q+1\right)}{8 p (p+q) (p q-1) \left(p^4 q^4+2 p^4 q^2+p^4+8 p^3 q^3+8 p^3 q+10 p^2 q^4-4 p^2 q^2+2 p^2-24 p q^3+8 p q-7 q^4+10 q^2+1\right)}$$
$$\gamma_2 = \frac{(p q-p-q-1) (p q+p+q-1) \left(p^2 q^2+p^2-4 p q^2+q^2+4 q+1\right) \left(p^2 q^2+p^2+4 p q^2+q^2-4 q+1\right)}{8 p q \left(p^4 q^4+2 p^4 q^2+p^4+8 p^3 q^3+8 p^3 q+10 p^2 q^4-4 p^2 q^2+2 p^2-24 p q^3+8 p q-7 q^4+10 q^2+1\right)}$$
再替换 $ p\to q,q\to \frac{1-p q}{p+q} $ 可以给出点$ Z = \alpha _3 A + \beta _3 B + \gamma _3 C $
$$ \alpha_{3}= -\frac{(p-1) (p+1) \left(q^2+1\right)^2 \left(p^2 q^2-4 p^2 q+p^2+4 p+q^2+1\right) \left(p^2 q^2+4 p^2 q+p^2-4 p+q^2+1\right)}{8 q (p+q) (p q-1) \left(p^4 q^4+2 p^4 q^2+p^4-8 p^3 q^3-8 p^3 q+2 p^2 q^4-4 p^2 q^2+10 p^2-8 p q^3+24 p q+q^4+10 q^2-7\right)} $$
$$ \beta_{3} = -\frac{\left(p^2+1\right)^2 (q-1) (q+1) \left(p^2 q^2+p^2-4 p q^2+q^2+4 q+1\right) \left(p^2 q^2+p^2+4 p q^2+q^2-4 q+1\right)}{8 p (p+q) (p q-1) \left(p^4 q^4+2 p^4 q^2+p^4-8 p^3 q^3-8 p^3 q+2 p^2 q^4-4 p^2 q^2+10 p^2-8 p q^3+24 p q+q^4+10 q^2-7\right)} $$
$$ \gamma_{3} = \frac{(p q-p-q-1) (p q+p+q-1) \left(p^2 q^2+p^2-4 p+q^2-4 q+1\right) \left(p^2 q^2+p^2+4 p+q^2+4 q+1\right)}{8 p q \left(p^4 q^4+2 p^4 q^2+p^4-8 p^3 q^3-8 p^3 q+2 p^2 q^4-4 p^2 q^2+10 p^2-8 p q^3+24 p q+q^4+10 q^2-7\right)} $$

接下来我们再来求$AX,BY,CZ$的交点$T$。
一般情形，如果
$$ P_1 = {\alpha _1} Q_1 + {\beta _1} Q_2 + {\gamma _1} Q_3 $$
$$ P_2 = {\alpha _2} Q_1 + {\beta _2} Q_2 + {\gamma _2} Q_3 $$
$$ P_3 = {\alpha _3} Q_1 + {\beta _3} Q_2 + {\gamma _3} Q_3 $$
那么$P_1,P_2,P_3$三点共线的充要条件是
\[\det \left( {\begin{array}{*{20}{c}}
{{\alpha _1}}&{{\beta _1}}&{{\gamma _1}}\\
{{\alpha _2}}&{{\beta _2}}&{{\gamma _2}}\\
{{\alpha _3}}&{{\beta _3}}&{{\gamma _3}}
\end{array}} \right) = 0\]
我们令
$$ X = {\alpha _1}A + {\beta _1}B + {\gamma _1}C $$
$$ Y = {\alpha _2}A + {\beta _2}B + {\gamma _2}C $$
可知
\[T = \frac{{{\alpha _2}{\gamma _1}A + {\beta _1}{\gamma _2}B + {\gamma _1}{\gamma _2}C}}{{{\alpha _2}{\gamma _1} + {\beta _1}{\gamma _2} + {\gamma _1}{\gamma _2}}}\]
带入各式，可得$ T = \lambda A + \mu B + \nu C $
$$ \lambda = -\frac{(p-1) (p+1) \left(q^2+1\right)^2 \left(p^2 q^2-4 p^2 q+p^2+4 p+q^2+1\right) \left(p^2 q^2+4 p^2 q+p^2-4 p+q^2+1\right) \left(p^2 q^2-4 p^2 q+p^2-4 p q^2+q^2+1\right) \left(p^2 q^2+4 p^2 q+p^2+4 p q^2+q^2+1\right)}{8 q (p+q) (p q-1) \left(p^2 q^2+p^2-4 p q-3 q^2+1\right) \left(p^2 q^2-3 p^2-4 p q+q^2+1\right) \left(p^2 q^2+p^2+4 p q+q^2-3\right) \left(5 p^2 q^2+p^2-4 p q+q^2+1\right)} $$
$$ \mu = -\frac{\left(p^2+1\right)^2 (q-1) (q+1) \left(p^2 q^2+p^2-4 p q^2+q^2+4 q+1\right) \left(p^2 q^2-4 p^2 q+p^2-4 p q^2+q^2+1\right) \left(p^2 q^2+p^2+4 p q^2+q^2-4 q+1\right) \left(p^2 q^2+4 p^2 q+p^2+4 p q^2+q^2+1\right)}{8 p (p+q) (p q-1) \left(p^2 q^2+p^2-4 p q-3 q^2+1\right) \left(p^2 q^2-3 p^2-4 p q+q^2+1\right) \left(p^2 q^2+p^2+4 p q+q^2-3\right) \left(5 p^2 q^2+p^2-4 p q+q^2+1\right)} $$
$$ \nu = \frac{(p q-p-q-1) (p q+p+q-1) \left(p^2 q^2-4 p^2 q+p^2+4 p+q^2+1\right) \left(p^2 q^2+4 p^2 q+p^2-4 p+q^2+1\right) \left(p^2 q^2+p^2-4 p q^2+q^2+4 q+1\right) \left(p^2 q^2+p^2+4 p q^2+q^2-4 q+1\right)}{8 p q \left(p^2 q^2+p^2-4 p q-3 q^2+1\right) \left(p^2 q^2-3 p^2-4 p q+q^2+1\right) \left(p^2 q^2+p^2+4 p q+q^2-3\right) \left(5 p^2 q^2+p^2-4 p q+q^2+1\right)} $$
回代关系为
$$ p\to \sqrt{\frac{-4 \sqrt{a^2 b c+b^3 (-c)+2 b^2 c^2-b c^3}+a^2-b^2+6 b c-c^2}{-a^2+b^2+2 b c+c^2}} $$
$$ q\to \sqrt{\frac{-a^2-4 \sqrt{-a^3 c+2 a^2 c^2+a b^2 c-a c^3}+6 a c+b^2-c^2}{a^2+2 a c-b^2+c^2}} $$

数学星空

@creasson  
1. 向量BA与BC 的关系是怎么来的？？
2. s,t,p,q有几何意义吗？
3.最后一步回代到哪个关系式得到的p,q与a,b,c的关系？
3.除了内心I有此性质（AX,BY,CZ共点),是否还存在其它点也满足此性质？