共轭比概念证明一条与费马点有关的结论

dlsh

特殊三角形的费马点

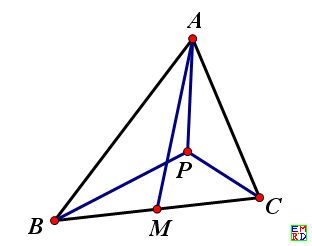角BAC=60度，∠APB=∠APC=∠BPC=120度，M是BC边中点，证明PA+PB+PC=2AM。
证明要点：假设P在原点，\(PA和PB长度等于r,r_{0},ω是单位根，c=1,所以a=r\omega,b=r_{0}\bar{\omega},由\angle BAC=\frac{\pi}{3}得\)
\(\frac{\frac{r \omega-1}{r \bar{\omega}-1}}{{\frac{r \omega-r_{0} \bar{\omega}}{r \bar{\omega}-r_{0}\omega}}}=\omega\)，解方程得\(r=\sqrt r_{0}\)，比较\(4AM^2与(1+r+r_{0})^2\)既可以证明。
   其实P是费马点，这里通过先构造费马点再找出A点，即使不知道也可以证明。也可以通过顶点直接构造费马点证明。
有关共轭比概念证明请参考签名中的链接，有学者认为用复斜率更合适。