- 注册时间
- 2018-12-8
- 最后登录
- 1970-1-1
- 威望
- 星
- 金币
- 枚
- 贡献
- 分
- 经验
- 点
- 鲜花
- 朵
- 魅力
- 点
- 上传
- 次
- 下载
- 次
- 积分
- 3549
- 在线时间
- 小时
|
马上注册,结交更多好友,享用更多功能,让你轻松玩转社区。
您需要 登录 才可以下载或查看,没有账号?欢迎注册
×
本帖最后由 dlpg070 于 2020-8-30 15:51 编辑
一个数值求解 2个函数2个自变量偏微分方程的例子
希望对倪鹏举的问题有启发
- Clear["Global`*"]
- Print["2个函数2个自变量 NDVolve求解的简单例子 "]
- s=NDSolve[{D[y1[x1,x2],x1]==D[y1[x1,x2],x2,x2],y1[0,x2]==0,y1[x1,0]==Sin[x1],y1[x1,5]==0,
- D[y2[x1,x2],x1]==D[y2[x1,x2],x2,x2],y2[0,x2]==0,y2[x1,0]==(Sin[x1])^2,y2[x1,5]==0},{y1,y2},(*{t,x}\[Element]\[CapitalOmega]*){x1,0,10},{x2,0,5},MaxStepSize->0.05]
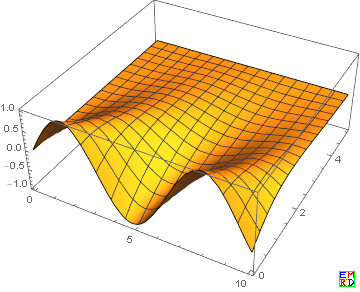
- Print["显示y1[x1,x2]:"]
- Plot3D[Evaluate[y1[x1,x2]/.s],{x1,0,10},{x2,0,5}, PlotRange->All]
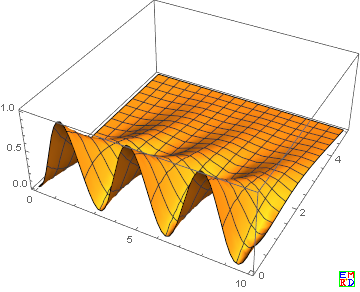
- Print["显示y2[x1,x2]:"]
- Plot3D[Evaluate[y2[x1,x2]/.s],{x1,0,10},{x2,0,5}, PlotRange->All]
|
-
ex1.png
-
ex2.png
|