过单位圆上一动点P的切线与另一个圆交于AB两点，求PA/PB的最大值

chyanog

已知点P为圆O: $x^2+y^2=1$上一个动点，O为坐标原点，过P点作圆O的切线与圆$(x-1)^2+(y-4)^2=6^2$交于A、B两点，则${PA}/{PB}$的最大值是多少？
有计算量比较小的方法吗？

wayne

$t=\frac{PA}{PB}  = - \frac{x_1-x_0}{x_2-x_0} $,对方程组$x \cos (\alpha )+y \sin (\alpha )=1,(x-1)^2+(y-4)^2=6^2$消元,得到$\frac{1}{2} (-16 \sin (\alpha )+19 \cos (2 \alpha )-17)+x^2+x (4 \sin (2 \alpha )-2 \cos (\alpha )+\cos (2 \alpha )-1)=0$
于是$t+\frac{1}{t}=-(\frac{x_1-x_0}{x_2-x_0} + \frac{x_2-x_0}{x_1-x_0}) =\frac{8 \sin (\alpha )-8 \sin (2 \alpha )+2 \cos (\alpha )+15 \cos (2 \alpha )+35}{4 \sin (\alpha )+\cos (\alpha )+9}$, 得到 $2<=t+\frac{1}{t}<=6$,所以$3-2 \sqrt{2}\leq t\leq 3+2 \sqrt{2$

chyanog

另一种方法，设$O_2$到AB的距离为$d$，$0<=d<=\sqrt{17}+1$,
$t={PA}/{PB}=\frac{AM+PM}{AM-PM}=\frac{\sqrt{36-d^2}+\sqrt{17-(d-1)^2}}{\sqrt{36-d^2}-\sqrt{17-(d-1)^2}}$,
$t+1/t=2 \left(d-10+\frac{64}{d-10}+19\right)$,
$2<=t+1/t<=6$,
$3-2 \sqrt{2}\leq t\leq 2 \sqrt{2}+3$

用合分比定理也可以
$\left(\frac{t-1}{t+1}\right)^2=\frac{17-(d-1)^2}{36-d^2}$,
$0\leq \left(\frac{t-1}{t+1}\right)^2\leq \frac{1}{2}$,
$3-2 \sqrt{2}\leq t\leq 2 \sqrt{2}+3$

数学星空

对于一般情形：

一个椭圆\(L_1: \frac{x^2}{a^2}+\frac{y^2}{b^2}=1\),位于椭圆\(L_2: \frac{(x-x_0)^2}{m^2}+\frac{(y-y_0)^2}{n^2}=1\)内，若直线外切于椭圆\(L_1\)于点\(P\)并交椭圆于\(L_2\)于\(A,B\)两点;

首先我们设\(A[x_1,y_1],B[x_2,y_2],P[x_3,y_3],x_3=\frac{a(1-t^2)}{1+t^2},y_3=\frac{2bt}{1+t^2}\)

则\(\frac{AP}{BP}=k\)满足方程：

2*a*b^2*m^2*n^2*t^8*x0 - 4*a*b^2*m^2*n^2*t^6*x0 - 16*a^2*b*m^2*n^2*t^5*y0 - 16*a^2*b*m^2*n^2*t^3*y0 + 4*a*b^2*m^2*n^2*t^2*x0 - b^2*m^4*n^2*t^8 + b^2*m^4*t^8*y0^2 - 4*b^3*m^4*t^7*y0 + 8*a^3*n^4*t^6*x0 - 4*a^2*m^2*n^4*t^6 + 4*a^2*n^4*t^6*x0^2 + 4*b^3*m^4*t^5*y0 - 8*a^2*m^2*n^4*t^4 + 8*a^2*n^4*t^4*x0^2 + 2*b^2*m^4*n^2*t^4 - 2*b^2*m^4*t^4*y0^2 + 4*b^3*m^4*t^3*y0 - 8*a^3*n^4*t^2*x0 - 4*a^2*m^2*n^4*t^2 + 4*a^2*n^4*t^2*x0^2 - 4*b^3*m^4*t*y0 + a^2*b^2*m^2*n^2 + b^2*m^2*n^2*x0^2 + a^2*b^2*m^2*n^2*t^8 + b^2*m^2*n^2*t^8*x0^2 - 4*a^2*b^2*m^2*n^2*t^6 + 4*a^2*m^2*n^2*t^6*y0^2 + 22*a^2*b^2*m^2*n^2*t^4 + 8*a^2*m^2*n^2*t^4*y0^2 - 2*b^2*m^2*n^2*t^4*x0^2 - 4*a^2*b^2*m^2*n^2*t^2 + 4*a^2*m^2*n^2*t^2*y0^2 - 2*a*b^2*m^2*n^2*x0 + b^2*m^4*y0^2 + 4*b^4*m^4*t^6 + 4*b^4*m^4*t^2 - b^2*m^4*n^2 + 4*a^4*n^4*t^2 - 8*b^4*m^4*t^4 - 8*a^4*n^4*t^4 + 4*a^4*n^4*t^6 + (a^2*b^2*m^2*n^2*t^8 + 2*a*b^2*m^2*n^2*t^8*x0 - b^2*m^4*n^2*t^8 + b^2*m^4*t^8*y0^2 + b^2*m^2*n^2*t^8*x0^2 - 4*b^3*m^4*t^7*y0 + 4*a^4*n^4*t^6 + 8*a^3*n^4*t^6*x0 - 4*a^2*b^2*m^2*n^2*t^6 - 4*a^2*m^2*n^4*t^6 + 4*a^2*m^2*n^2*t^6*y0^2 + 4*a^2*n^4*t^6*x0^2 - 4*a*b^2*m^2*n^2*t^6*x0 + 4*b^4*m^4*t^6 - 16*a^2*b*m^2*n^2*t^5*y0 + 4*b^3*m^4*t^5*y0 - 8*a^4*n^4*t^4 + 22*a^2*b^2*m^2*n^2*t^4 - 8*a^2*m^2*n^4*t^4 + 8*a^2*m^2*n^2*t^4*y0^2 + 8*a^2*n^4*t^4*x0^2 - 8*b^4*m^4*t^4 + 2*b^2*m^4*n^2*t^4 - 2*b^2*m^4*t^4*y0^2 - 2*b^2*m^2*n^2*t^4*x0^2 - 16*a^2*b*m^2*n^2*t^3*y0 + 4*b^3*m^4*t^3*y0 + 4*a^4*n^4*t^2 - 8*a^3*n^4*t^2*x0 - 4*a^2*b^2*m^2*n^2*t^2 - 4*a^2*m^2*n^4*t^2 + 4*a^2*m^2*n^2*t^2*y0^2 + 4*a^2*n^4*t^2*x0^2 + 4*a*b^2*m^2*n^2*t^2*x0 + 4*b^4*m^4*t^2 - 4*b^3*m^4*t*y0 + a^2*b^2*m^2*n^2 - 2*a*b^2*m^2*n^2*x0 - b^2*m^4*n^2 + b^2*m^4*y0^2 + b^2*m^2*n^2*x0^2)*k^2 + (-2*a^2*b^2*m^2*n^2*t^8 - 4*a*b^2*m^2*n^2*t^8*x0 + 2*b^2*m^4*n^2*t^8 + 2*b^2*m^4*t^8*y0^2 - 2*b^2*m^2*n^2*t^8*x0^2 + 16*a^2*b*m^2*n^2*t^7*y0 + 16*a*b*m^2*n^2*t^7*x0*y0 - 8*b^3*m^4*t^7*y0 + 8*a^4*n^4*t^6 + 16*a^3*n^4*t^6*x0 - 24*a^2*b^2*m^2*n^2*t^6 + 8*a^2*m^2*n^4*t^6 - 8*a^2*m^2*n^2*t^6*y0^2 + 8*a^2*n^4*t^6*x0^2 - 24*a*b^2*m^2*n^2*t^6*x0 + 8*b^4*m^4*t^6 + 16*a^2*b*m^2*n^2*t^5*y0 + 16*a*b*m^2*n^2*t^5*x0*y0 + 8*b^3*m^4*t^5*y0 - 16*a^4*n^4*t^4 + 20*a^2*b^2*m^2*n^2*t^4 + 16*a^2*m^2*n^4*t^4 - 16*a^2*m^2*n^2*t^4*y0^2 + 16*a^2*n^4*t^4*x0^2 - 16*b^4*m^4*t^4 - 4*b^2*m^4*n^2*t^4 - 4*b^2*m^4*t^4*y0^2 + 4*b^2*m^2*n^2*t^4*x0^2 + 16*a^2*b*m^2*n^2*t^3*y0 - 16*a*b*m^2*n^2*t^3*x0*y0 + 8*b^3*m^4*t^3*y0 + 8*a^4*n^4*t^2 - 16*a^3*n^4*t^2*x0 - 24*a^2*b^2*m^2*n^2*t^2 + 8*a^2*m^2*n^4*t^2 - 8*a^2*m^2*n^2*t^2*y0^2 + 8*a^2*n^4*t^2*x0^2 + 24*a*b^2*m^2*n^2*t^2*x0 + 8*b^4*m^4*t^2 + 16*a^2*b*m^2*n^2*t*y0 - 16*a*b*m^2*n^2*t*x0*y0 - 8*b^3*m^4*t*y0 - 2*a^2*b^2*m^2*n^2 + 4*a*b^2*m^2*n^2*x0 + 2*b^2*m^4*n^2 + 2*b^2*m^4*y0^2 - 2*b^2*m^2*n^2*x0^2)*k=0

上式关于\(t\)求导并联立上式消元可以得到k取极值时的方程（表达式太长，略去）

例如：

对于\(a = 2, b = 1, m = 10, n = 6, x_0 = 2, y_0 = 2\)

代入得到：

-262400*k^2*t^8 - 80000*k^2*t^7 + 684800*k*t^8 - 1586624*k^2*t^6 + 761600*k*t^7 - 262400*t^8 - 380800*k^2*t^5 + 3738752*k*t^6 - 80000*t^7 - 2838400*k^2*t^4 + 1081600*k*t^5 - 1586624*t^6 - 380800*k^2*t^3 + 5958400*k*t^4 - 380800*t^5 - 1803200*k^2*t^2 + 160000*k*t^3 - 2838400*t^4 - 80000*k^2*t + 3766400*k*t^2 - 380800*t^3 - 320000*k^2 - 160000*k*t - 1803200*t^2 + 800000*k - 80000*t - 320000=0

对上式关于\(t\)求导并联立上式消元\(t\)得到：

30082656341703358469277587865600000000*k^16 - 300953784148725256036394257612800000000*k^15 + 2934162696746981709158211492249600000000*k^14 - 21079060077706214283946456252416000000000*k^13 + 90809841658981202084239235245670400000000*k^12 - 249397191252899066597233587860275200000000*k^11 + 479934478610046242187927515194982400000000*k^10 - 698229412196511735232110375469056000000000*k^9 + 791873567235670357454077893279744000000000*k^8 - 698229412196511735232110375469056000000000*k^7 + 479934478610046242187927515194982400000000*k^6 - 249397191252899066597233587860275200000000*k^5 + 90809841658981202084239235245670400000000*k^4 - 21079060077706214283946456252416000000000*k^3 + 2934162696746981709158211492249600000000*k^2 - 300953784148725256036394257612800000000*k + 30082656341703358469277587865600000000=0

解得\(k={0.4037716479, 0.4624518570, 2.162387251, 2.476647395}\)

则可以得到：\(k=2.476647395,t=4.245867034\),进一步得到\(x_1 = 5.390040146, x_2 = -4.688785674, y_1 = 7.644709558, y_2 = -2.460230110, x_3 = -1.789776703, y_3 = 0.4462900832\)

画图得到：



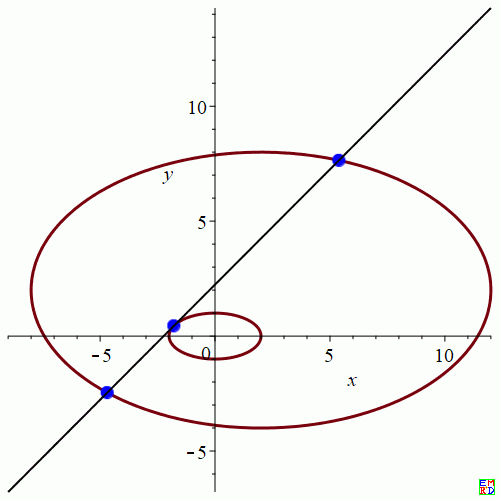
若\(a = r, b = r, m = R, n = R\)则化为两个圆的情形：

一般点的\(k\)满足方程：

\(R^2k^2t^4 - k^2r^2t^4 - 2k^2rt^4x_0 - k^2t^4x_0^2 - k^2t^4y_0^2 - 2R^2kt^4 + 4k^2rt^3y_0 + 2kr^2t^4 + 4krt^4x_0 + 2kt^4x_0^2 - 2kt^4y_0^2 + 2R^2k^2t^2 + R^2t^4 - 2k^2r^2t^2 - 2k^2t^2x_0^2 - 2k^2t^2y_0^2 - 8krt^3y_0 - 16kt^3x_0y_0 - r^2t^4 - 2rt^4x_0 - t^4x_0^2 - t^4y_0^2 - 4R^2kt^2 + 4k^2rty_0 + 4kr^2t^2 - 12kt^2x_0^2 + 12kt^2y_0^2 + 4rt^3y_0 + R^2k^2 + 2R^2t^2 - k^2r^2 + 2k^2rx_0 - k^2x_0^2 - k^2y_0^2 - 8krty_0 + 16ktx_0y_0 - 2r^2t^2 - 2t^2x_0^2 - 2t^2y_0^2 - 2R^2k + 2kr^2 - 4krx_0 + 2kx_0^2 - 2ky_0^2 + 4rty_0 + R^2 - r^2 + 2rx_0 - x_0^2 - y_0^2=0\)

\(k\)取极值时满足方程：
\(-k^4r^2 + 4R^2k^3 - 4k^3x_0^2 - 4k^3y_0^2 - 8R^2k^2 + 2k^2r^2 - 8k^2x_0^2 - 8k^2y_0^2 + 4R^2k - 4kx_0^2 - 4ky_0^2 - r^2=0\)

例本贴取\(r=1,R=6,x_0=1,y_0=4\)代入上式得到：\((k^2 - 6k + 1)(k^2 - 70k + 1)=0\)

hujunhua

可将大圆的圆心放在 y 轴上以正其形， 方程变为   `x^2+(y-\sqrt{17})^2=6^2`
在弦AB所在直线上找到 P 的以 A, B 为基点的调和共轭点C，于是
求PA/PB的最大值，即转化为求CA/CB 的最大值。
C的轨迹为下图中的红色剪刀形曲线，有一自交点在 y 轴上。
目测 驻点即为这个自交点。这时CA为剪刀形轨迹曲线一支的法线。

hujunhua

在原图上找驻点 P 有两个位置，其中一个位置在 x 轴上。
这验证了上图的目测是正确的。显然，`C = -O_2`.
评曰：`P_1`在 x 轴上看似很特别，其实不过是数据精巧，不具代数性。`C=-O_2`可能才具有代数不变性。

hujunhua

构图由大圆半径R，小圆半径 r (不妨固定为1）和圆心距 d 决定。
试了一下，`OC(R, r, d)=-d`并不恒成立，也就是说， `C=-O_2`也不是代数不变的。
只有驻点 C 位于连心线上是不变的。C点的计算方法如下：
两圆都写成二次型形式，圆`O`和圆`O_2`对应的对称矩阵分别为\[M=\pmatrix{1&0&0\\0&1&0\\0&0&-1}，M_2=\pmatrix{1&0&-1\\0&1&-4\\-1&-4&-19}\]C点关于两圆的极线是相同的，把C的坐标写成`x=(x_1,x_2,1)`的形式, 便有`M_2x=\lambda Mx `, 即`(M_2-\lambda M)x=0`,
对应的特征方程 `|M_2-\lambda M|=0`的有3个根1, 2, 18, 其中1对应于极配“无穷远点-连心线”，是恒有的1个根，舍去。
剩余两根2, 18正好对应两个关联极配（两个极配的极点刚好在对方的极线上）。
`(M_2-2M)x=\pmatrix{-1&0&-1\\0&-1&-4\\-1&-4&-17}x=0`对应的解为`x=(-1,-4,1)`即为所求的C点。
`(M_2-18M)x=0`对应的解为`x=(-1,-4,17)`即 $(-1/17,-4/17,1)$, 为C点的极线与连心线的交点。 它在圆内，舍弃。

hujunhua

从圆反演的观点看，C关于两圆的反演像是相同的（图中的D），因此设OC=h, 则有\[\frac{R^2}{h+d}=\frac{r^2}h+d\]将h=d代入可得  `R^2=2(d^2+r^2)`, 这是`C=-O_2`的条件。本题正好符合这个条件。

数学星空

根据楼上老胡的求解方案，将计算结果汇集如下：

对于小圆\(O_1 : x^2+y^2=r^2\) 内含于大圆\(O_2: (x-x_0)^2+(y-y_0)^2=R^2\)

的驻点\(C[x_1,y_1]\)且

\(x_1=-\frac{x_0}{m-1},y_1=-\frac{y_0}{m-1}\)

通过驻点C的直线切小圆\(O_1\)于点\(P[x_2,y_2]\),并交大圆于\(A[x_4,y_4],B[x_3,y_3]\)两点

设\(x_2=\frac{r(1-t^2)}{1+t^2},y_2=\frac{2tr}{1+t^2}\)

\(m\)与\(t\)满足下列方程：

-m^2*r^2 + R^2*m + m*r^2 - m*x0^2 - m*y0^2 - R^2=0

(R^2*x0 - r^2*x0 - 2*r*x0^2 - r*y0^2 - x0^3 - x0*y0^2)*t^4 + (-2*R^2*y0 + 2*r^2*y0 + 4*r*x0*y0 + 2*x0^2*y0 + 2*y0^3)*t^3 - 6*r*t^2*y0^2 + (-2*R^2*y0 + 2*r^2*y0 - 4*r*x0*y0 + 2*x0^2*y0 + 2*y0^3)*t - R^2*x0 + r^2*x0 - 2*r*x0^2 - r*y0^2 + x0^3 + x0*y0^2=0

\([x_3,y_3],[x_4,y_4]\)满足下列关于\([x,y]\)的方程

(t^4 + 2*t^2 + 1)*x^2 + (2*r*t^4 - 4*t^3*y0 - 8*t^2*x0 + 4*t*y0 - 2*r)*x + r^2*t^4 - 4*r*t^3*y0 - 4*R^2*t^2 + 2*r^2*t^2 + 4*x0^2*t^2 + 4*t^2*y0^2 - 4*r*t*y0 + r^2=0

(t^4 + 2*t^2 + 1)*y^2 + (-2*t^4*y0 - 4*r*t^3 - 4*t^3*x0 + 4*t^2*y0 - 4*r*t + 4*t*x0 - 2*y0)*y - R^2*t^4 + r^2*t^4 + 2*r*t^4*x0 + t^4*x0^2 + t^4*y0^2 + 2*R^2*t^2 + 2*r^2*t^2 - 2*x0^2*t^2 - 2*t^2*y0^2 - R^2 + r^2 - 2*r*x0 + x0^2 + y0^2=0

则\(k=\frac{PA}{PB}=\sqrt{\frac{(x_4-x_2)^2+(y_4-y_2)^2}{(x_4-x_2)^2+(y_4-y_2)^2}}\)

对于本例：\(r=1,R=6,x_0=1,y_0=4\)代入上面方程解之

\({x_1=-1, x_2 = \frac{15}{17}, x_3 = \frac{47-32\sqrt{2}}{17}, x_4 = \frac{47+32\sqrt{2}}{17}, y_1 = -4, y_2 =-\frac{8}{17}, y_3 =\frac{52-60\sqrt{2}}{17}, y_4 =\frac{52+60\sqrt{2}}{17},k=3+2\sqrt{2}}\)

mathematica

1. Clear["Global`*"];
   
2. {xp,yp}={Cos[t],Sin[t]};
   
3. (*利用垂直与点在圆上求解出另外两个点*)
   
4. ans=Solve[{(x-xp)*xp+(y-yp)*yp==0,(x-1)^2+(y-4)^2==6^2},{x,y}]//FullSimplify;
   
5. aaa={x,y}/.ans
   
6. xa=aaa[[1,1]];
   
7. xb=aaa[[2,1]];
   
8. (*目标函数*)
   
9. tt=(xa-xp)/(xp-xb);
   
10. (*简化目标函数*)
    
11. tt2=FullSimplify[tt+1/tt]
    
12. (*目标函数绘图*)
    
13. Plot[tt2,{t,0,2*Pi},AxesOrigin->{0,0}]
    
14. Maximize[{tt2,0<=t<=2*Pi},t]
    

复制代码