有线性阻力的抛射体运动方程当中为什么包含自然常数e？

wufaxian

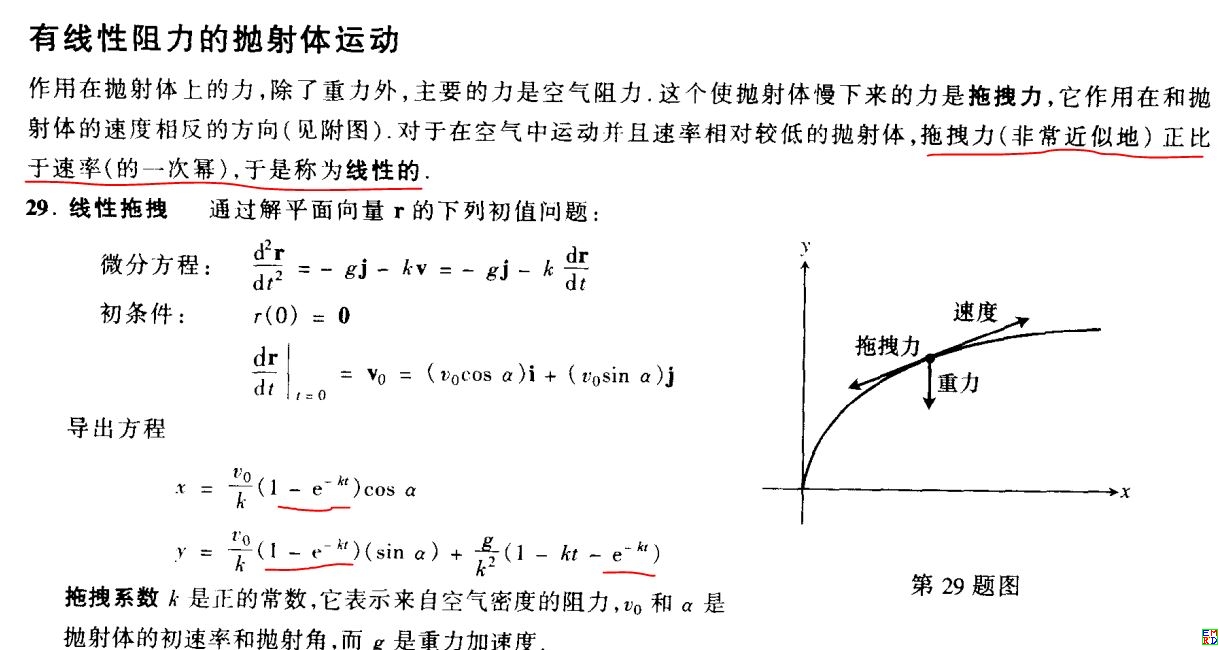
请看上图 r''=gj-kv
一次积分以后 r'=v=g*t*j-k*r*t+c   (c是不定积分待确定的未知常数)

考虑到初值 ：V0=V0*cos(a)*i+V0*sin(a)*j
                        t=0
带入一次积分后的结果：v=0+0+c=V0*cos(a)*i+V0*sin(a)*j  因此可知c=V0*cos(a)*i+V0*sin(a)*j

于是有r'=v=g*t*j-krt+V0*cos(a)*i+V0*sin(a)*j =-krt+V0*cos(a)*i+（V0*sin(a)-g*t)*j

在进行第二次积分：
为什么i 和j 的系数就会变为图中红线部分的x 和y的表达式呢？其中为什么会出现自然常数e呢？


利用sage对最后一步进行积分。代码如下：
x, y, g,k,t,j,i,v,r,a = var('x,y,g,k,t,j,i,v,r,a')
latex(integral(-(g*t*j)-(k*r)+v*cos(a)*i+v*sin(a)*j, t))

结果如下：
-\frac{1}{2} \, g j t^{2} + i t v \cos\left(a\right) + j t v \sin\left(a\right) - k r t