今年全国高中联赛题新结论

dlsh

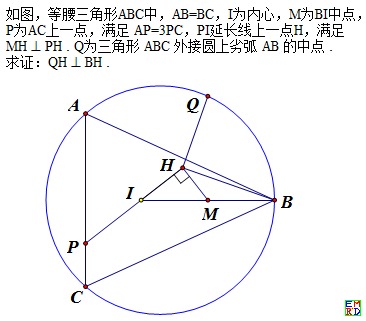
证明：假设A、B是两点，P是直线外一点，P在AB直线的垂足H可以表示为：
\(h=\frac{1}{2}\left[h+\frac{p(a-b)}{\bar {a}-\bar{b}}+\frac{\bar {a}b-a\bar {b}}{\bar {a}-\bar{b}}\right]\),具体推导参考链接中的国际学术会议论文。
把△ABC的外接圆看作单位圆，且B在实轴上，易得：
\(b=1,a=\bar{c}=q^2，c=\bar{a}=\frac{1}{q^2}\)，\(f=\frac{1}{4}(q^2+\frac{3}{q^2}),\bar{f}=\frac{1}{4}(3q^2+\frac{1}{q^2}),i=\bar{i}=q+\frac{1}{q}-1,m=\bar{m}=\frac{1}{2}(q+\frac{1}{q})\)
Mathematica计算得：
\(h=\frac{2q^2-q+1}{3q-1}\)
所以：\(h-q=\frac{1-q^2}{3q-1}，h-b=\frac{2(q-1)^2}{3q-1}\),\(\frac{h-q}{h-b}=\frac{1+q}{2(1-q)}\)
结论是显然的，以上系列表达式简单变形后可以得到对应的结论 ，图中用红色标记。

chyanog

mathematica

我记得好像有机械证明，好像是中科院的，对付这些平面几何应该问题不大