求证四面体的一个几何不等式

lihpb01

R为四面体ABCD的外接球半径
S_i为四面体ABCD的各侧面的面积，1≤i≤4。
求证

lihpb01

等号当且仅当该四面体为正四面体时成立

zeroieme

纲量不一致

mathe

应该是问题，球的内接四面体中表面积最大是否是正四面体。

lihpb01

一楼写错，半径是平方项

mathe

对于单位球上四面体ABCD,外心O。我们先查看固定B,C,D三个点，A可以在球面自由移动时，A所在位置需要满足什么条件才使得四面体表面积最大。
为此，我们记b=CD,c=DB,d=BC. 而A向CD,DB,BC做高对应的向量分别为\(\vec{h}_b(A),\vec{h}_c(A),\vec{h}_d(A)\).
我们要计算$b|\vec{h}_b(A)|+c|\vec{h}_c(A)|+d|\vec{h}_d(A)|$在约束条件$|\vec{A}|^2=1$的最大值。
使用拉格朗日乘数法,得到\(b\nabla|\vec{h}_b(A)|+c\nabla|\vec{h}_c(A)|+d|\vec{h}_d(A)|-2\lambda \vec{A}=0\)
为了能够更容易的计算\(\nabla|\vec{h}_b(A)|\),我们可以重建坐标，选择CD为x轴方向，$\vec{h}_b(A)$为y轴方向，于是这时\(|\vec{h}_b(A)|=\sqrt{y^2+z^2}\)
计算可以得出\(\nabla|\vec{h}_b(A)| = -\frac{\vec{h}_b(A)}{|\vec{h}_b(A)|}\)，这个表达形式和坐标的选择没有关系。
由此得出四面体表面积取极值时，要求
\(\frac{b\vec{h}_b(A)}{|\vec{h}_b(A)|}+\frac{c\vec{h}_c(A)}{|\vec{h}_c(A)|}+\frac{d\vec{h}_d(A)}{|\vec{h}_d(A)|}+2\lambda \vec{A}=0\).

现在现在任意选择一个和\(\vec{A}\)垂直的平面，并且三角形BCD在其上投影为B'C'D',而且b'=C'D',c'=D'B',d'=B'C'.
假设A在B'C'D'平面投影为$A_0$, 设单位向量\(\frac{\vec{h}_b(A)}{|\vec{h}_b(A)|},\frac{\vec{h}_b(A)}{|\vec{h}_b(A)|},\frac{\vec{h}_b(A)}{|\vec{h}_b(A)|}\)等在平面B'C'D'的投影分别为向量\(\vec{e},\vec{f},\vec{g}\),于是要求\(b\vec{e}+c\vec{f}+d\vec{g}=\vec{0}\)

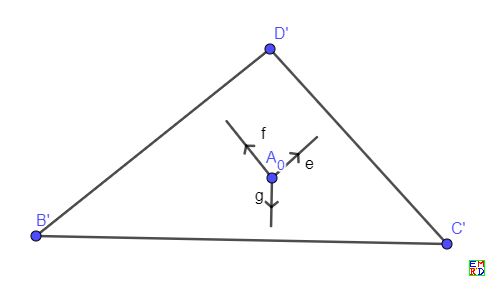
可以看出如果分别将\(\vec{e},\vec{f},\vec{g}\)同时顺时针旋转90°，旋转后方向分别同\(\vec{C'D'},\vec{D'B'},\vec{B'C'}\)相同。由于\(\vec{C'D'}+\vec{D'B'}+\vec{B'C'}=\vec{0}\)，
可以从几何意义看出\(\alpha \vec{C'D'}+\beta \vec{D'B'}\)当且仅当\(\alpha=\beta\)时才平行\(\vec{D'B'}\),所以我们得出只能\(|b\vec{e}|:|c\vec{f}|:|d\vec{g}|=b':c':d'\)时极值条件才能取到, 也就是\(|\vec{e}|:|\vec{f}|:|\vec{g}|=\frac{b'}{b}:\frac{c'}{c}:\frac{d'}{d}\)的时候四面体表面积才取到极值, 而这个条件等价于
$\vec{h}_d(A)$和OA的夹角的正弦值与BC和OA夹角的正弦值的比值 = $\vec{h}_b(A)$和OA夹角的正弦与CD和OA夹角的正弦值 = $\vec{h}_c(A)$和OA夹角的正弦与DB和OA夹角的正弦值

mathe

搜索了一篇文章不错:http://gtsintsifas.com/wp-conten ... 04/Cminmaxtetra.pdf
定理一：体积相同的四面体中，正四面体表面积最小。
定理二：表面积相同的四面体中，正四面体体积最大。
定理三：外切于给定球的四面体中，正四面体体积最小。
定理四：外切于给定球的四面体中，正四面体表面积最小。
定理五：内接于给定球的四面体中，正四面体体积最大。
定理六：内接于给定球的四面体中，正四面体表面积最大。
定理七：内接于给定球的四面体中，正四面体棱长之和最大。

creasson

四面体外心$O$与重心$G$的距离平方为：
$OG^2 = R^2 - \frac{1}{16}\left( AB^2 + AC^2 + AD^2 + BC^2 + BD^2 + CD^2 \right) \ge 0 $
再由三角形的不等式：
$ a^2 + b^2 + c^2 \ge ab + bc + ca \ge 4\sqrt 3 S $
联合即得。