- 注册时间
- 2008-11-26
- 最后登录
- 1970-1-1
- 威望
- 星
- 金币
- 枚
- 贡献
- 分
- 经验
- 点
- 鲜花
- 朵
- 魅力
- 点
- 上传
- 次
- 下载
- 次
- 积分
- 149506
- 在线时间
- 小时
|
楼主 |
发表于 2021-5-30 12:22:42
|
显示全部楼层
本帖最后由 mathematica 于 2021-5-30 12:23 编辑
- Clear["Global`*"];(*mathematica11.2,win7(64bit)Clear all variables*)
- (*计算余弦值子函数,利用三边计算余弦值*)
- cs[a_,b_,c_]:=(a^2+b^2-c^2)/(2*a*b)
- (*假设CB=CA=x,BO=y,计算∠BCO的余弦值,计算∠ACO的余弦值*)
- (*利用余弦定理计算两个角的余弦值,互余角的余弦值的平方和等于1*)
- aaa=cs[x,2,y]^2+cs[2,x,2]^2-1
- bbb=Numerator@Together[aaa](*只取分子,得到约数条件*)
- f=y+t*bbb(*建立目标函数,求y的最大值*)
- ans=Solve[D[f,{{x,y,t}}]==0,{x,y,t},Reals]//FullSimplify(*拉格朗日乘子法,求偏导数,解方程组*)
- Grid[ans,Alignment->Left]
- g=x+t*bbb(*建立目标函数,求x的最大值*)
- out=Solve[D[g,{{x,y,t}}]==0,{x,y,t},Reals]//FullSimplify(*拉格朗日乘子法,求偏导数,解方程组*)
- Grid[out,Alignment->Left]
- fi=ContourPlot[bbb==0,{x,-6,6},{y,-6,6}](*隐函数绘图,看看约数条件的图像是什么样*)
一切思路写在代码注释里面!
约束条件是
\[2 x^4-2 x^2 y^2-8 x^2+y^4-8 y^2+16=0\]
求y极值的方程组的解是(只有实数解)
\[\begin{array}{lll}
x\to -2 \sqrt{2-\sqrt{2}} & y\to 2-2 \sqrt{2} & t\to \frac{1}{64} \left(-\sqrt{2}-2\right) \\
x\to -2 \sqrt{2-\sqrt{2}} & y\to 2 \left(\sqrt{2}-1\right) & t\to \frac{1}{64} \left(\sqrt{2}+2\right) \\
x\to 2 \sqrt{2-\sqrt{2}} & y\to 2-2 \sqrt{2} & t\to \frac{1}{64} \left(-\sqrt{2}-2\right) \\
x\to 2 \sqrt{2-\sqrt{2}} & y\to 2 \left(\sqrt{2}-1\right) & t\to \frac{1}{64} \left(\sqrt{2}+2\right) \\
x\to -2 \sqrt{\sqrt{2}+2} & y\to -2 \left(\sqrt{2}+1\right) & t\to \frac{1}{64} \left(2-\sqrt{2}\right) \\
x\to -2 \sqrt{\sqrt{2}+2} & y\to 2 \left(\sqrt{2}+1\right) & t\to \frac{1}{64} \left(\sqrt{2}-2\right) \\
x\to 2 \sqrt{\sqrt{2}+2} & y\to -2 \left(\sqrt{2}+1\right) & t\to \frac{1}{64} \left(2-\sqrt{2}\right) \\
x\to 2 \sqrt{\sqrt{2}+2} & y\to 2 \left(\sqrt{2}+1\right) & t\to \frac{1}{64} \left(\sqrt{2}-2\right) \\
\end{array}\]
求x极值的方程组的解是(只有实数解)
\[\begin{array}{lll}
x\to -4 & y\to -2 \sqrt{5} & t\to \frac{1}{128} \\
x\to -4 & y\to 2 \sqrt{5} & t\to \frac{1}{128} \\
x\to 4 & y\to -2 \sqrt{5} & t\to -\frac{1}{128} \\
x\to 4 & y\to 2 \sqrt{5} & t\to -\frac{1}{128} \\
\end{array}\]
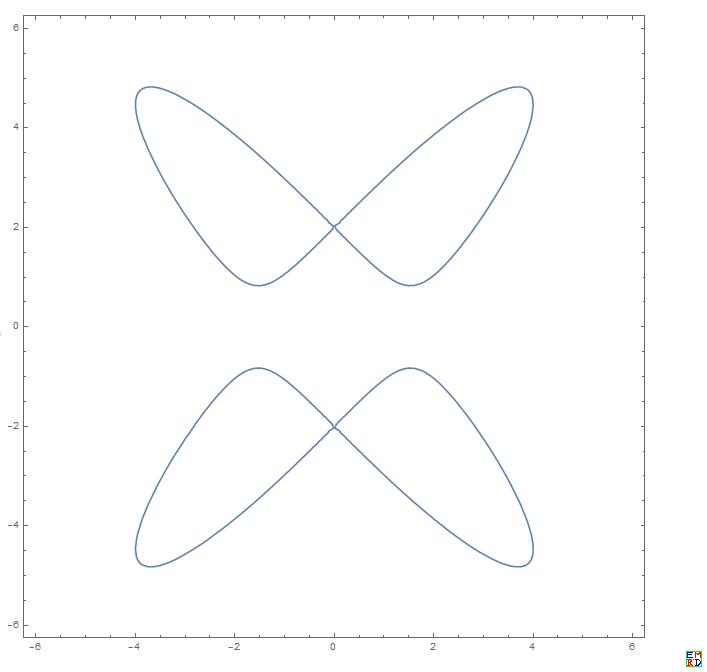
约束条件的图像是
补充内容 (2021-6-1 13:39):
看起来像蝴蝶的翅膀 |
-
|