数学研发网设为首页收藏本站
切换到窄版

 找回密码
 欢迎注册
数学研发论坛»论坛 › 【数学研究】 › 刨根究底 › 有黄绿红三种颜色的珠子各 4、4、1个。用它们穿成 9 颗 ...
12下一页
返回列表 发新帖
查看: 28276|回复: 18

[讨论] 有黄绿红三种颜色的珠子各 4、4、1个。用它们穿成 9 颗珠子的手串，有多少种组合？

[复制链接]
TSC999
发表于 2021-7-4 23:19:56 | 显示全部楼层 |阅读模式

马上注册，结交更多好友，享用更多功能，让你轻松玩转社区。

您需要 登录 才可以下载或查看，没有账号？欢迎注册

×
有大小相同的珠子共 9 个，其中黄色的 4 颗，绿色的 4 颗，红色的 1 颗。用它们穿成 9 颗珠子的手串，有多少种不同的花色组合？

可以参考常新德（河南永城职业学院老师）写的论文。网址：https://max.book118.com/html/2017/0729/125132578.shtm

本帖的目的，就是探讨一下上面这篇论文中的公式是否全都正确。


补充内容 (2021-7-9 08:47):
5 天后编写了计算程序（见后面）。用程序计算 3 种颜色（1 红、4 黄、4 绿）的花色组合数为 38 种。用常新德公式计算也是 38 种。即在 m=3，n1=1，n2=4，n3=4 时程序与公式计算结果相同。但其它情况下有不一致的。
毋因群疑而阻独见　　毋任己意而废人言
毋私小惠而伤大体　　毋借公论以快私情
回复

使用道具 举报

TSC999
 楼主| 发表于 2021-7-7 21:58:57 | 显示全部楼层
本帖最后由 TSC999 于 2021-7-8 06:06 编辑

本帖目的在主帖中说了，是为了改进常新德老师（河南永城职业学院）大约在 2008 年写的论文《有重复元素的圆排列和环排列的计数问题》。见网址：https://max.book118.com/html/2017/0729/125132578.shtm
对于有 m 种颜色，每种颜色的珠子分别有 n(1)、n(2)、......、n(m) 颗，能穿成多少种花色的手串问题（手串共有 n(1)+n(2)+......+n(m) 颗珠子），论文给出的计算公式中，要求各种颜色的珠子数目，至多只能有两个是奇数。
这就限制了应用范围。比如现在有 3 种颜色红、绿、黄，其中红珠 3 颗，绿珠 1 颗， 黄珠 1 颗，由于每种颜色的珠子数目都是奇数，不符合公式约定的 “珠子数目至多只能有两个是奇数” 这一要求， 所以计算结果是一个分数。
如果把分数结果取整，舍掉小数部分，好像能得到正确结果。为了验证这个想法是否正确，我们必须事先写一个计算程序作为裁判，以便由程序给出一个可信赖的结果。

我用 mathematica 初步写了一个程序，似能正确运行，但是尚缺最后一步即如何加上一个循环语句。
在程序中设定共有红、绿、黄 3 种颜色即 m=3。其中红珠 3 颗，绿珠 1 颗，黄珠 1 颗。对于这种非常简单的情况，只有 2 种可能的花色，见下图。

2 种花色.png

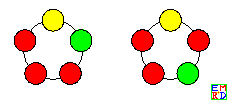
程序调试成功后，可将颜色数目和各色珠子数量随意修改。目前程序尚未最终完成，但程序能给出正确的计算结果。程序如下：
  1. Clear["Global`*"];
  2. Array[a, 20];
  3. ss = {};     (* 所有的方案数列表 *)
  4. a = Permutations[{"黄", "绿", "红", "红",
  5.    "红"}, {5}]; (* 5个有重复元素的全排列，a 是个列表*)
  6. L = Length[a];       (* 共有多少种线排列？ *)
  7. (* %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% *)
  8. s = a[[1]];  (* 候选方案*)
  9. ss = Append[ss, s];
  10. s1 = Reverse[s];  (* 候选方案反排*)
  11. Do[If[a[[i]] == s || a[[i]] == s1, a[[i]] = {}], {i, 2,
  12.   L}]; (* s 左移，s1右移之前，先筛一次 *)
  13. Do[s = RotateLeft[s];
  14. s1 = RotateRight[s1]; (* s 左移一位，并存到 s 中; s1右移一位，并存到 s1 中*)
  15. Do[If[a[[i]] == s || a[[i]] == s1, a[[i]] = {}], {i, 2, L}];
  16. , {i, 1,
  17.   4}];     (* s每左移一位、s1每右移一位，与其余的比较，若有一个是相同的，将那个其余清空。共筛 4 次 *)
  18. a = DeleteCases[a, {}]; (* 去掉 a 中的所有空集 *)
  19. a = Delete[a, 1]    (* 去掉 a 中的候选方案 a[[1]] 后的 a 列表 *)
  20. L = Length[a]       (* 筛一轮后的 a 还有多少种线排列？ *)
  21. If[L == 0, Print[ss, " 所有方案展示"]];
  22. Print[" ########################################## "];
  23. s = a[[1]];  (* 候选方案*)
  24. ss = Append[ss, s];
  25. s1 = Reverse[s];  (* 候选方案反排*)
  26. Do[If[a[[i]] == s || a[[i]] == s1, a[[i]] = {}], {i, 2,
  27.   L}]; (* s 左移，s1右移之前，先筛一次 *)
  28. Do[s = RotateLeft[s];
  29. s1 = RotateRight[s1]; (* s 左移一位，并存到 s 中; s1右移一位，并存到 s1 中*)
  30. Do[If[a[[i]] == s || a[[i]] == s1, a[[i]] = {}], {i, 2, L}];
  31. , {i, 1,
  32.   4}];     (* s每左移一位、s1每右移一位，与其余的比较，若有一个是相同的，将那个其余清空。共筛 4 次 *)
  33. a = DeleteCases[a, {}]; (* 去掉 a 中的所有空集 *)
  34. a = Delete[a, 1]    (* 去掉 a 中的候选方案 a[[1]] 后的 a 列表 *)
  35. L = Length[a]       (* 筛一轮后的 a 还有多少种线排列？ *)
  36. If[L == 0, Print[ss, " 所有方案展示"]];
  37. Print[" ########################################## "];
复制代码


上面这程序运行结果为：

运行结果.png

上面程序尚存在毛病，因为有两段相邻程序是完全相同的，必须把它们放进一个 While 循环语句中去以控制循环次数才行。试改如下：
  1. Clear["Global`*"];
  2. Array[a, 20];
  3. ss = {};     (* 所有的方案数列表 *)
  4. a = Permutations[{"黄", "绿", "红", "红",
  5.    "红"}, {5}]; (* 5个有重复元素的全排列，a 是个列表*)
  6. L = Length[a];       (* 共有多少种线排列？ *)
  7. (* %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% *)
  8. While[L > 0,
  9. s = a[[1]];  (* 候选方案*)
  10. ss = Append[ss, s];
  11. s1 = Reverse[s];  (* 候选方案反排*)
  12. Do[If[a[[i]] == s || a[[i]] == s1, a[[i]] = {}], {i, 2,
  13.    L}]; (* s 左移，s1右移之前，先筛一次 *)
  14. Do[s = RotateLeft[s]; s1 = RotateRight[s1]; (* s 左移一位，并存到 s 中;
  15.   s1右移一位，并存到 s1 中*)
  16.   Do[If[a[[i]] == s || a[[i]] == s1, a[[i]] = {}], {i, 2, L}];
  17.   , {i, 1, 4}];     (* s每左移一位、s1每右移一位，与其余的比较，若有一个是相同的，将那个其余清空。共筛 4 次 *)
  18. a = DeleteCases[a, {}]; (* 去掉 a 中的所有空集 *)
  19. a = Delete[a, 1]    (* 去掉 a 中的候选方案 a[[1]] 后的 a 列表 *)
  20.     L = Length[a]       (* 筛一轮后的 a 还有多少种线排列？ *)
  21.     If[L == 0, Print[ss, " 所有方案展示"]];
  22. Print[" ########################################## "];
  23. ]
复制代码


上面这样改动以后程序不能运行。不知应当如何改才行？

补充内容 (2021-7-8 12:03):
程序中第 2 行的 Array[a, 20]; 无用，应该去掉。

补充内容 (2021-7-9 08:54):
上面加入 While 循环语句后程序出错，问题是 While 循环内的所有语句后必须用分号才行。改正后的程序见下页。
毋因群疑而阻独见　　毋任己意而废人言
毋私小惠而伤大体　　毋借公论以快私情
回复 支持 反对

使用道具 举报

TSC999
 楼主| 发表于 2021-7-8 23:18:54 | 显示全部楼层
本帖最后由 TSC999 于 2021-7-9 09:11 编辑

下面是用改正错误后的程序进行计算，并与常新德公式计算结果对比。有时二者完全相同，但有时二者不一样，需要判定是哪个有错。例如下面的例子：

下面是四色珠子，黄色 1 颗、蓝色 1 颗、绿色 2 颗、红色 3 颗。手串共由这 7 颗珠子穿成。

按程序计算，共有 30 种花色如下图所示。但是按照常新德的公式计算，却有 31 种花色。问题来了，是公式错了还是程序错了？

4-1123的花色数.png

上图中有没有花色重复的？ 有没有遗漏的？

下面是程序计算和常新德公式计算，程序代码放在一起了。
有个疑问，公式计算中，算出了有 2 个圆排列是对称的，结果就折算成了 1 个环排列。我咋看不出哪个环排列是对称的？

  1. Clear["Global`*"];   
  2. m = 4; n[1] = 1; n[2] = 1; n[3] = 2; n[4] = 3;
  3. Subscript[S, n] = \!\(
  4. \*UnderoverscriptBox[\(\[Sum]\), \(i = 1\), \(m\)]\(n[i]\)\);
  5. ss = {};     (* 所有的方案数列表 *)
  6. a = Permutations[{"黄", "蓝", "绿", "绿", "红", "红", "红"}, {Subscript[S,
  7.    n]}]; (* Subscript[S, n] 个有重复元素的全排列 *)
  8. L = Length[a];       (* 共有多少种线排列？ *)
  9. k = 0;
  10. While[L > 0,
  11.   s = a[[1]];  (* 候选方案*)
  12.   ss = Append[ss, s];
  13.   s1 = Reverse[s];  (* 候选方案反排*)
  14.   Do[If[a[[i]] == s || a[[i]] == s1, a[[i]] = {}], {i, 2, L}]; (*
  15.   s 左移，s1右移之前，先筛一次 *)
  16.   Do[s = RotateLeft[s]; s1 = RotateRight[s1]; (* s 左移一位，并存到 s 中;
  17.    s1右移一位，并存到 s1 中*)
  18.    Do[If[a[[i]] == s || a[[i]] == s1, a[[i]] = {}], {i, 2, L}];
  19.    , {i, 1, Subscript[S, n] - 1}];     (*
  20.   s每左移一位、s1每右移一位，与其余的比较，若有一个是相同的，将那个其余清空。共筛 Subscript[S, n] 次 *)
  21.   a = DeleteCases[a, {}]; (* 去掉 a 中的所有空集 *)
  22.   a = Delete[a, 1];    (* 去掉 a 中的候选方案 a[[1]] 后的 a 列表 *)
  23.   L = Length[a];       (* 筛一轮后的 a 还有多少种线排列？ *)
  24.   k = k + 1;
  25.   If[L == 0, Print[ss, " 所有花色方案展示，方案数 = ", k]];
  26.   ];
  27. (*以下是按常新德公式计算*)
  28. Q = Sum[EulerPhi[d] *(Subscript[S, n]/d)!/\!\(
  29. \*UnderoverscriptBox[\(\[Product]\), \(i = 1\), \(m\)]\(\((
  30. \*FractionBox[\(n[i]\), \(d\)])\)!\)\), {d,
  31.    Divisors[GCD[n[1], n[2], n[3], n[4]]]}]/Subscript[S, n](*圆排列数*)
  32. M = (\!\(
  33. \*UnderoverscriptBox[\(\[Sum]\), \(i = 1\), \(m\)]\(\[LeftFloor]
  34. \*FractionBox[\(n[i]\), \(2\)]\[RightFloor]\)\))!/\!\(
  35. \*UnderoverscriptBox[\(\[Product]\), \(i = 1\), \(m\)]\(\[LeftFloor]
  36. \*FractionBox[\(n[i]\), \(2\)]\[RightFloor]!\)\)(*圆排列中的对称排列数*)
  37. \[CapitalPhi] = (Q + M)/2(*环排列数*)

复制代码


上面程序运行结果是： 程序算出环排列数为 30，它们的具体排列方案见上图。常新德公式计算圆排列数为 Q = 60 种，其中对称排列的为  M = 2 种，所以环排列数  Φ =(Q+M)/2 = 31 种，比程序算的多了一种。

我看不出来存在 2 种对称的圆排列，如果有，它是什么模样的？ 黄珠 1 颗、蓝珠 1 颗、绿珠 2 颗、红珠 3 颗。它们的圆排列咋能有对称的呢？ 哪位网友发现有对称的，请告知一下。

补充内容 (2021-7-15 08:57):
最终发现程序没错，常新德公式也没错，错在我马虎了，没有认真看常新德老师的论文。各色珠子个数有奇有偶，若奇数个数大于 2 则 M=0，不存在对称圆排列，不用按公式计算了。当奇数个数是0、1、2 时才按公式计算。
毋因群疑而阻独见　　毋任己意而废人言
毋私小惠而伤大体　　毋借公论以快私情
回复 支持 反对

使用道具 举报

TSC999
 楼主| 发表于 2021-7-14 21:35:26 | 显示全部楼层
本帖最后由 TSC999 于 2021-7-15 09:13 编辑

今天这个帖子的问题可以彻底结束了。经编程试验知：

m = 4; n[1] = 1; n[2] = 1; n[3] = 1;  n[4] = 3  时，环排列数为 10 种,  公式算为 10.5 种。公式算的对称圆排列为 1个，实际应当是 0 个。
m = 4; n[1] = 1; n[2] = 1; n[3] = 2;  n[4] = 3  时，环排列数为 30 种， 公式算为 31 种。公式算的对称圆排列为 2个， 实际应当是 0 个。
m = 4; n[1] = 1; n[2] = 1; n[3] = 1;  n[4] = 2  时，环排列数为  6 种,  公式算为 6.5 种。公式算的对称圆排列为 1个， 实际应当是 0 个。
m = 4; n[1] = 1; n[2] = 3; n[3] = 3;  n[4] = 3  时，环排列数为 840 种, 公式算为 843 种。公式算的对称圆排列为 6个，实际应当是 0 个。
m = 3; n[1] = 1; n[2] = 1; n[3] = 3  时，环排列数为 2 种, 公式算为 2.5 种。公式算的对称圆排列为 1个，实际应当是 0 个。
m = 3; n[1] = 3; n[2] = 3; n[3] = 5  时，环排列数为 420 种, 公式算为 426 种。公式算的对称圆排列为 12个，实际应当是 0 个。
m = 3; n[1] = 1; n[2] = 1; n[3] = 1  时，环排列数为 1 种, 公式算为 1.5 种。公式算的对称圆排列为 1个，实际应当是 0 个。
m = 3; n[1] = 3; n[2] = 3; n[3] = 3  时，环排列数为 94 种, 公式算为 97 种。公式算的对称圆排列为 6个，实际应当是 0 个。
m = 5; n[1] = 1; n[2] = 1; n[3] = 1; n[4] = 2; n[5] = 2 时环排列数为 90 种, 公式算为 91 种。公式算的对称圆排列为 2个，实际应当是 0 个。
m = 5; n[1] = 1; n[2] = 1; n[3] = 1; n[4] = 2; n[5] = 3 时环排列数为 210 种, 公式算为 211 种。公式算的对称圆排列为 2个，实际应当是 0 个。
m = 5; n[1] = 1; n[2] = 1; n[3] = 2; n[4] = 2; n[5] = 3  时环排列数为 840 种, 公式算为 843 种。公式算的对称圆排列为 6个，实际应当是 0 个。
m = 5; n[1] = 1; n[2] = 1; n[3] = 1; n[4] = 2; n[5] = 2  时环排列数为 90 种, 公式算为 91 种。公式算的对称圆排列为 2个，实际应当是 0 个。

这就说明，当各种颜色的珠子个数有奇有偶，而奇数个数多于两个时，对称圆排列是没有的，即此时 M=0，此时环排列的数目等于圆排列数目的一半。

而当奇数个数为 0、1、2 时，M 不等于 0，其值需要按公式计算，此时环排列的数目等于圆排列数目的一半再加上 M 的一半。

再回头看看常新德老师的论文，才发现人家已经把这个问题说明白了，而且论证了为什么奇数个数多于两个时，对称圆排列是不存的。见下图：

奇数个数超过 2 个则对称圆排列数为零.png

这就对了，主帖提出的疑问是不存在的，常新德的公式是完全正确的。

为什么奇数个数多于两个时，对称圆排列不存在，见原著中的证明：

证明.png

折腾了好几天，最终证明是程序没有错，常新德公式也没有错。错在本人马虎了，没有认真阅读常新德老师的那篇论文。只是跑马观花地瞄了一眼。论文本身也有一点点小瑕疵，
如果多说一句话就好了——当奇数个数大于等于 3 时 M=0，此时按公式算出的 M 值不能用。小于等于 2 时才能按公式算 M。




毋因群疑而阻独见　　毋任己意而废人言
毋私小惠而伤大体　　毋借公论以快私情
回复 支持 反对

使用道具 举报

TSC999
 楼主| 发表于 2021-7-4 23:25:17 | 显示全部楼层
为什么《 数学研究》 网站现在发不了图片呢？我前不久还能发呢。如果是我的电脑有了问题，为什么我能在《 数学中国》 网站发图片，在《初等数学讨论》 网站也能发图片？

在这个网站发图片时，点击 “图片”，出不来 “选择图片” 的提示。但是以前可以。

点评

TSC999
由360安全游览器换成了 360 急速游览器，能发图了。谢谢 gxqcn 站长！  发表于 2021-7-5 17:37
gxqcn
再换一款浏览器试试  发表于 2021-7-5 13:09
TSC999
去掉右上角“纯文本” 的勾，也不行。右上角的 “常用” 改 “高级”，仍不行。  发表于 2021-7-5 08:24
gxqcn
请把右上角的“纯文本”勾选项取消，切换成“所见即所得模式”看看  发表于 2021-7-5 07:52
毋因群疑而阻独见　　毋任己意而废人言
毋私小惠而伤大体　　毋借公论以快私情
回复 支持 反对

使用道具 举报

TSC999
 楼主| 发表于 2021-7-5 09:01:43 | 显示全部楼层
本帖最后由 TSC999 于 2021-7-5 09:28 编辑

题目：黄、绿、红三种颜色的彩色珠子，黄珠 4 个，绿珠 4 个， 红珠 1 个。用它们穿成 9 个珠子的手串，有几种穿法？

从常新德老师的论文，按以下公式算出环排列数为 38。

圆排列数为 70，其中对称排列的有 6 个。

  1. Clear["Global`*"];  
  2. m = 3; n[1] = 4; n[2] = 4; n[3] = 1; Subscript[S, n] = \!\(
  3. \*UnderoverscriptBox[\(\[Sum]\), \(i = 1\), \(m\)]\(n[i]\)\);
  4. Q = Sum[EulerPhi[d] *(Subscript[S, n]/d)!/\!\(
  5. \*UnderoverscriptBox[\(\[Product]\), \(i = 1\), \(m\)]\(\((
  6. \*FractionBox[\(n[i]\), \(d\)])\)!\)\), {d,
  7.    Divisors[GCD[n[1], n[2], n[3]]]}]/Subscript[S, n](*圆排列数*)

  9. M = (\!\(
  10. \*UnderoverscriptBox[\(\[Sum]\), \(i = 1\), \(m\)]\(\[LeftFloor]
  11. \*FractionBox[\(n[i]\), \(2\)]\[RightFloor]\)\))!/\!\(
  12. \*UnderoverscriptBox[\(\[Product]\), \(i = 1\), \(m\)]\(\[LeftFloor]
  13. \*FractionBox[\(n[i]\), \(2\)]\[RightFloor]!\)\)(*圆排列中的对称排列数*)
  14. \[CapitalPhi] = (Q + M)/2(*环排列数*)
复制代码

补充内容 (2021-7-9 09:09):
程序计算结果也是 38 种，与常新德公式的计算结果完全相同。
毋因群疑而阻独见　　毋任己意而废人言
毋私小惠而伤大体　　毋借公论以快私情
回复 支持 反对

使用道具 举报

TSC999
 楼主| 发表于 2021-7-5 09:21:48 | 显示全部楼层
本帖最后由 TSC999 于 2021-7-5 09:35 编辑

如果上面的公式正确，计算结果也对。下面改一下参数： 仍是黄、绿、红三种颜色，黄珠 3 个，绿珠 1 个， 红珠 1 个。用它们穿成 5 个珠子的手串，有几种穿法？

仍用上面的程序，计算结果是 5/2 个。手工计算是  2 个。咋办？ 是否最后那个公式应该改为取整？

为什么会出现这样的情况呢？ 因为常新德论文的定理 6 中说，各种颜色的珠子数目，至多只能有两个奇数。现在是黄珠 3 个，绿珠 1 个， 红珠 1 个，三个都是奇数，所以就出了点问题。或者说这个定理 6 尚不够完善吧？

  1. Clear["Global`*"];  
  2. m = 3; n[1] = 3; n[2] = 1; n[3] = 1; Subscript[S, n] = \!\(
  3. \*UnderoverscriptBox[\(\[Sum]\), \(i = 1\), \(m\)]\(n[i]\)\);
  4. Q = Sum[EulerPhi[d] *(Subscript[S, n]/d)!/\!\(
  5. \*UnderoverscriptBox[\(\[Product]\), \(i = 1\), \(m\)]\(\((
  6. \*FractionBox[\(n[i]\), \(d\)])\)!\)\), {d,
  7.        Divisors[GCD[n[1], n[2], n[3]]]}]/Subscript[S, n](*圆排列数*)

  9. M = (\!\(
  10. \*UnderoverscriptBox[\(\[Sum]\), \(i = 1\), \(m\)]\(\[LeftFloor]
  11. \*FractionBox[\(n[i]\), \(2\)]\[RightFloor]\)\))!/\!\(
  12. \*UnderoverscriptBox[\(\[Product]\), \(i = 1\), \(m\)]\(\[LeftFloor]
  13. \*FractionBox[\(n[i]\), \(2\)]\[RightFloor]!\)\)(*圆排列中的对称排列数*)
  14. \[CapitalPhi] = (Q + M)/2      (*环排列数*)
复制代码


程序运行结果是  Q=4,   M=1,  Φ=(Q+M)/2=(4+1)/2=5/2。
毋因群疑而阻独见　　毋任己意而废人言
毋私小惠而伤大体　　毋借公论以快私情
回复 支持 反对

使用道具 举报

TSC999
 楼主| 发表于 2021-7-5 13:13:08 | 显示全部楼层
当 \( m=3,  n (i) =3, 5, 9 \) 时，结果也是分数 \( 80185/2 \)。 当 \( m=4,  n(i)=3, 1, 1, 1 \) 时，结果也是分数 \( 21/2 \)。例子太多了。
需要编写一个程序，计算环排列的准确值。以便修正常新德的公式。常老师后来好像与另外一个人合写了新的论文，不知道他在新论文中是否对自己原先的公式做了修正。

补充内容 (2021-7-9 09:20):
常新德老师另有一篇类似论文发在网上，是跟别人合著的，那人的名字还在常老师前面写着。我没看这篇，因为它收费。我并非没有钱付费看，凭什么看科技论文还要收费？如果收的钱给了作者还行，那我肯定愿意付费。
毋因群疑而阻独见　　毋任己意而废人言
毋私小惠而伤大体　　毋借公论以快私情
回复 支持 反对

使用道具 举报

TSC999
 楼主| 发表于 2021-7-5 17:33:58 | 显示全部楼层
本帖最后由 TSC999 于 2021-7-5 17:42 编辑

举一个例子，有 n = 8 颗珠子，珠子颜色 m = 2，比如黄色和红色。则按本帖题目内容，共有 30 种花色组合，

如果这 30 种组合细分，就需要按常新德的公式分别计算各种情况：

     8 黄是 1 种，8 红也是 1 种，共 2 种。
     7 黄 1 红是 1 种，1 黄 7 红也是 1 种，共 2 种。
     2 黄 6 红是 4 种，6 黄 2 红也是 4 种，共 8 种。
     3 黄 5 红是 5 种，5 黄 3 红也是 5 种，共 10 种。
     4  黄 4 红是 8 种。

所以共有 2 + 2 + 8 + 10 + 8 = 30 种。具体花色如下图：

2 色 8 珠的组合图案展示.png

换了一个游览器，原先是用 360 安全游览器，不知出了什么毛病，不能发图了。按照本站站长 gxqcn 的指导，换为 360 极速游览器，能发图了。谢谢 gxqcn 站长！

补充内容 (2021-7-9 09:22):
这一页是换了游览以后试试能不能发图。别无深意。
毋因群疑而阻独见　　毋任己意而废人言
毋私小惠而伤大体　　毋借公论以快私情
回复 支持 反对

使用道具 举报

TSC999
 楼主| 发表于 2021-7-7 23:35:45 | 显示全部楼层
本帖最后由 TSC999 于 2021-7-7 23:42 编辑

上面程序的编程思路见程序中的注释，这里补充说明一下。
由黄、绿、红、红、红这 5 个有重复的元素排成一条线，共有 20 种情况。可从中任选一种例如 “黄 绿 红 红 红” 作为一种手串花色方案的样本。可将它想像为下面的手串：

                                    黄
                               绿        红
                                  红  红
                                                      
   将其顺时针旋转一颗珠子，从最高点逆时针方向数就是 “绿 红 红 红 黄” 的线排列，从其余线排列中把这种排列划掉。再顺时针旋转一颗珠子，再与剩余线排列逐个比较，划掉相同者。如此旋转 4 次，比较 4 次，就能筛去一部分相同的圆排列。
把上述样本方案 “黄 绿 红 红 红” 反向排列成 “红 红 红 绿 黄”，与剩余线排列逐个比较一次，划掉相同者。然后再顺时针旋转 4 次并每次与剩余线排列比较，划掉相同者。如此筛选一轮，除去划掉的，就只剩下 10 个线排列了。
从这 10 个线排列中再随便抽取一个，进行又一轮同样的操作，如此进行下去，直到剩余的线排列全部消灭、一个不剩为止。此时那些抽取的样本的集合，就是花色组合数目了。

补充内容 (2021-7-9 09:26):
本页是对下页的编程思路作了一些说明。
毋因群疑而阻独见　　毋任己意而废人言
毋私小惠而伤大体　　毋借公论以快私情
回复 支持 反对

使用道具 举报

TSC999
 楼主| 发表于 2021-7-8 17:30:36 | 显示全部楼层
本帖最后由 TSC999 于 2021-7-8 19:38 编辑

问题解决了！While  循环中的每条语句结尾必须是分号。改后的程序如下：

  1. Clear["Global`*"];
  2. ss = {};     (* 所有的方案数列表 *)
  3. a = Permutations[{"黄", "绿", "红", "红",
  4.     "红"}, {5}]; (* 5个有重复元素的全排列，a 是个列表*)
  5. L = Length[a];       (* 共有多少种线排列？ *)
  6. k = 0;
  7. While[L > 0,
  8.   s = a[[1]];  (* 候选方案*)
  9.   ss = Append[ss, s];
  10.   s1 = Reverse[s];  (* 候选方案反排*)
  11.   Do[If[a[[i]] == s || a[[i]] == s1, a[[i]] = {}], {i, 2, L}]; (*
  12.   s 左移，s1右移之前，先筛一次 *)
  13.   Do[s = RotateLeft[s]; s1 = RotateRight[s1]; (* s 左移一位，并存到 s 中;
  14.    s1右移一位，并存到 s1 中*)
  15.    Do[If[a[[i]] == s || a[[i]] == s1, a[[i]] = {}], {i, 2, L}];
  16.    , {i, 1, 4}];     (*
  17.   s每左移一位、s1每右移一位，与其余的比较，若有一个是相同的，将那个其余清空。共筛 4 次 *)
  18.   a = DeleteCases[a, {}]; (* 去掉 a 中的所有空集 *)
  19.   a = Delete[a, 1];    (* 去掉 a 中的候选方案 a[[1]] 后的 a 列表 *)
  20.   Print[a];
  21.   L = Length[a];       (* 筛一轮后的 a 还有多少种线排列？ *)
  22.   Print["L= ", L];
  23.   If[L == 0, Print[ss, " 所有方案展示"]];
  24.   k = k + 1;
  25.   Print["以上为第 ", k, " 轮筛选结果。"];
  26.   Print[""];
  27.   ];
复制代码


运行结果是：

运行结果.png
毋因群疑而阻独见　　毋任己意而废人言
毋私小惠而伤大体　　毋借公论以快私情
回复 支持 反对

使用道具 举报

TSC999
 楼主| 发表于 2021-7-8 19:36:54 | 显示全部楼层
下面是 4 种颜色、每种颜色的珠子个数分别为 1、1、1、3， 手串珠子个数为 1+1+1+3 = 6 的花色方案数计算程序：

  1. Clear["Global`*"];   
  2. m = 4; n[1] = 1; n[2] = 1; n[3] = 1;
  3. n[4] = 3; (* m=4;n[1]=1;n[2]=1;n[3]=1;n[4]=3; 环排列数 \[CapitalPhi]=\
  4. \[LeftFloor]21/2\[RightFloor]=10 *)
  5. Subscript[S, n] = \!\(
  6. \*UnderoverscriptBox[\(\[Sum]\), \(i = 1\), \(m\)]\(n[i]\)\);
  7. ss = {};     (* 所有的方案数列表 *)
  8. a = Permutations[{"黄", "绿", "蓝", "红", "红", "红"}, {Subscript[S,
  9.    n]}]; (* Subscript[S, n] 个有重复元素的全排列，a 是个列表*)
  10. L = Length[a];       (* 共有多少种线排列？ *)
  11. k = 0;
  12. While[L > 0,
  13.   s = a[[1]];  (* 候选方案*)
  14.   ss = Append[ss, s];
  15.   s1 = Reverse[s];  (* 候选方案反排*)
  16.   Do[If[a[[i]] == s || a[[i]] == s1, a[[i]] = {}], {i, 2, L}]; (*
  17.   s 左移，s1右移之前，先筛一次 *)
  18.   Do[s = RotateLeft[s]; s1 = RotateRight[s1]; (* s 左移一位，并存到 s 中;
  19.    s1右移一位，并存到 s1 中*)
  20.    Do[If[a[[i]] == s || a[[i]] == s1, a[[i]] = {}], {i, 2, L}];
  21.    , {i, 1, Subscript[S, n] - 1}];     (*
  22.   s每左移一位、s1每右移一位，与其余的比较，若有一个是相同的，将那个其余清空。共筛 Subscript[S, n] 次 *)
  23.   a = DeleteCases[a, {}]; (* 去掉 a 中的所有空集 *)
  24.   a = Delete[a, 1];    (* 去掉 a 中的候选方案 a[[1]] 后的 a 列表 *)
  25.   L = Length[a];       (* 筛一轮后的 a 还有多少种线排列？ *)
  26.   k = k + 1;
  27.   If[L == 0, Print[ss, " 所有花色方案展示，方案数 = ", k]];
  28.   ];
复制代码


程序运行结果为：

4 色 6 珠.png

用常新德的公式计算结果是个分数  21/2，如果取整等于 10，与程序计算结果相同。
毋因群疑而阻独见　　毋任己意而废人言
毋私小惠而伤大体　　毋借公论以快私情
回复 支持 反对

使用道具 举报

12下一页
返回列表 发新帖
高级模式
B Color Image Link Quote Code Smilies
您需要登录后才可以回帖 登录 | 欢迎注册

本版积分规则

小黑屋|手机版|数学研发网 ( 苏ICP备07505100号 )

GMT+8, 2024-4-24 18:20 , Processed in 0.053756 second(s), 23 queries .

Powered by Discuz! X3.5

© 2001-2024 Discuz! Team.

快速回复 返回顶部 返回列表