三角形内角和定理的另类证明

dlsh

\(\frac{\overrightarrow{AC}}{\overrightarrow{AB}}\frac{\overrightarrow{BA}}{\overrightarrow{BC}}\frac{\overrightarrow{BC}}{\overrightarrow{AC}}=\frac{AC}{AB}e^{iA}\frac{BA}{BC}e^{iB}\frac{BC}{AC}e^{iC}=-1\)
所以A+B+C=π

向量商

creasson

可以用它证明正弦定理和余弦定理，你试试。

dlsh

证明：\(假设B在原点 ，C在实轴上，\frac{\overrightarrow{AC}}{\overrightarrow{AB}}=\lambda v,其中\frac{AC}{AB}=\lambda,v=e^i{A}，根据向量定比分点公式得a=\frac{1}{1-\lambda v}，\bar{a}=\frac{v}{v-\lambda}\)
余弦定理
\(AB^2+AC^2-BC^2=a\bar {a}+(a-c)(\bar {a}-\bar {c})-(b-c)(\bar {b}-\bar {c})=\left(\frac{1}{1-\lambda v}\frac{v}{v-\lambda}\right)+\frac{\lambda v}{1-\lambda v}\frac{\lambda}{v-\lambda}-1=\frac{\lambda(1+v^2)}{(1-\lambda v)\left(v-\lambda\right)}\)
\(2ABACcosA=|\frac{1}{1-\lambda v}\frac{\lambda v}{v-\lambda}(v+\frac{1}{v})|=\frac{\lambda(1+v^2)}{(1-\lambda v)\left(v-\lambda\right)}\)
正弦定理
\(\frac{BC}{sinA}=|\frac{1}{\frac{v-\bar v}{2}}i|=\frac{2}{1-v^2},因为∠O=2∠A，由向量定比分点公式得o=\frac{1}{1-v^2},还可以证明OA=OB=OC\)

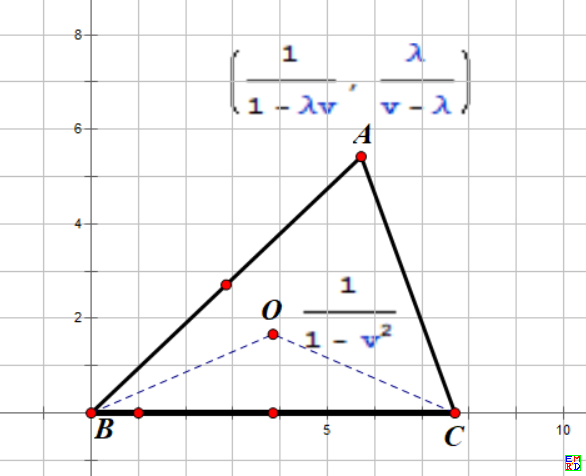
老师如何证明






补充内容 (2021-7-18 22:38):
\(\frac{BC}{sinA的计算结果应该加绝对值符号\)