4x3矩阵列空间的基 和. 其左零空间的基，是否可以张成整个四维空间？

jiewenji

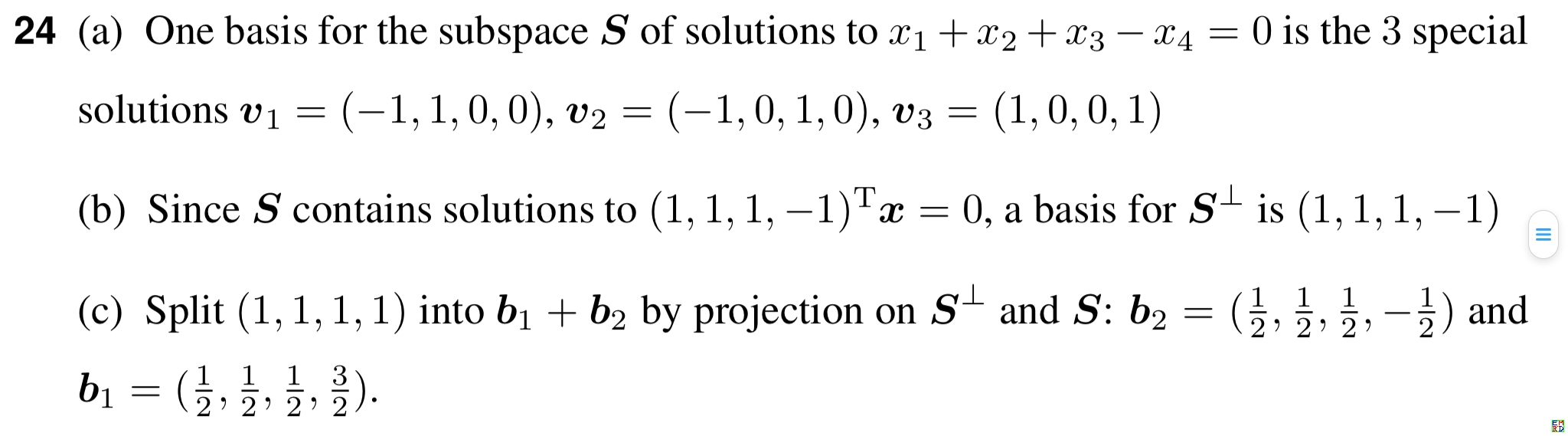
我对上图的问题和答案没有任何疑议。我自己的问题来自于题目的第三问。当我看到第三问答案的时候，我想这个答案是通过什么方法得到的呢？答案应该不唯一吧？

第一问的答案给出了S的三个独立的列向量，第二问给出了左零空间的基向量。S的列空间和左零空间是正交补，也就是说四维空间的向量要么在S的列空间中，要么在S的左零空间中。b=(1,1,1,1)也不例外。那么只要b和左零空间基向量不共线，那么用b减去b2=(1, 1, 1, -1)，得到的b1就一定在S空间中！b-b2=(0,0,0,2)，可是这个得到的向量明显不在S的列空间中。所以是不是上方红字部分的结论是错误的？第三问应该用什么办法求解呢？