- 注册时间
- 2007-12-27
- 最后登录
- 1970-1-1
- 威望
- 星
- 金币
- 枚
- 贡献
- 分
- 经验
- 点
- 鲜花
- 朵
- 魅力
- 点
- 上传
- 次
- 下载
- 次
- 积分
- 49497
- 在线时间
- 小时
|
楼主 |
发表于 2021-11-5 07:41:44
|
显示全部楼层
所以我们现在只需要考虑最多两个$d_h$非边界值的情况。正好两个非边界值情况分四种
1. $n-1 \gt d_1 \gt d_2 \gt 0, 0=I_0\lt i_1 \lt I_2=n$
2. $n-1=D_1 \gt d_2 \gt d_3 \gt 0, 0=I_0\lt i_1 \lt i_2 \lt I_3=n$
3. $n-1 \gt d_1 \gt d_2 \gt D_3=0, 0=I_0\lt i_1 \lt i_2 \lt I_3=n$
4. $n-1=D_1 \gt d_2 \gt d_3 \gt D_4=0, 0=I_0\lt i_1 \lt i_2 \lt i_3 \lt I_4=n$
根据12#的分析,
第一种情况取极值要求$i_1=\frac n 2$,
计算得出对应方程\(\Delta d^2 +n \Delta d -\frac{8e(n(n-1)-2e)}{n^2}=0\)的正根,这时目标函数取值$\frac {16e^2+n^2\Delta d^2}{4n}$
对应题目中参数可以得出这个极值点取值为250343.166<300000
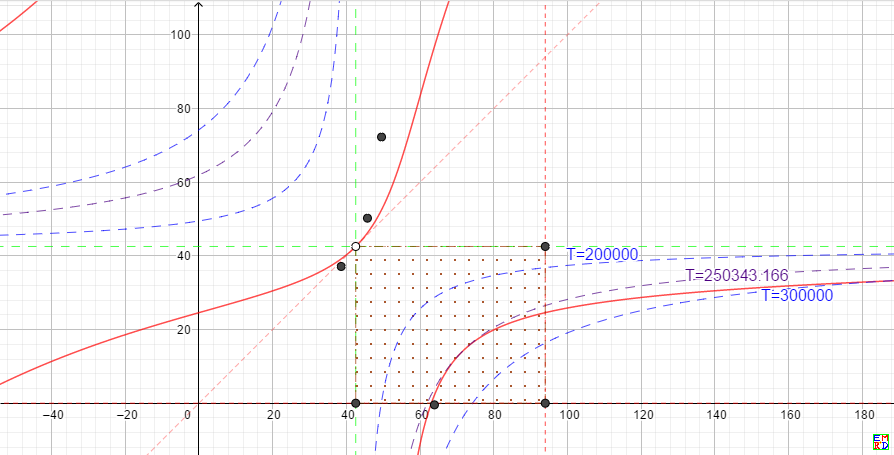
这种情况由于只有三个参数$i_1,d_1,d_2$,我们也可以根据第一个线性约束消去$i_1$,然后根据第二式做出$d_1,d_2$的关系图,如上图中红色曲线,横坐标为$d_1$,纵坐标为$d_2$, 图中直线$d_1\gt d_2, d_1 \lt 94, d_2 \gt 0$给出了$d_1,d_2$的约束,而另外$0\lt i_1\lt 95$对应两条绿色虚直线。
也就是红色曲线落在带点标记的矩形内部部分才是合法的定义域。然后图中分别出目标函数取值为200000,250343.166,300000对应的图,可以看到250343.166正好和红色曲线相切,这时取到的实际是局部最小值而不是最大值。使用拉格朗日乘数法的一个缺点是很难判断这个点是局部最大还是局部最小值。
第二种要求\(\begin{cases}D_1-d_2=d_2-d_3=\Delta d\\I_3-i_2=i_2-i_1=\Delta i\end{cases}\)
可以得到\(\begin{cases}\Delta i\Delta d=\frac{n(n-1)-2e}3\\\Delta i^2-\frac35\Delta i-\frac{n(n-1)-2e}3=0\end{cases}\)
对应题目中参数可以得到极值点取值为\(
\frac53 (n(n-1)-2e)\Delta d-n(n-1)^2+4e(n-1)=\)246881.293<300000
第三种要求\(\begin{cases}d_1-d_2=d_2-D_3=\Delta d\\i_2-i_1=i_1-I_0=\Delta i\end{cases}\)
可以得到\(\begin{cases}\Delta i\Delta d=\frac{2e}3\\\Delta i-\Delta d=\frac35\end{cases}\)
对应结果\(\frac{10e\Delta d}3=\)245263.611<300000
第四种要求\(\begin{cases}D_1-d_2=d_2-d_3=d_3-D_4=\Delta D=\frac{D_1-D_4}3\\i_2-i_1=i_3-i_2=\Delta i\end{cases}\)
可以得到\(\begin{cases}i_2=\frac{2e}{n-1}\\3(n-1)^2 \Delta i^2 +2 (n-1)^3 \Delta i -9e(n^2-n-2e)=0\end{cases}\)
目标函数在极值点变为\(2e(n-1)-\frac49(n-1)^2\Delta i=\)246361.698<300000
计算量还是太大了,后面还有一个$d_h$不在边界和所有$d_h$都不在边界的情况.
比如$ n-1 \gt d_1 \gt 0$时,所有点的度数等于$d_1$,无法同时满足俩约束
比如$n-1=D_1\gt d_2 \gt 0, 0=I_0\lt i_1\lt I_2=n$, 两个变量,两个约束方程,直接得出
$d_2= \frac{2e-(n-1)i_1}{n-i_1}$
$i_1^2-(2n-1)i_1+2e=0$, 对应最值259781.511
比如$n-1 \gt d_1 \gt D_2=0, 0=I_0\lt i_1 \lt I_2=n$, 两个变量,两个约束方程,直接得出
$d_1i_1=2e, d_1=i_1-1$, 对应最值254964.070
比如$n-1 =D_1 \gt d_2 \gt D_3=0, 0=I_0 \lt i_1 \lt i_2 \lt I_3=n$, 三个变量,两个约束方程
得出最值取值条件为\(d_2=\frac{D_1+D_3}2=\frac{n-1}2, \Delta i =i_2-i_1 , i_2+i_1 = \frac{4e}{n-1}, \Delta i^2+2(n-1)\Delta i - \frac{16e(n(n-1)-2e)}{(n-1)^2}=0\), 目标函数取值\(4(n-1)^2 (\frac{2e}{n-1}-\frac {\Delta i}2)+(n-1)^2 \Delta i\)。
本题中计算得到$i_1\lt 0$不符合条件,舍去。
而所有$d_h$都不在边界,就是说所有点度数都是n-1和0,只有一个自由变量$i_1$,无法同时满足两个约束条件。
所以得出在约束条件下目标函数取值不超过259781.511<300000
|
|