四条验证i机器证明的高难度定理

dlsh

1  五圆定理 2莫利定理3Lemoine 圆定理4,泰博定理

dlsh

_{五圆定理证明}

设G是△ABC的重心，K是陪位重心，过K作三边的平行线l1，l2，l3(图1)，这种平行线称为勒穆瓦纳平行线。
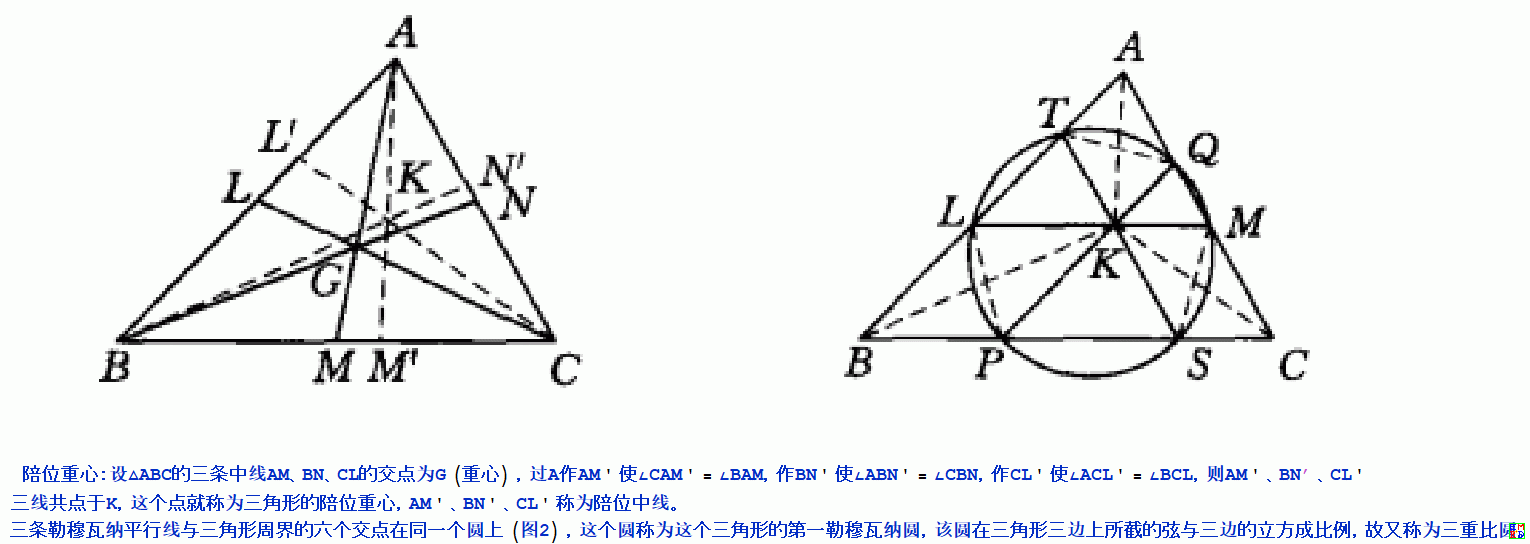三条勒穆瓦纳平行线与三角形周界的六个交点在同一个圆上，这个圆称为这个三角形的第一勒穆瓦纳圆，该圆在三角形三边上所截的弦与三边的立方成比例，故又称为三重比圆。

1. 
   
2. Clear["Global`*"]
   
3. 
   
4. \!\(\*OverscriptBox["a", "_"]\) = 1/a;
   
5. \!\(\*OverscriptBox["b", "_"]\) = 1/b;
   
6. \!\(\*OverscriptBox["c", "_"]\) = 1/c; g = (a + b + c)/3;
   
7. \!\(\*OverscriptBox["g", "_"]\) = (
   
8. \!\(\*OverscriptBox["a", "_"]\) +
   
9. \!\(\*OverscriptBox["b", "_"]\) +
   
10. \!\(\*OverscriptBox["c", "_"]\))/3;
    
11. k[a_, b_] := (a - b)/(
    
12. \!\(\*OverscriptBox["a", "_"]\) -
    
13. \!\(\*OverscriptBox["b", "_"]\));
    
14. \!\(\*OverscriptBox["k", "_"]\)[a_, b_] := 1/k[a, b];(*复斜率定义*)
    
15. k1 = (a^2 b c)/k[g, a]; k2 = (b^2 a c)/k[g, b];
    
16. 
    
17. \!\(\*OverscriptBox["Jd", "_"]\)[k1_, a1_, k2_, a2_] := -((a1 - k1
    
18. \!\(\*OverscriptBox["a1", "_"]\) - (a2 - k2
    
19. \!\(\*OverscriptBox["a2", "_"]\)))/(
    
20.   k1 - k2));(*复斜率等于k1,过点A1与复斜率等于k2,过点A2的直线交点*)
    
21. Jd[k1_, a1_, k2_, a2_] := -((k2 (a1 - k1
    
22. \!\(\*OverscriptBox["a1", "_"]\)) - k1 (a2 - k2
    
23. \!\(\*OverscriptBox["a2", "_"]\)))/(k1 - k2));
    
24. Waixin[a_, b_, c_] := (a
    
25. \!\(\*OverscriptBox["a", "_"]\) (b - c) + b
    
26. \!\(\*OverscriptBox["b", "_"]\) (c - a) + c
    
27. \!\(\*OverscriptBox["c", "_"]\) (a - b) )/(
    
28. \!\(\*OverscriptBox["a", "_"]\) (b - c) +
    
29. \!\(\*OverscriptBox["b", "_"]\) (c - a) +
    
30. \!\(\*OverscriptBox["c", "_"]\) (a - b));
    
31. \!\(\*OverscriptBox["Waixin", "_"]\)[a_, b_, c_] := -((a
    
32. \!\(\*OverscriptBox["a", "_"]\) (
    
33. \!\(\*OverscriptBox["b", "_"]\) -
    
34. \!\(\*OverscriptBox["c", "_"]\)) + b
    
35. \!\(\*OverscriptBox["b", "_"]\) (
    
36. \!\(\*OverscriptBox["c", "_"]\) -
    
37. \!\(\*OverscriptBox["a", "_"]\)) + c
    
38. \!\(\*OverscriptBox["c", "_"]\) (
    
39. \!\(\*OverscriptBox["a", "_"]\) -
    
40. \!\(\*OverscriptBox["b", "_"]\)) )/(
    
41. \!\(\*OverscriptBox["a", "_"]\) (b - c) +
    
42. \!\(\*OverscriptBox["b", "_"]\) (c - a) +
    
43. \!\(\*OverscriptBox["c", "_"]\) (a - b)));
    
44. k = Jd[k1, a, k2, b];
    
45. \!\(\*OverscriptBox["k", "_"]\) =
    
46. \!\(\*OverscriptBox["Jd", "_"]\)[k1, a, k2, b];
    
47. L = Jd[-a b, a, -b c, k];
    
48. \!\(\*OverscriptBox["L", "_"]\) =
    
49. \!\(\*OverscriptBox["Jd", "_"]\)[-a b, a, -b c, k]; t =
    
50. Jd[-a b, a, -a c, k];
    
51. \!\(\*OverscriptBox["t", "_"]\) =
    
52. \!\(\*OverscriptBox["Jd", "_"]\)[-a b, a, -a c, k];
    
53. p = Jd[-a b, k, -b c, b];
    
54. \!\(\*OverscriptBox["p", "_"]\) =
    
55. \!\(\*OverscriptBox["Jd", "_"]\)[-a b, k, -b c, b]; s =
    
56. Jd[-c b, b, -a c, k];
    
57. \!\(\*OverscriptBox["s", "_"]\) =
    
58. \!\(\*OverscriptBox["Jd", "_"]\)[-c b, b, -a c, k];
    
59. o1 = Waixin[t, L, p];
    
60. \!\(\*OverscriptBox["o1", "_"]\) =
    
61. \!\(\*OverscriptBox["Waixin", "_"]\)[t, L, p];
    
62. Simplify[{k,
    
63. \!\(\*OverscriptBox["k", "_"]\)}]
    
64. Simplify[{1, t,
    
65. \!\(\*OverscriptBox["t", "_"]\), , L,
    
66. \!\(\*OverscriptBox[
    
67. RowBox[{"L", "\[IndentingNewLine]"}], "_"]\), , p,
    
68. \!\(\*OverscriptBox["p", "_"]\), , s,
    
69. \!\(\*OverscriptBox["s", "_"]\)}]
    
70. Simplify[{2, o1,
    
71. \!\(\*OverscriptBox["o1", "_"]\), , (o1 - t) (
    
72. \!\(\*OverscriptBox["o1", "_"]\) -
    
73. \!\(\*OverscriptBox["t", "_"]\))}]
    
74. Factor[{2, o1,
    
75. \!\(\*OverscriptBox["o1", "_"]\), , (o1 - t) (
    
76. \!\(\*OverscriptBox["o1", "_"]\) -
    
77. \!\(\*OverscriptBox["t", "_"]\))}]
    
78. Simplify[{3, t - L, s - p, , (t - L)/(s - p)}]
    
79. 
    
80. 
    

复制代码

TSC999

下面用楼主的基本方法证明泰博定理。

1. Clear["Global`*"];  (*三个自由变量 u,v,w，其中 w^2 是 CN 的复斜率 *)
   
2. i0 = 0;
   
3. \!\(\*OverscriptBox[\(i0\), \(_\)]\) = 0;(*三角形ABC的内切圆为单位圆，I0 为内心*)
   
4. a = u - I; b = v - I;  
   
5. \!\(\*OverscriptBox[\(a\), \(_\)]\) = u + I;
   
6. \!\(\*OverscriptBox[\(b\), \(_\)]\) = v + I;
   
7. c = ((u + v) + I (v u - 1))/(u v + 1);
   
8. \!\(\*OverscriptBox[\(c\), \(_\)]\) = ((u + v) - I (v u - 1))/(
   
9. u v + 1);(*采用已知公式：三角形ABC的C点复坐标*)  Print["c = ", c];
   
10. o = ((u - I) (v - I) (I v u + u + v + 3 I))/(4 (u v + 1));  
    
11. \!\(\*OverscriptBox[\(o\), \(_\)]\) = ((u + I) (v + I) (-I u v + u +
    
12.     v - 3 I))/(
    
13. 4 (u v + 1)); (* 采用已知公式：三角形ABC的外接圆圆心O点复坐标*) Print["o = ", o];
    
14. R = -(((1 + u^2) (1 + v^2))/(
    
15.   4 (1 + u v)));  (* 采用已知公式：三角形ABC外接圆的半径 R *)  Print["外接圆半径 R = ", R];
    
16. kf[a_, b_] := (a - b)/(
    
17. \!\(\*OverscriptBox[\(a\), \(_\)]\) -
    
18. \!\(\*OverscriptBox[\(b\), \(_\)]\));
    
19. \!\(\*OverscriptBox[\(kf\), \(_\)]\)[a_, b_] :=
    
20. 1/kf[a, b]; (* AB 直线的复斜率 *)
    
21. (* 以下求角ANC平分线 m 的复斜率, 由于AB的复斜率 kab=1，CN的复斜率 knc=w^2, 所以角平分线的复斜率 km=w  \
    
22. *)
    
23. (* 角ANB平分线 n 与 m 垂直，所以直线 n 的复斜率=-w。另外因直线 KI0//n，故 KI0的复斜率也等于 -w *)
    
24. km = w; kn = -w; kcn = w^2;
    
25. Jd[k1_, a1_, k2_, a2_] := -((k2 (a1 - k1
    
26. \!\(\*OverscriptBox[\(a1\), \(_\)]\)) - k1 (a2 - k2
    
27. \!\(\*OverscriptBox[\(a2\), \(_\)]\)))/(k1 - k2));
    
28. 
    
29. \!\(\*OverscriptBox[\(Jd\), \(_\)]\)[k1_, a1_, k2_, a2_] := -((a1 - k1
    
30. \!\(\*OverscriptBox[\(a1\), \(_\)]\) - (a2 - k2
    
31. \!\(\*OverscriptBox[\(a2\), \(_\)]\)))/(  
    
32.       k1 - k2)); (*复斜率等于k1,过点A1与复斜率等于k2,过点A2的直线交点*)
    
33. n = Simplify@ Jd[kcn, c, 1, a];
    
34. \!\(\*OverscriptBox[\(n\), \(_\)]\) = Simplify@
    
35. \!\(\*OverscriptBox[\(Jd\), \(_\)]\)[kcn, c, 1, a]; Print["n = ", n];
    
36. k = Simplify@ Jd[kn, i0, 1, a];
    
37. \!\(\*OverscriptBox[\(k\), \(_\)]\) = Simplify@
    
38. \!\(\*OverscriptBox[\(Jd\), \(_\)]\)[kn, i0, 1, a]; Print["k = ", k];
    
39. p = Simplify@ Jd[km, i0, 1, a];
    
40. \!\(\*OverscriptBox[\(p\), \(_\)]\) = Simplify@
    
41. \!\(\*OverscriptBox[\(Jd\), \(_\)]\)[km, i0, 1, a]; Print["p = ", p];
    
42. (* 以下求 I1 点的复坐标。它是两直线的交点，一条是复斜率为-1、经过K点的线，另一条是复斜率为 km、经过N点的线 *)
    
43. i1 = Simplify@ Jd[-1, k, km, n];
    
44. \!\(\*OverscriptBox[\(i1\), \(_\)]\) = Simplify@
    
45. \!\(\*OverscriptBox[\(Jd\), \(_\)]\)[-1, k, km,
    
46.    n]; Print["i1 = ", i1];
    
47. (* 以下求 I2 点的复坐标。它是两直线的交点，一条是复斜率为-1、经过P点的线，另一条是复斜率为 kn、经过N点的线 *)
    
48. i2 = Simplify@ Jd[-1, p, kn, n];
    
49. \!\(\*OverscriptBox[\(i2\), \(_\)]\) = Simplify@
    
50. \!\(\*OverscriptBox[\(Jd\), \(_\)]\)[-1, p, kn, n]; Print["i2 = ", i2];
    
51. ki1i0 = Simplify[kf[i1, i0]];
    
52. ki0i2 = Simplify[kf[i2, i0]]; (* 证明 I1、I0、I2 三点共线 *)
    
53. Print["I1I0的复斜率 =", ki1i0]; Print["I0I2的复斜率 =", ki0i2];
    
54. If[ki1i0 == ki0i2,
    
55.   Print["由于 I1I0 的复斜率等于 I0I2 的复斜率，所以 I1、I0、I2 三点共线。"]];
    
56. S[a_, b_] := Sqrt[(a - b) (
    
57. \!\(\*OverscriptBox[\(a\), \(_\)]\) -
    
58. \!\(\*OverscriptBox[\(b\), \(_\)]\))];  (* A、B 点间的距离 *)
    
59. (* 以I1为圆心、I1K为半径作圆I1; 以I2为圆心、I2P为半径作圆I2，则两圆都与BC和CN相切 *)
    
60. (* 以下证明I1圆和I2圆都与O圆相内切 *)
    
61. S1 = Simplify@S[o, i1];   (* I1圆和O圆连心线长度，未简化 *)
    
62. S2 = Simplify@S[o, i2] ; (* I2圆和O圆连心线长度，未简化 *)
    
63. S1 = (-3 w^2 + 10 w + v^2 (w + 1)^2 + u^2 (v^2 + 1) (w + 1)^2 +
    
64.    4 I v (w^2 - 1) + 4 u (w + 1) (I (w - 1) + v (w + 1)) -
    
65.    3)/(-4 (u v + 1) (w + 1)^2); (* 人工协助简化结果 *)
    
66. S2 = (v^2 (w - 1)^2 + u^2 (v^2 + 1) (w - 1)^2 +
    
67.    4 u (v (w - 1) + I (w + 1)) (w - 1) - 3 w^2 - 10 w +
    
68.    4 I v (w^2 - 1) - 3)/(-4 (u v + 1) (w - 1)^2);   (* 人工协助简化结果 *)
    
69. Print["圆O与圆I1连心线长 S1 = ", S1]; Print["圆O与圆I2连心线长 S2 = ", S2];
    
70. R1 = Simplify@S[i1, k] ;  R2 = Simplify@S[i2, p] ;  
    
71. R1 = ((I (w - 1) + u (w + 1)) (I (w - 1) + v (w + 1)))/((u v +
    
72.      1) (w + 1)^2);   (* 人工协助简化结果 *)
    
73. R2 = ((u (w - 1) + I (w + 1)) (v (w - 1) + I (w + 1)))/((u v +
    
74.      1) (w - 1)^2); (* 人工协助简化结果 *)
    
75. Print["I1圆半径 R1 = ", R1]; Print["I2圆半径 R2 = ", R2];
    
76. Print["圆O与圆I1连心线长 + 圆I1半径 = ", Factor[Simplify[S1 + R1]]];
    
77. Print["圆O与圆I2连心线长 + 圆I2半径 = ", Factor[Simplify[S2 + R2]]];
    
78. Print["圆O半径 = ", R];
    
79. If[Factor[Simplify[S1 + R1]] == Factor[Simplify[S2 + R2]] == R,
    
80. Print["由于圆O与圆I1连心线长+圆I1半径 = 圆O与圆I2连心线长+圆I2半径 = 圆O半径，因此 \
    
81. \[CircleDot]I1 和 \[CircleDot]I2 圆都与 \[CircleDot]O 圆相切。"]]
    
82. t1 = Simplify[-((R1 Sqrt[ (i1 - o) (
    
83. \!\(\*OverscriptBox[\(i1\), \(_\)]\) -
    
84. \!\(\*OverscriptBox[\(o\), \(_\)]\))] + i1
    
85. \!\(\*OverscriptBox[\(o\), \(_\)]\) - i1
    
86. \!\(\*OverscriptBox[\(i1\), \(_\)]\))/(
    
87. \!\(\*OverscriptBox[\(i1\), \(_\)]\) -
    
88. \!\(\*OverscriptBox[\(o\), \(_\)]\)))];
    
89. \!\(\*OverscriptBox[\(t1\), \(_\)]\) = Simplify[(
    
90. \!\(\*OverscriptBox[\(i1\), \(_\)]\) (i1 - o) - R1 Sqrt[ (i1 - o) (
    
91. \!\(\*OverscriptBox[\(i1\), \(_\)]\) -
    
92. \!\(\*OverscriptBox[\(o\), \(_\)]\))])/(i1 - o)];  (*套用公式*)
    
93. t1 = (2 (I v u + u + v - I))/(-w + I v (w + 1) + u (v + I) (w + 1) +
    
94.   3);
    
95. \!\(\*OverscriptBox[\(t1\), \(_\)]\) = (2 (-I v u + u + v + I) w)/(
    
96. 3 w - I v (w + 1) + u (v - I) (w + 1) - 1);    (* 人工协助简化结果 *)
    
97. Print["t1 = ", t1];
    
98. e = Simplify[ (u + v)/2 +
    
99.    I ((u^2 v^2 - u^2 - v^2 - 3)/(4 (u v + 1)) - R)];   
    
100. \!\(\*OverscriptBox[\(e\), \(_\)]\) =
     
101. Simplify[ (u + v)/2 -
     
102.    I ((u^2 v^2 - u^2 - v^2 - 3)/(4 (u v + 1)) - R)];
     
103. Print["e = ", e];
     
104. kT1K = Simplify[kf[t1, k]];  kKE = Simplify[kf[k, e]];
     
105. Print["T1K的复斜率 = ", kT1K]; Print["KE的复斜率 = ", kKE];
     
106. If[kT1K == kKE, Print["由于T1K的复斜率 = KE的复斜率，所以 T1、K、E 三点共线 "]]
     
107. t2 = Simplify[-((R2 Sqrt[ (i2 - o) (
     
108. \!\(\*OverscriptBox[\(i2\), \(_\)]\) -
     
109. \!\(\*OverscriptBox[\(o\), \(_\)]\))] + i2
     
110. \!\(\*OverscriptBox[\(o\), \(_\)]\) - i2
     
111. \!\(\*OverscriptBox[\(i2\), \(_\)]\))/(
     
112. \!\(\*OverscriptBox[\(i2\), \(_\)]\) -
     
113. \!\(\*OverscriptBox[\(o\), \(_\)]\)))];
     
114. \!\(\*OverscriptBox[\(t2\), \(_\)]\) = Simplify[(
     
115. \!\(\*OverscriptBox[\(i2\), \(_\)]\) (i2 - o) - R2 Sqrt[ (i2 - o) (
     
116. \!\(\*OverscriptBox[\(i2\), \(_\)]\) -
     
117. \!\(\*OverscriptBox[\(o\), \(_\)]\))])/(i2 - o)];(*套用公式*)  
     
118. t2 = -((2 I (u - I) (v - I))/(
     
119.   u (v + I) (w - 1) + I v (w - 1) - w - 3));
     
120. \!\(\*OverscriptBox[\(t2\), \(_\)]\) = (
     
121. 2 (-I v u + u + v + I) w)/(-I v (w - 1) + u (v - I) (w - 1) + 3 w +
     
122.   1);  (* 人工协助简化结果 *)
     
123. Print["t2 = ", t2];
     
124. kEP = Simplify[kf[e, p]];  kPT2 = Simplify[kf[p, t2]];
     
125. Print["EP的复斜率 = ", kEP]; Print["PT2的复斜率 = ", kPT2];
     
126. If[kT1K == kKE, Print["由于EP的复斜率 = PT2的复斜率，所以 E、P、T2 三点共线 "]]
     

复制代码

程序运行结果：

dlsh

TSC999 发表于 2021-12-17 15:10
下面用楼主的基本方法证明泰博定理。

“人工协助简化结果 ”需要进一步说明，相切判断与下图情况不完全符合。