最多五点圆数目

mathe

si2[1]=4d2-3
si2[2]=c
si2[3]=b-d
si2[4]=2a-1
si2[5]=5q+2
si2[6]=8r-5
si2[7]=8t-7
si2[8]=2s-7

poly gg0;
list l0;
l0=1,6,9,10;
gg0=inonecv(allnodes, l0);
l0=1,6,9,11;
poly gg1;
gg1=inonecv(allnodes, l0);
l0=2,5,8,10;
poly gg2=inonecv(allnodes, l0);
l0=2,5,8,11;
poly gg3=inonecv(allnodes, l0);
l0=3,4,7,10;
poly gg4=inonecv(allnodes, l0);
l0=3,4,7,11;
poly gg5=inonecv(allnodes, l0);


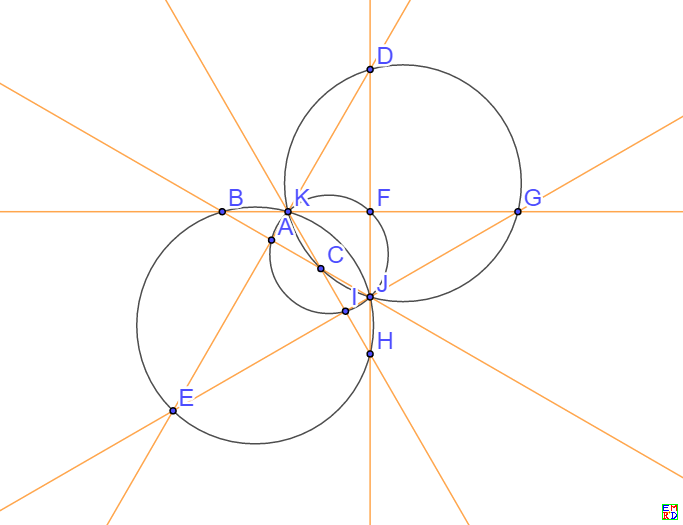
A=(0.16666666666666666666666666666666666667, -0.096225044864937627418191463416992909275)
B=(0,0)
C=(0.33333333333333333333333333333333333334, -0.19245008972987525483638292683398581855)
D=(0.50000000000000000000000000000000000000, 0.48112522432468813709095731708496454637)
E=(-0.16666666666666666666666666666666666667, -0.67357531405456339192734024391895036492)
F=(0.5,0)
G=(1,0)
H=(0.50000000000000000000000000000000000000, -0.48112522432468813709095731708496454637)
I=(0.41666666666666666666666666666666666667, -0.33678765702728169596367012195947518246)
J=(0.50000000000000000000000000000000000000, -0.28867513459481288225457439025097872782)
K=(0.22222222222222222222222222222222222222, 0)

（这个图看起来ECF似乎三点共线，但是实际上不是）
l5.38

mathe

si2[1]=256d8-2048d6-2272d4+132d2-99
si2[2]=66158c-768d6-4848d4+102824d2-743
si2[3]=9b+15c2d-46cd-d3+25d
si2[4]=2a-1
si2[5]=q+2c-1
si2[6]=3r-4c-4d2+1
si2[7]=12t-8r-4b2-8c-9
si2[8]=s-t+r

d=2.9970330578408152512282255822101745671
c=0.37563679478801637760685738593545931730
b=-0.28473323020327121686525130995531074751
a=0.5
q=0.24872641042396724478628522812908136540
r=12.143791926104911777113775353743162690
t=9.1233101513892817832569105424845792041
s=-3.0204817747156299938568648112585834858

A=(0.12436320521198362239314261406454068208, 0.30000119044923776018375491574765040345)
B=(0,0)
C=(-0.076860687770883950432996374381932000053, -0.18541093236305927165968015914291418595)
D=(0.40656920840921227845001544028987369128, 0.46070804419544096011217918414914798082)
E=(0.58098211021436108323073383777886032543, 0.56003034203565290531775033496154454526)
F=(0.46431261320812694733859408560177411621, 0)
G=(1,0)
H=(0.53093241362119590084315805435441437418, -0.53152871847232174324778458668732594619)
I=(2.0411733009790108977715904599837060952, -1.3915602509572124087492898373965208744)
J=(0.35651951181604709606243965686542774022, 0.86003153248489066550150525070919495178)
K=(-0.40244778596573514565227797689294536698, 0)


l5.33

mathe

52#的构图中还存在若干额外三点共线和四点共圆，所以如图，我们可以通过添加额外的粉红色点线或者再额外添加红色点线得到
13点11个五点圆和14点13个五点圆的构图。

mathe

stackexchange上Florian F指出，使用球极投影，我们可以将正20面体的12个顶点投影到平面上，从而形成12个点12个五点圆的构图。同样我们还可以将正12面体的20个顶点投影到平面上，从而形成20个顶点24个五点圆的构图。

mathe

Florian指出继续添加一个黑点和三条黑线可以增加一个点增加三圆, 有就是13点可以构成15个五点圆

而在上面基础上再加红点和三条红线可以得出14个点构成18个五点圆团。继续加粉色点和两条粉色线可以得到15个点构成20个五点圆