- 注册时间
- 2023-1-4
- 最后登录
- 1970-1-1
- 威望
- 星
- 金币
- 枚
- 贡献
- 分
- 经验
- 点
- 鲜花
- 朵
- 魅力
- 点
- 上传
- 次
- 下载
- 次
- 积分
- 74
- 在线时间
- 小时
|
马上注册,结交更多好友,享用更多功能,让你轻松玩转社区。
您需要 登录 才可以下载或查看,没有账号?欢迎注册
×
各位老师好,我是遥感方向的研究生,最近遇到一个本质上是数学统计的难题,限于个人数学水平有限不知道如何去证明。
下面是背景介绍,后面我会转换为纯数学问题。
卫星会定期拍摄影像(这里图1中为每隔12天),将影像分割成很多像元。
这里假设$x_i^j$表表示第$j$个像元的第$i$幅的影像指标A的值。比如$x_10^20=-5$表示第20个像元的第10幅影像的指标A为-5,
水稻的一个生长周期大约是半年,即$i≤20$。
图1

图1中可以清晰的看出,水稻的第1幅影像(这里指5月1日)的指标A大概率是-8,第2幅影像的指标A大概率是-13。
这里的指标A是专业术语,可以直接理解为类似高程的物理含义。
我的任务就是根据$x_i$的时间序列将$x^j$中的水稻区分出来。
物理上,水稻对比其他地物(将所有其他地物归类为非水稻)有2大特征,结合图1不难发现:
1.水稻的$x_i$变化幅度很大,非水稻的$x_i$变化幅度很小,这里的变化幅度可以理解为方差/极差。
2.水稻的$x_i$取最小值必定是在前3幅影像,对应图1中13-May左右,而非植物的$x_i$基本不随时间变化.
这里前3幅影像对应实际情况是插秧阶段,尽管同一区域的水稻种植肯定不是同一天,但是时间差异不会很大。
实际操作时像元个数很多,$x^j$有十万甚至百万,想象一下图1个各类的曲线分别左右、上下平移(平移范围不能太大)。
即所有的$x^j$,水稻和非水稻的散点图还是符合上面的2大特征的。
于是有个学者提出了一个方法,定义一个新的参数,对于每个像元$x^j$定义$z^j$为
$z^j$=$max(\frac{x_m-x_n}{x_m+x_n})$
式中$m>n$,$n$取1,2,3,$m$取遍所有$i$
结果发现$z^j$呈现高斯混合分布,两个高斯分布(分别对应水稻和非水稻)的交点求出来即是阈值,这样就可以进行分类
具体情况如图2.
图2
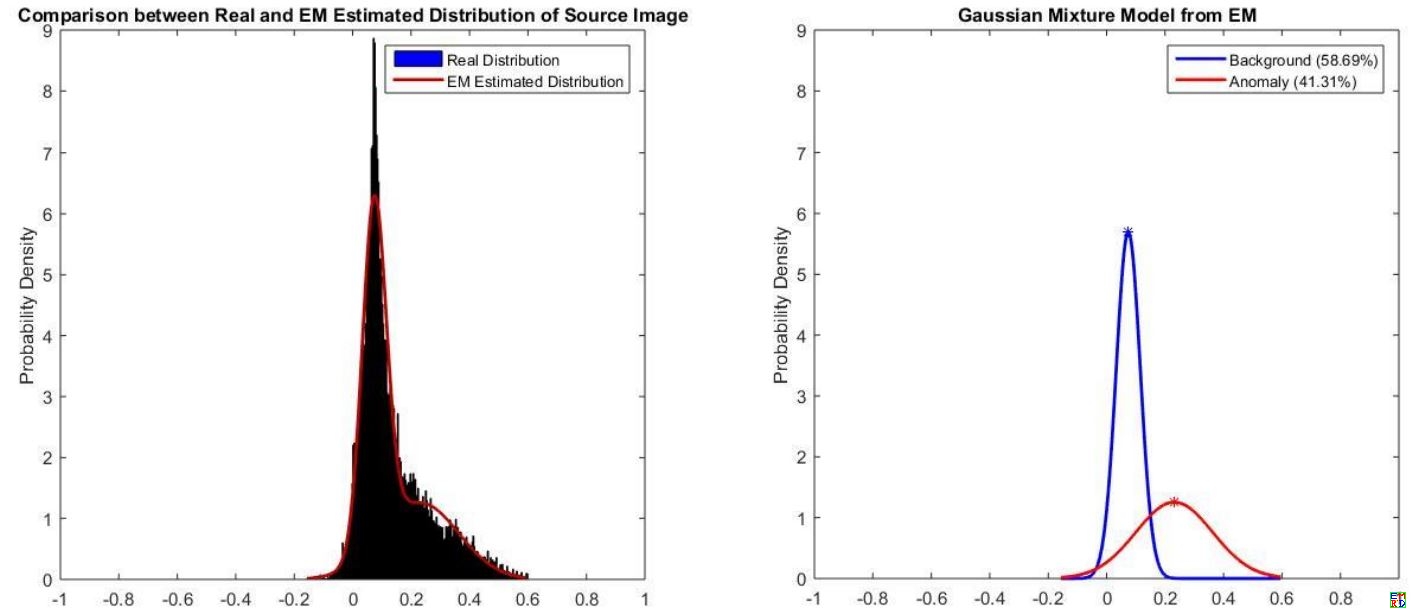

我进行了大量实验,发现每次实验结果都是符合高斯混合分布。
转化为数学问题就是:
$a_i^j$表表示第$j$个数列的第$i$个数,其中$i≤20$。
数列$a^j$包含T和S两种,满足:
1.T的$a_i$变化幅度很大,S的$a_i$变化幅度很小,这里的变化幅度可以理解为方差/极差。
2.T的$a_i$取最小值必定是在前3个数,而S的$a_i$最小值随机分布.
定义
$b^j$=$max(\frac{a_m-a_n}{a_m+a_n})$
式中$m>n$,$n$取1,2,3,$m$取遍所有$i$
则$b^j$呈现高斯混合分布,两个高斯分布(分别对应S和T)的交点求出来即是阈值,这样就可以进行分类。
我想知道为什么?如何证明这样处理必定会得到高斯混合分布。 |
评分
-
查看全部评分
|