三角形的Yff点

hejoseph

Yff点.pdf (66.43 KB, 下载次数: 22)

2023-3-4 15:15 上传

点击文件名下载附件

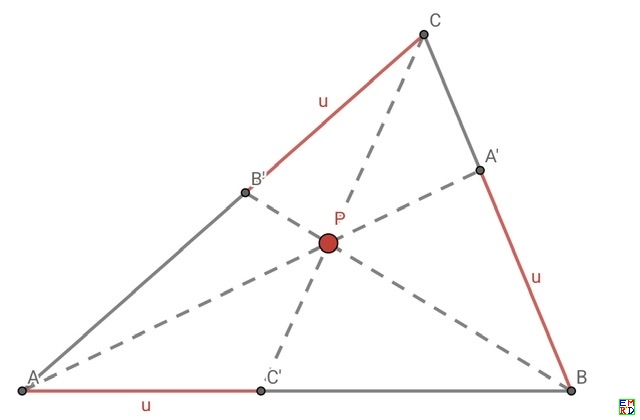
我们知道，三角形中奇妙的Brocard点与各顶点的连线将三角形的各内角分出相等的部分。上传的文档中我们化角为边，定义了从各边中截出相等部分的类Brocard点，缩记为Yff点。

Yff点：给定△ABC, 若投影中心P使得各顶点在对边的投影A', B', C'满足BA'=CB'=AC'或CA'=AB'=BC'，就称之为△ABC的Yff点。满足前式的称为正（向）Yff点，满足后式的称为负（向）Yff点。

记△ABC各边长为a, b, c，设各顶点透过Yff点在各边的投影截距为u，由Ceva定理可得方程\[
u^3+(u-a)(u-b)(u-c)=0
\]上传的文档通过分析这个三次方程研究了Yff点的性质，计算很复杂，不知道有没有简单的计算方法？
计算过程太长，不复发贴，有兴趣的请打开文档。


补充内容 (2023-3-10 17:49):
Yff其实是人名，全名是Peter Yff，这个点是1963年提出的，参考资料
https://mathworld.wolfram.com/YffPoints.html