- 注册时间
- 2023-3-12
- 最后登录
- 1970-1-1
- 威望
- 星
- 金币
- 枚
- 贡献
- 分
- 经验
- 点
- 鲜花
- 朵
- 魅力
- 点
- 上传
- 次
- 下载
- 次
- 积分
- 53
- 在线时间
- 小时
|
马上注册,结交更多好友,享用更多功能,让你轻松玩转社区。
您需要 登录 才可以下载或查看,没有账号?欢迎注册
×
自己发现的这个东西, 网上查了下"twined magic squares"及相关中文(中文网页信息污染太严重, 不是很容易查)没找到相关的.
不知道是不是还没有人发现过这东西?
-定义用语:
将0至(2^(2n+1))-1共2^(2n+1)个连续整数填入<两个>长宽2^n的方块格中,
且使方块格纵, 横, 对角线(及泛对角线?)相加皆等于幻和, 我称这两个方块格为<对偶幻方>.
计算幻和(javascript代码, 下同):
- function oddsq_sum(level)
- {
- return ((1<<level)-1)<<((level-2)-(level>>1));
- }
oddsq_sum(5) = 62, oddsq_sum(7) = 508.
令k=2n+1, k=5的这种幻方为:
- 0 30 29 3
- 27 5 6 24
- 7 25 26 4
- 28 2 1 31
- ----------
- 16 14 13 19
- 11 21 22 8
- 23 9 10 20
- 12 18 17 15
k=7的这种幻方为:
- 0 126 125 3 4 122 121 7
- 119 9 10 116 115 13 14 112
- 111 17 18 108 107 21 22 104
- 24 102 101 27 28 98 97 31
- 96 30 29 99 100 26 25 103
- 23 105 106 20 19 109 110 16
- 15 113 114 12 11 117 118 8
- 120 6 5 123 124 2 1 127
- ----------
- 64 62 61 67 68 58 57 71
- 55 73 74 52 51 77 78 48
- 47 81 82 44 43 85 86 40
- 88 38 37 91 92 34 33 95
- 32 94 93 35 36 90 89 39
- 87 41 42 84 83 45 46 80
- 79 49 50 76 75 53 54 72
- 56 70 69 59 60 66 65 63
-构造法(代码):
基于xor(基于xor的幻方构造法我也没在网上看到过类似的), 完整代码见附件mgsq.js.txt
另mkmgsq_even()是构造偶数2n阶的, 同样基于xor.
 mgsq.js.txt
(4.34 KB, 下载次数: 0)
mgsq.js.txt
(4.34 KB, 下载次数: 0)
- function mkmgsq_odd(level)
- {
- var retsq0=uintsqarr_withp(level);
- var retsq1=uintsqarr_withp(level);
- allrg=1<<(level);
- sqrg=1<<(level-1);
- var lztidx=allrg-1;
- var hfallrg=allrg>>2;
- var odd_hf=level>>1;
- var i=0;
-
- for(var tk0=0;tk0<2;tk0++)
- {
- for(var tk1=0;tk1<hfallrg;tk1++){
- var tztchg=(i^(i>>odd_hf));
- tztchg = (tztchg^(tztchg>>1))&1;
- var rvidx=lztidx-i;
- if(tztchg == 1){
- retsq0[i]=rvidx;
- retsq0[rvidx-sqrg]=i;
- } else {
- retsq0[i]=i;
- retsq0[rvidx-sqrg]=rvidx;
- }
- i++;}
- var tmp=retsq0;
- retsq0=retsq1;
- retsq1=tmp;
- }
- return [retsq0,retsq1];
- }
printmgsq_by4(mkmgsq(5))
或
printmgsq_by4(mkmgsq(11))
-<对偶幻方>的性质:
称对偶幻方中的第一个为A[y,x], 第二个为B[y,x], 以k=5为例,
A与B的平均为:
- 8 22 21 11
- 19 13 14 16
- 15 17 18 12
- 20 10 9 23
(A[2,1]+B[2,1])/2 = (25+9)/2 = 17
.etc
可发现平均阵的1, 2, 3, 4行为B[y,x]阵2, 1, 4, 3行的左右逆,
即平均阵为B[y,x]阵的<分半逆旋>.
以个人经验, 这种<分半逆旋>在二进制xor运算图样中很常见.
将A[y,x]的<分半逆旋>与B[y,x]的<分半逆旋>取平均, 则又回到A[y,x]与B[y,x].
-定性A[y,x]与B[y,x]:
周知, 令k=4, 在0至15这十六个数字中, 将有<全0>("全阴爻")与<全1>("全阳爻")的二进制数字各一个(0和15),
<一1三0>的数字四个(1, 2, 4, 8), <三1一0>的数字四个(7, 11, 14, 13),
其余六个二进制数字为<二1二0>, 即按照组合系数1-4-6-4-1来分组的.
我用颜色在一个右转45度的(非对偶)四阶幻方上标出这五组数字(<全0>与<全1>同为灰色), 得到:
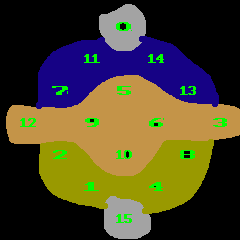
( 0+14+13+3 = 14+5+9+2 = 0+5+10+15 = 30 )
可发现这些数字组在幻方上的分布应该是看起来平衡的.
於是, 当k=5, 我同样在<对偶幻方>上标出1-5-10-10-5-1这六组:

可见A[y,x]与B[y,x]虽各自看起来仍平衡, 但AB的图样却是不同的, A较B的图样, 更为接近偶数的非对偶幻方.
於是, 我称A阵为"本根", B阵为"派生".
这样的定性与我另外一个发现相关: 属A组的数与属B组的数在<16宫派生32宫>(即(2^4)^2派生(2^5)^2; 256各生四, 派生1024)上的图样及作用是不同的,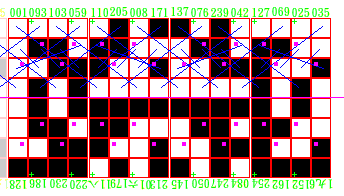

这另一个发现还待整理.
|
|