证明 E、G 两个交点的坐标都是定值

TSC999

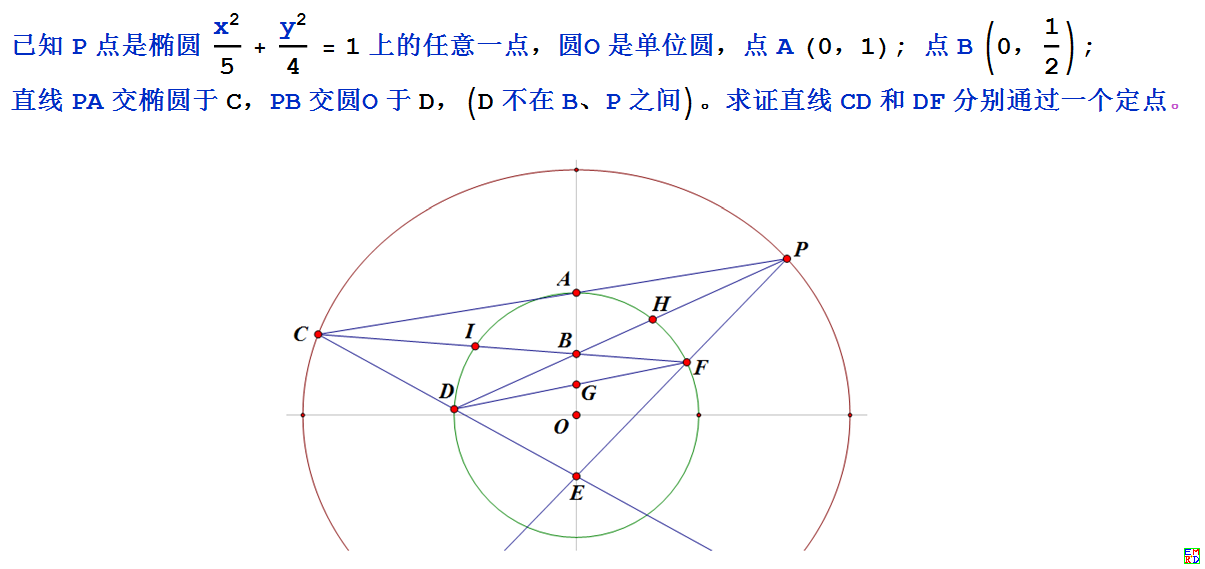
这个题用复平面上的解析几何做是非常简单的。构图和设点方法为：设圆 O 为单位圆，圆心在坐标系原点。
H 点的坐标设为变量，令 H 点的坐标为 \(h=u+i v\)，由于 H 在单位圆上，故 H 点的共轭坐标为 \(\overline{h}=1/h\) 。由此可求出\(BH\)线与圆O及椭圆的交点\(D\)、\(P\)的坐标。然后再算出\(PA\) 线与椭圆的交点 \(C\) 的坐标。继续算出\(CB\) 线与圆O的交点 \(F\) 的坐标。最后算出\(CD\) 与\(PF\) 线的交点\(E\)以及\(DF\) 线与\(OB\) 线的交点\(G\) 的坐标。
结果是 \(E\) 点坐标和 \(G\) 点坐标都是常数，都与 \(H\) 点的坐标无关。
在程序中点的名称都用大写字母表示，点的复数坐标都用小写字母表示。小写字母上加一横线表示其共轭复数。在这个计算体系中，点的坐标算出后，往往需要同时算出它的共轭复数。
用 mathematica 写的程序：

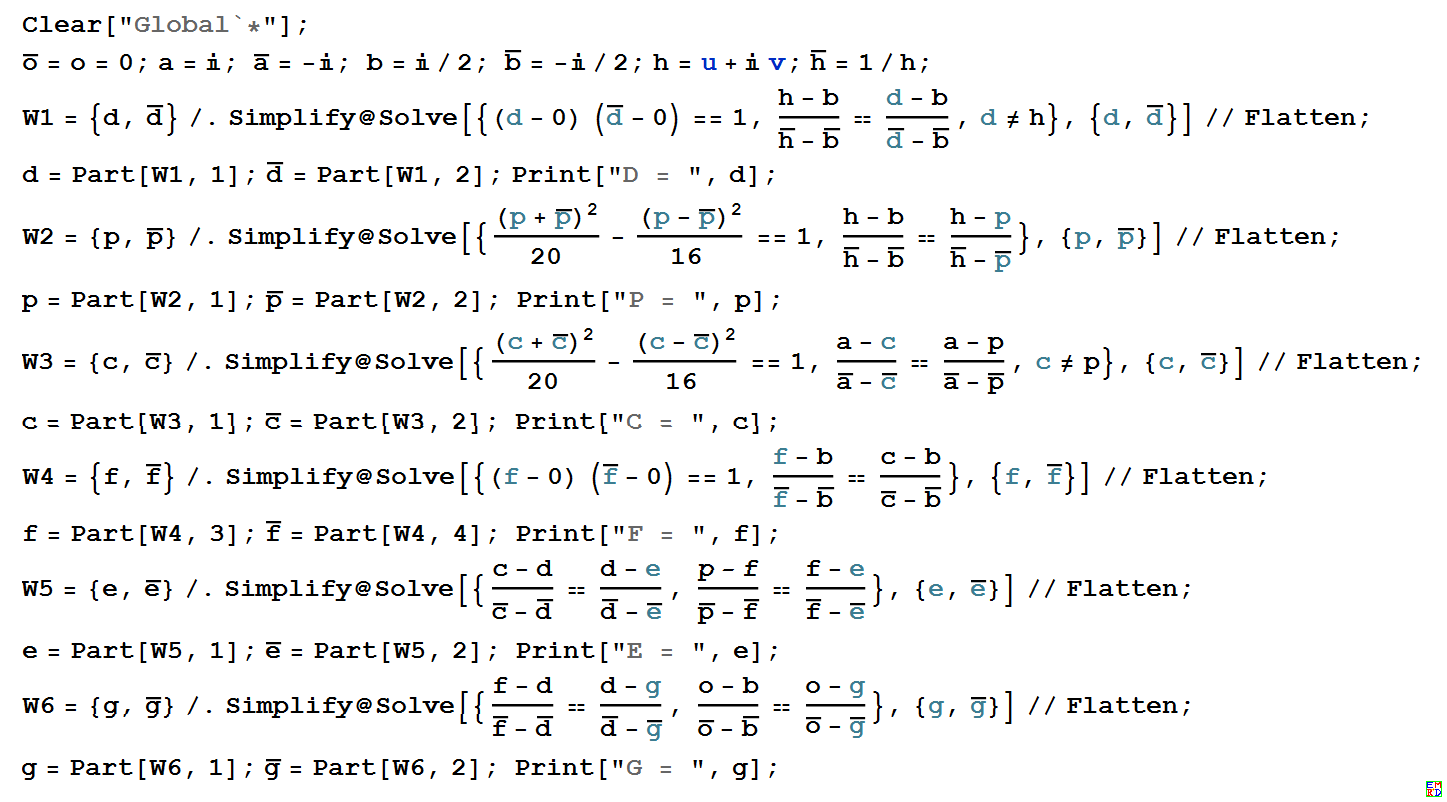
程序运行结果：

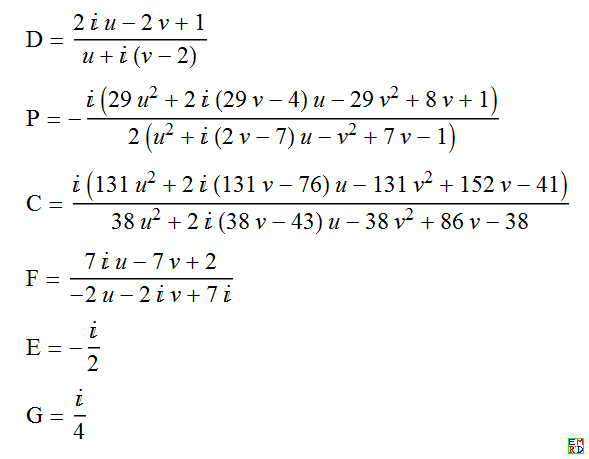
程序代码：

1. Clear["Global`*"];
   
2. \!\(\*OverscriptBox[\(o\), \(_\)]\) = o = 0; a = I; \!\(\*OverscriptBox[\(a\), \(_\)]\) = -I; b = I/2;
   
3. \!\(\*OverscriptBox[\(b\), \(_\)]\) = -I/2; h = u + I v; \!\(\*OverscriptBox[\(h\), \(_\)]\) = 1/h;
   
4. W1 = {d, \!\(\*OverscriptBox[\(d\), \(_\)]\)} /. Simplify@Solve[{(d - 0) (\!\(\*OverscriptBox[\(d\), \(_\)]\) - 0) == 1, (h - b)/(\!\(\*OverscriptBox[\(h\), \(_\)]\) - \!\(\*OverscriptBox[\(b\), \(_\)]\)) == (d - b)/(\!\(\*OverscriptBox[\(d\), \(_\)]\) - \!\(\*OverscriptBox[\(b\), \(_\)]\)), d != h}, {d, \!\(\*OverscriptBox[\(d\), \(_\)]\)}] // Flatten;d = Part[W1, 1];
   
5. \!\(\*OverscriptBox[\(d\), \(_\)]\) = Part[W1, 2]; Print["D = ", d];
   
6. W2 = {p, \!\(\*OverscriptBox[\(p\), \(_\)]\)} /. Simplify@Solve[{(p + \!\(\*OverscriptBox[\(p\), \(_\)]\))^2/20 - (p - \!\(\*OverscriptBox[\(p\), \(_\)]\))^2/16  == 1, (h - b)/(\!\(\*OverscriptBox[\(h\), \(_\)]\) - \!\(\*OverscriptBox[\(b\), \(_\)]\)) == (h - p)/(\!\(\*OverscriptBox[\(h\), \(_\)]\) - \!\(\*OverscriptBox[\(p\), \(_\)]\))}, {p, \!\(\*OverscriptBox[\(p\), \(_\)]\)}] // Flatten;
   
7. p = Part[W2, 1]; \!\(\*OverscriptBox[\(p\), \(_\)]\) = Part[W2, 2]; Print["P = ", p];
   
8. W3 = {c, \!\(\*OverscriptBox[\(c\), \(_\)]\)} /. Simplify@Solve[{(c + \!\(\*OverscriptBox[\(c\), \(_\)]\))^2/20 - (c -
   
9. \!\(\*OverscriptBox[\(c\), \(_\)]\))^2/16  == 1, (a - c)/(\!\(\*OverscriptBox[\(a\), \(_\)]\) - \!\(\*OverscriptBox[\(c\), \(_\)]\)) == (a - p)/(\!\(\*OverscriptBox[\(a\), \(_\)]\) - \!\(\*OverscriptBox[\(p\), \(_\)]\)), c != p}, {c, \!\(\*OverscriptBox[\(c\), \(_\)]\)}] // Flatten;
   
10. c = Part[W3, 1]; \!\(\*OverscriptBox[\(c\), \(_\)]\) = Part[W3, 2]; Print["C = ", c];
    
11. W4 = {f, \!\(\*OverscriptBox[\(f\), \(_\)]\)} /. Simplify@Solve[{(f - 0) (\!\(\*OverscriptBox[\(f\), \(_\)]\) - 0) == 1, (f - b)/(\!\(\*OverscriptBox[\(f\), \(_\)]\) - \!\(\*OverscriptBox[\(b\), \(_\)]\)) == (c - b)/(\!\(\*OverscriptBox[\(c\), \(_\)]\) - \!\(\*OverscriptBox[\(b\), \(_\)]\))}, {f, \!\(\*OverscriptBox[\(f\), \(_\)]\)}] // Flatten;
    
12. f = Part[W4, 3]; \!\(\*OverscriptBox[\(f\), \(_\)]\) = Part[W4, 4]; Print["F = ", f];
    
13. W5 = {e, \!\(\*OverscriptBox[\(e\), \(_\)]\)} /. Simplify@Solve[{(c - d)/(\!\(\*OverscriptBox[\(c\), \(_\)]\) - \!\(\*OverscriptBox[\(d\), \(_\)]\)) == (d - e)/(\!\(\*OverscriptBox[\(d\), \(_\)]\) - \!\(\*OverscriptBox[\(e\), \(_\)]\)), (p - f)/(\!\(\*OverscriptBox[\(p\), \(_\)]\) - \!\(\*OverscriptBox[\(f\), \(_\)]\)) == (f - e)/(\!\(\*OverscriptBox[\(f\), \(_\)]\) - \!\(\*OverscriptBox[\(e\), \(_\)]\))}, {e,
    
14. \!\(\*OverscriptBox[\(e\), \(_\)]\)}] // Flatten;
    
15. e = Part[W5, 1]; \!\(\*OverscriptBox[\(e\), \(_\)]\) = Part[W5, 2]; Print["E = ", e];
    
16. W6 = {g, \!\(\*OverscriptBox[\(g\), \(_\)]\)} /. Simplify@Solve[{(f - d)/(\!\(\*OverscriptBox[\(f\), \(_\)]\) - \!\(\*OverscriptBox[\(d\), \(_\)]\)) == (d - g)/(\!\(\*OverscriptBox[\(d\), \(_\)]\) - \!\(\*OverscriptBox[\(g\), \(_\)]\)), (o - b)/(\!\(\*OverscriptBox[\(o\), \(_\)]\) - \!\(\*OverscriptBox[\(b\), \(_\)]\)) == (o - g)/(\!\(\*OverscriptBox[\(o\), \(_\)]\) - \!\(\*OverscriptBox[\(g\), \(_\)]\))}, {g, \!\(\*OverscriptBox[\(g\), \(_\)]\)}] // Flatten;
    
17. g = Part[W6, 1]; \!\(\*OverscriptBox[\(g\), \(_\)]\) = Part[W6, 2]; Print["G = ", g];

复制代码

TSC999

不知道用纯几何方法和传统平面解析几何（即笛卡尔平面解析几何）的方法如何做这道题？

期待大神赐教。

nyy

你的代码简直是惨不忍睹！难道你自己就没觉得难受过吗？
一句注释都没有！也没缩进！

nyy

OverBar[z]，这个会不会比你的好一些？

nyy

你这个用画图的办法最简单！
先给一个H1点，再给一个H2点，如果有这些过定点，那么这直线肯定过两次形成的交点！

nyy

TSC999 发表于 2023-3-21 11:01
不知道用纯几何方法和传统平面解析几何（即笛卡尔平面解析几何）的方法如何做这道题？

期待大神赐教。

代码要有注释，有缩进，然后不要一个代码很长很长

要不然以后你自己都看不懂自己的代码了！

mathe

这道题目本质上是一道射影几何问题，

如上图，给定圆锥曲线$\Gamma$和定直线AB上三个点A,B,E
对于$\Gamma$上动点C, CA交$\Gamma$于另外一个点P,那么PB和CE的交点D的轨迹是一条圆锥曲线。


我们可以通过射影变换，将$\Gamma$变换为一个圆而且同时将A点变换为这个圆的圆心，于是AEB是圆的一条固定的直径。
CP是一条动直径，而且BC和EP交于动点D,如果我们能够证明D点的轨迹是一个圆，就可以证明这个问题了（下面这个图和

在这个图上用射影几何证明比较清晰，我们假设E关于A点的对称点为E'，那么当C点移动时，由于线束BC和E'C的交点轨迹是一个圆（圆锥曲线，二次点列），所以它们确定了一个从线束BC到E'C的射影变换（一次线束），由于E'C到EP是关于A点的中心对称变换，是一个特殊的射影变换，所以从BC到EP也确定了一个射影变换，于是直线BC和EP的交点必然也是圆锥曲线（二次点列，但是这个方法没有说明是圆），从而证明了原图中的命题。

nyy

免费帮你改进改进代码：

1. Clear["Global`*"];(*Clear all variables*)
   
2. (*子函数,用来计算a、b这两个复数对应的斜率(其实得到的是过ab两点的直线的倾角的两倍)*)
   
3. slope[a_,b_]:=((a-b)/(OverBar[a]-OverBar[b]))
   

复制代码

这个是个子函数，用来给你缩短你的程序，代码来源

https://bbs.emath.ac.cn/forum.ph ... 4&fromuid=14149

1. Clear["Global`*"];(*Clear all variables*)
   
2. (*子函数,用来计算a、b这两个复数对应的斜率(其实得到的是过ab两点的直线的倾角的两倍)*)
   
3. slope[a_,b_]:=((a-b)/(OverBar[a]-OverBar[b]))
   
4. (*子函数,用来判定三点是否共线,如果共线,返回True,否则False*)
   
5. sdgx[a_,b_,c_]:=If[slope[a,b]==slope[b,c],True,False]
   

复制代码

进一步化简代码

1. Clear["Global`*"];(*Clear all variables*)
   
2. (*子函数,用来计算a、b这两个复数对应的斜率(其实得到的是过ab两点的直线的倾角的两倍)*)
   
3. slope[a_,b_]:=((a-b)/(OverBar[a]-OverBar[b]))
   
4. (*子函数,用来判定三点是否共线,如果共线,返回True,否则False*)
   
5. sdgx[a_,b_,c_]:=If[slope[a,b]==slope[b,c],True,False]
   
6. (*子函数,用来判定三点是否共线,三个复数点,先得到实数虚数部分,然后形成3*3的行列式,如果行列式结果等于零,则共线,否则不共线*)
   
7. sdgx2[a_,b_,c_]:=Det[Append[ComplexExpand@ReIm[#],1]&/@{a,b,c}]
   

复制代码

nyy

这题直接用平面解析几何，不用复数会如何？难道直接解析几何比用复数更难？