这些函数求极值的问题都是坑或者所谓的钓鱼贴吗？

yuange1975

#极值#  #钓鱼贴#

这些函数求极值的问题都是坑或者所谓的钓鱼贴吗？


现在一些地方流行问别人一些有点难度的求极值的问题，有些人会认为是坑是钓鱼贴。
这些问题基本上都是主要表现在导数是一个高次多项式方程，求根比较困难。

3次、4次多项式方程的话根表达式非常复杂，再带入原式计算，要么几乎不可能要么就是结果非常难看。如果大于等于5次，多项式又不能分解的话，那么就根表达式都不能得到，更别说得到根再求原式了。一般都是用数值解法了。


其实这里很多人没有转过一个弯。

我们得到导数多项式方程f(x)=0，求根困难的话，可以把原式y=g(x)再转换成一个方程h(y)=0。这样y=g(x)的值就可以用新的方程多项式测试大小，迭代等等计算了。

g(x)可以用除f(x)得到余项多项式G(x)，然后再用G(x)的和f(x)同次的待定系数多项式，除以f(x)，得到余项多项式恒等于0，就是余项多项式的每次系数都等于0，解出系数。

这样就得到h(y)=0的方程了。就可以用 h(y)得到y的大小情况等做分析了，用多项式的值大于小于0结合图形，就可以判断新方程根的大小，也就是对于极值大小做界限判定。以及可以迭代得到各个数值解等。


比如一道所谓的钓鱼贴。

http://tieba.baidu.com/p/8059710131?&share=9105&fr=sharewise&is_video=false&unique=085443DF1FC6C508549A22365B299B80&st=1692408515&client_type=1&client_version=12.45.7.0&sfc=copy&share_from=post


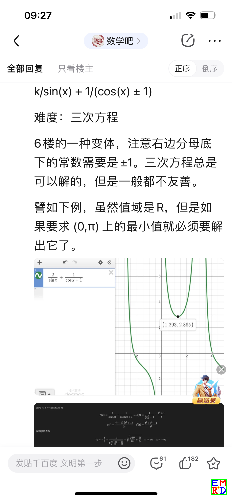
求F(x)=2/sin(x)+1/(cos(x)+1)的最小值，x区间(0,pi)。

换元，y=(t+2)(t^2+1)/(2t)

导数得到3次多项式方程：

t^3+t^2-1=0

现在就是3次方程，有唯一实根，求这个根下面的原式表达式。表达式非常复杂，写出来都麻烦更别说化简了。


下面我们按前面的转换思路来计算。

y=(t+2)(t^2+1)/(2t)
=(t^3+2t^2+t+2)/(2t)
=(3t^3+4t^2+t)/(2t)
=3/2*t^2+2t+1/2



2y的待定系数方程：

(3*t^2+4*t+1)^3+a*(3*t^2+4*t+1)^2+b*(3*t^2+4*t+1)+c-(t^3+t^2-1)*(27*t^3+81*t^2+(9*a+90)*t+15*a+73)

= (3*b+7*a+65)*t^2+(4*b+17*a+102)*t+c+b+16*a+74

上面要恒等于0，得到三元一次方程组：

(3*b+7*a+65)=0
(4*b+17*a+102)=0
c+b+16*a+74=0

解得：

a = -2,b = -17,c = -25

这样就得到原式方程：

8*y^3-8*y^2-34*y-25=0

解得最小值表达式为：
y = (23^(3/2)/(16*3^(3/2))+997/432)^(1/3)+55/(36*(23^(3/2)/(16*3^(3/2))+997/432)^(1/3))+1/3

数值解为
y = 2.8645……。

原贴里面的表达式没有化简非常复杂，算不上是一个成功的结果。这种表达式我也不知道怎么化简。

我们经过多项式方程的转换，这么得到的结果，正常的三次方程根的表达式结果，也不是怎么复杂，完全可以接受。

对于3次方程，如果只有一个实根，盛金公式的表达式都不算太复杂，都是传统的二三次开方的表达式。但是这个表达式再去做多项式计算，就比较复杂也不知道怎么化简了。我们改变了策略，先进行多项式的计算，这样都是一些简单的多项式乘除法运算了。这样就可以得到极值的方程式了。如果有再有需求，可以最后再去求根，这样就能得到相对漂亮简约的表达式了。


上面的h(y)方程转换方法都是基本的初、高中就能掌握的方法，不存在什么高深知识，只是计算量的问题。

这个计算可以借助工具
https://zh.numberempire.com/simplifyexpression.php 表达式化简工具。

(3*t^2+4*t+1)^3+a*(3*t^2+4*t+1)^2+b*(3*t^2+4*t+1)+c-(t^3+t^2-1)*(27*t^3+81*t^2+(9*a+90)*t+15*a+73)

这个商可以根据最后表达式结果的最高项除以f(x)的最高次得到，一步步加上去。用这个工具就很简单几步就出来了。
最后解多元1次方程组也可以在这网站里用工具直接得到。


当然如果f(x)是更高次方程，h(y)也会是更高次方程，可能没有解析解出来。但是有了这方程，也可以方便的判断界限等。


所以不要随便什么问题就说是坑是钓鱼贴，有时候可能是思路没有跟上。


欢迎加入知识星球《袁哥的技术天地》，大量的数学知识，数学题的新解题思路，一些问题的推广通解。知识星球里还有网络安全、投资等知识分享。

著名的鸭子共圆弧概率问题，网络名人李永乐老师都说太复杂解不出来。我的一篇知识星球分享里，理解和抓住问题本质，扩展到新空间里，就是一高纬几何的“体积”切割问题，直接显然的结果，直接得到答案。

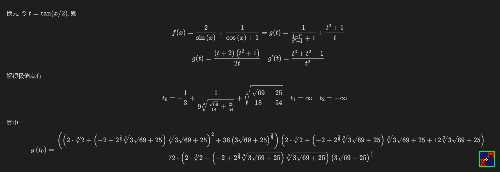
ShuXueZhenMiHu

图片有病毒。

yuange1975

图片一般不会有病毒，有些可能会利用漏洞，打开图片后利用漏洞植入代码执行。现在漏洞都是高价值武器，一般人根本不值得别人用这样的漏洞来攻击。 我本人也算是研究漏洞的专家吧，对这方面还算很熟悉。不要误导人。